Система отсчета. Кинематика материальной точки. Траектория и путь. Перемещение, скорость и ускорение материальной точки.
Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение каких-либо материальных точек или тел
Тело, относительно которого рассматривается движение других тел, называют телом отсчёта. Тело, размерами и формой которого можно пренебречь, в сравнении с масштабами движений, считают материальной точкой.
Положение материальной точки в пространстве в данный момент времени может быть задано:
а)радиус-вектором
соединяющим начало системы координат
с точкой М пространства, в которой в
данный
момент находится м. т.;
б) координатами точки М: х, у, z
Поскольку всякое движение происходит в пространстве и времени, то положение материальной точки в любой момент времени относительно тела отсчёта известно, если заданы её координаты
х = х(t), y = y(t), z = z(t) (1)
или радиус-вектор
(2)
Уравнения (1) и (2) называют кинематическими уравнениями движения материальной точки. Из анализа уравнений (1) и (2) следует, что закон движения материальной точки описывается тремя скалярными
уравнениями или одним векторным. уравнения (1) и (2) характеризуют движение одной и той же материальной точки, то между ними существует связь:
(3)
Длина радиус-вектора
(4)
где
–
единичные векторы (орты) осей координат.
Положение
материальной точки или тела в пространстве
можно характеризовать координатами x,
y,
z,
т. е. материальная точка может совершать
три независимых движения. Число
независимых координат, которые полностью
определяют положение тел (м. т.) в
пространстве, называют числом
степеней
свободы.
Общее
число степеней свободы молекулы
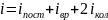(5)
Если м. т. совершает колебательное движение, то непрерывно происходит превращение кинетической энергии в потенциальную энергию и, наоборот, потенциальной – в кинетическую, поэтому число колебательных степеней свободы удваивается. Траектория – это воображаемая линия, по которой движется материальная точка.
Изменение
положения материальной точки в
пространстве при ее движении характеризуют
вектором перемещения
.
Вектор, проведённый из начального положения материальной точки в конечное, называют вектором перемещения.
Вектор
перемещения характеризует изменение
радиус-вектора движущейся точки за
рассматриваемый промежуток времени. В
течение промежутка времени ∆t материальная
точка переходит из точки 1 с координатами:
,
в точку 2 с координатами:
.
Вектор
перемещения материальной точки записывают
в виде
(6)
Если
материальная точка (тело) одновременно
участвует в нескольких перемещениях,
то, согласно принципу независимости
движений, каждое совершается независимо
одно от другого, т. е. выполняется закон
сложения векторов перемещений
Длина пути – скалярная величина, равна длине участка траектории, пройденного м. т. за рассматриваемый промежуток времени. Перемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени
Вектором средней скорости называют физическую величину, равную отношению вектора перемещения (приращению радиус-вектора) к промежутку времени, за которое это перемещение произошло. Вектор среднего ускорения равен отношению вектора изменения скорости к промежутку времени, за которое это изменение произошло.
Вектор мгновенной скорости равен пределу отношения приращения радиус-вектора м. т. к тому промежутку времени, за которое это приращение произошло, когда ∆t → 0 или равен первой производной радиус-вектора по времени.
Ускорение – быстрота изменения скорости.
Вектор среднего ускорения равен отношению вектора изменения скорости к промежутку времени, за которое это изменение произошло. Вектор мгновенного ускорения равен пределу отношения вектора изменения скорости к тому промежутку времени, когда ∆t → 0 или равен первой производной вектора скорости по времени или равен второй производной радиус- вектора по времени.