Индексы переменного и фиксированного составов. Индекс структурных сдвигов.

В экономическом анализе исследуется изменение во времени (или пространстве) средней величины индексируемого показателя, которая складывается как под влиянием значений показателя у индивидуальных элементов (единиц), из которых состоит объект, так и под влиянием соотношения их весов («структуры» объекта).

Если любой качественный индексируемый показатель обозначить через х, а его веса — через - f, то динамику среднего показателя можно отразить как за счет изменения обоих факторов (х и f), так и за счет каждого фактора отдельно. В результате получим три различных индекса:

• индекс переменного состава;

• индекс фиксированного состава;

• индекс структурных сдвигов.

Индекс переменного состава отражает динамику среднего показателя (для однородной совокупности) за счет изменения индексируемой величины х у отдельных элементов (частей целого) и за счет изменения весов f, по которым взвешиваются отдельные значения х. Любой индекс переменного состава — это отношение двух средних величин для однородной совокупности (за два периода или по двум территориям).

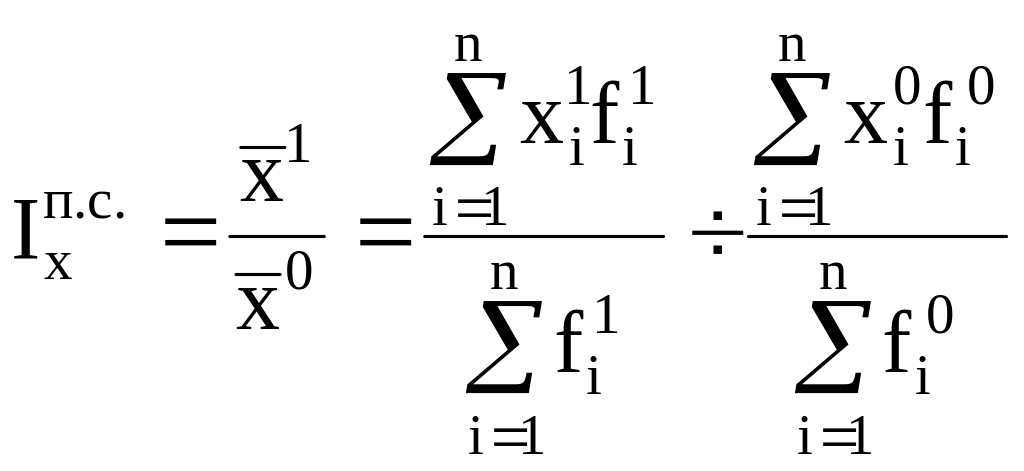
Индекс фиксированного состава отражает динамику среднего показателя лишь за счет изменения индексируемой величины х, при фиксировании весов на уровне отчетного периода f₁.

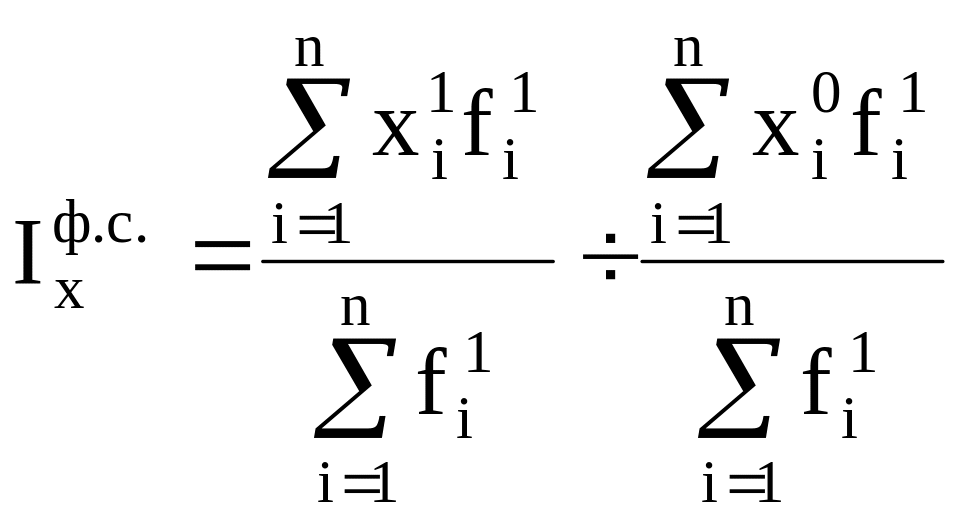
Динамику среднего показателя лишь за счет изменения весов f при фиксировании индексируемой величины на уровне базисного периода х₀ характеризуют индексом структурных сдвигов.

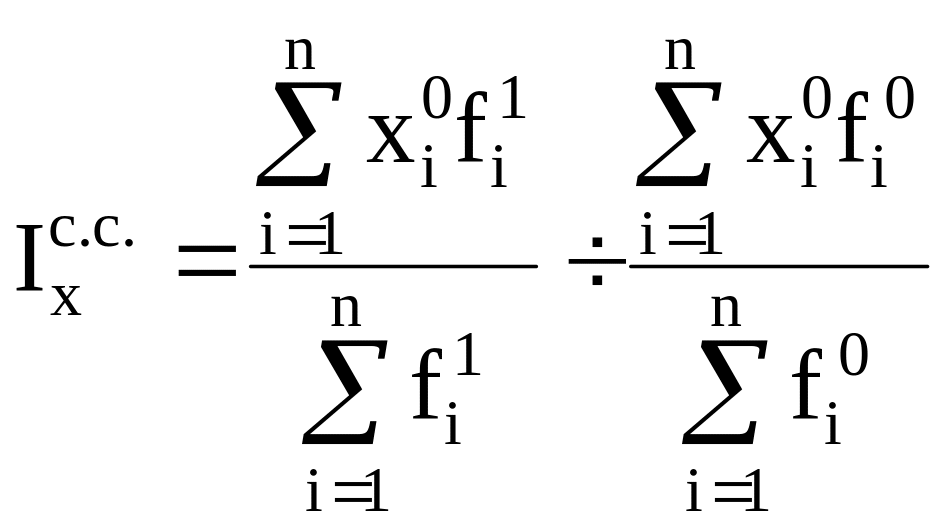
Индекс переменного состава есть произведение индекса фиксированного состава на индекс структурных сдвигов.

Динамику средних цен можно представить:

Индекс переменного состава, характеризует изменение средней цены под действием двух факторов: индивидуальной цены и структуры объёма продукции.

Индекс фиксированного состава, характеризует изменение средней цены под действием индивидуальной цены.

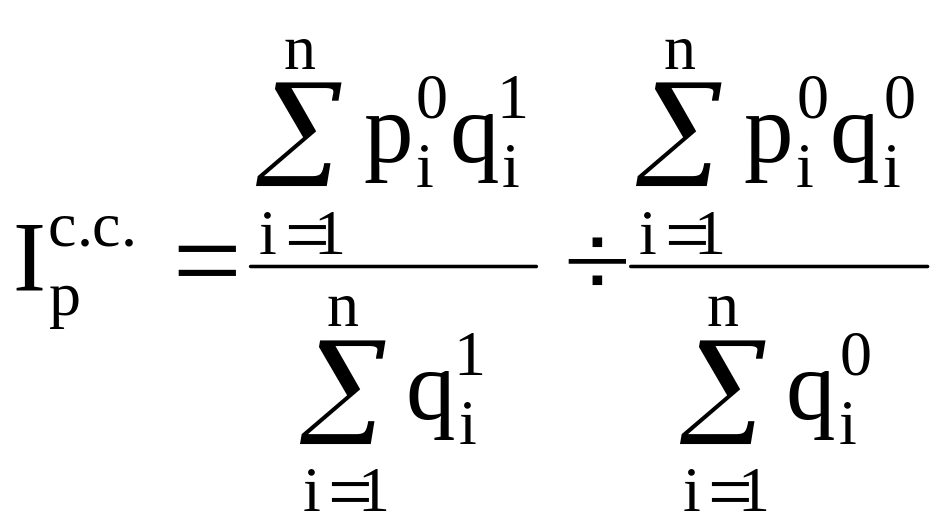Индекс структурных сдвигов, характеризует изменение средней цены под действием структуры объёма продукции.

Цепные и базисные индексы.

Цепные индексы получают при сопоставлении показателя любого периода с показателем предшествующего периода.

Цепные индексы физического объёма продукции:

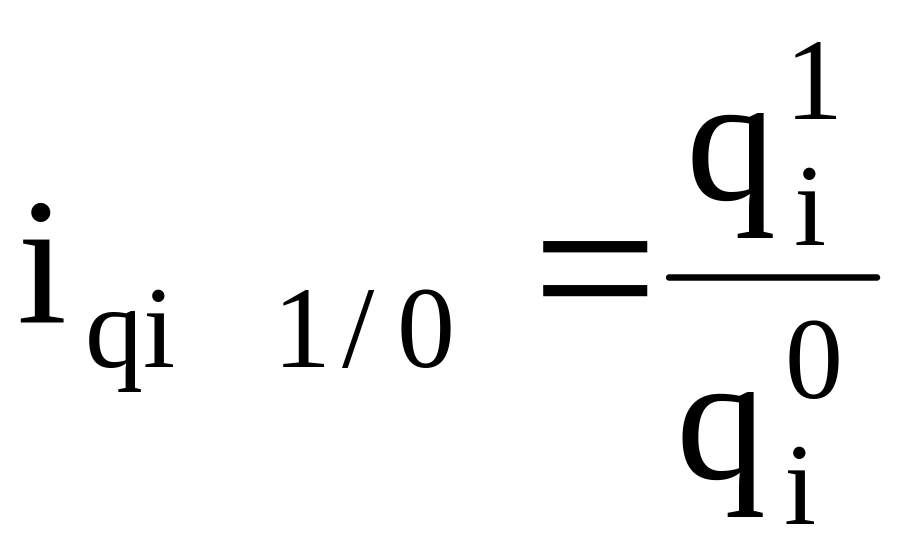
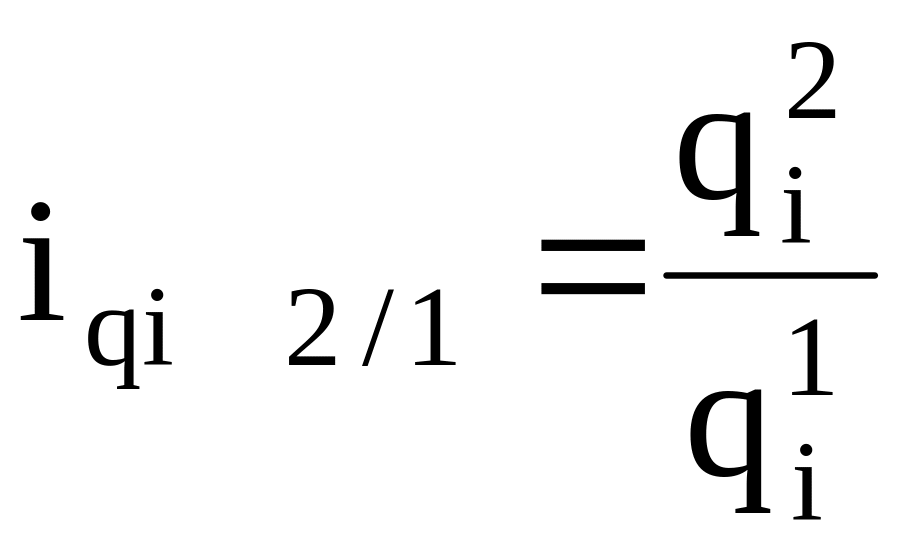
• индивидуальные: и т.д.

• агрегатные

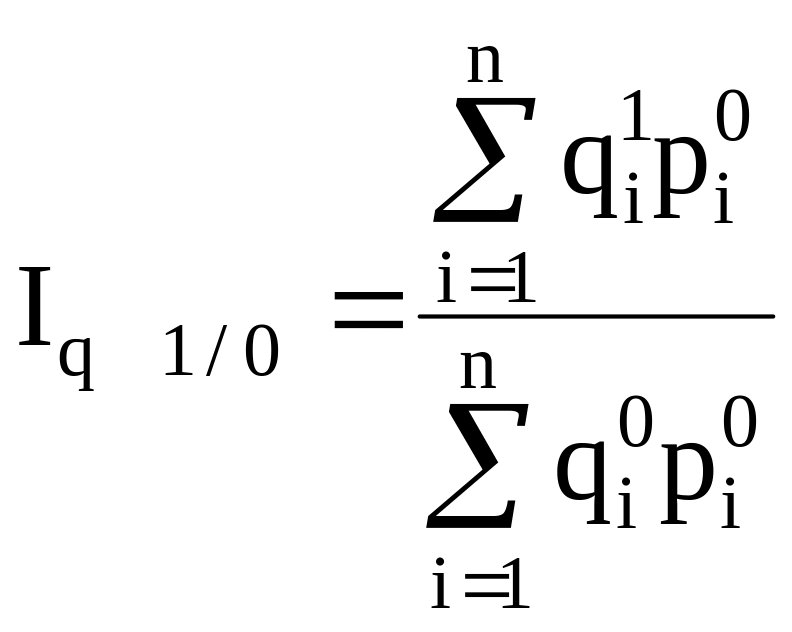
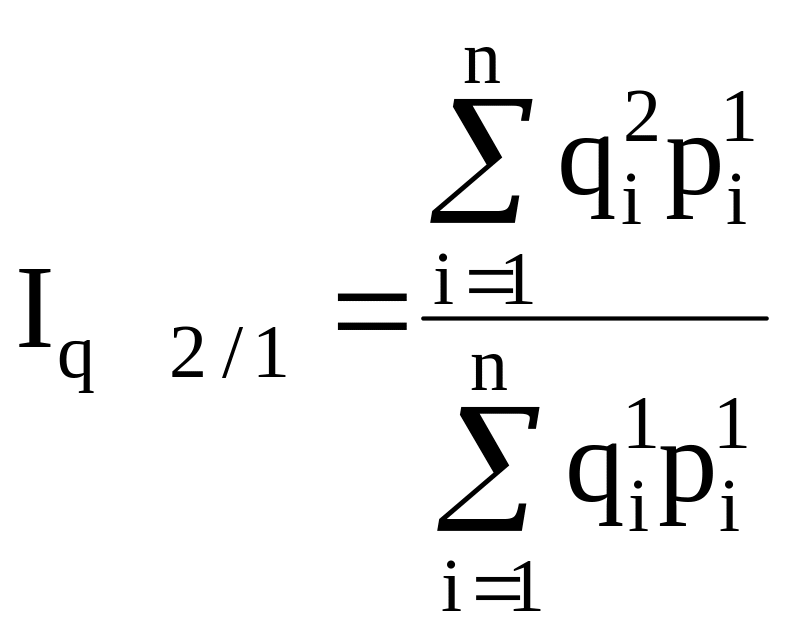
- с переменными весами 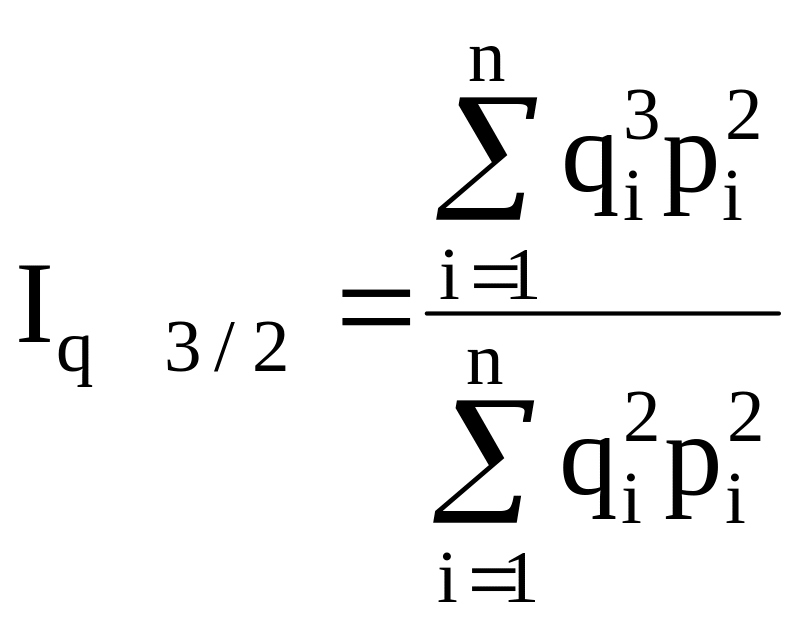и т.д.

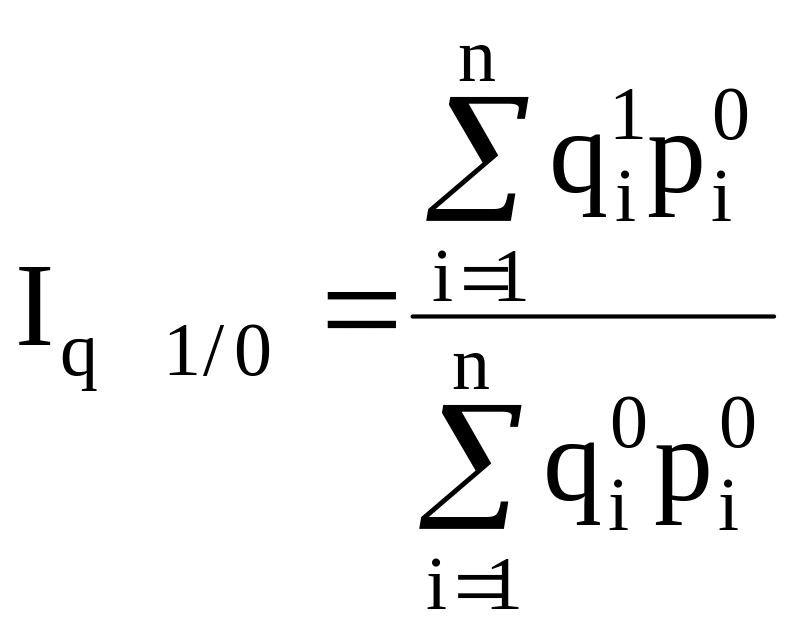
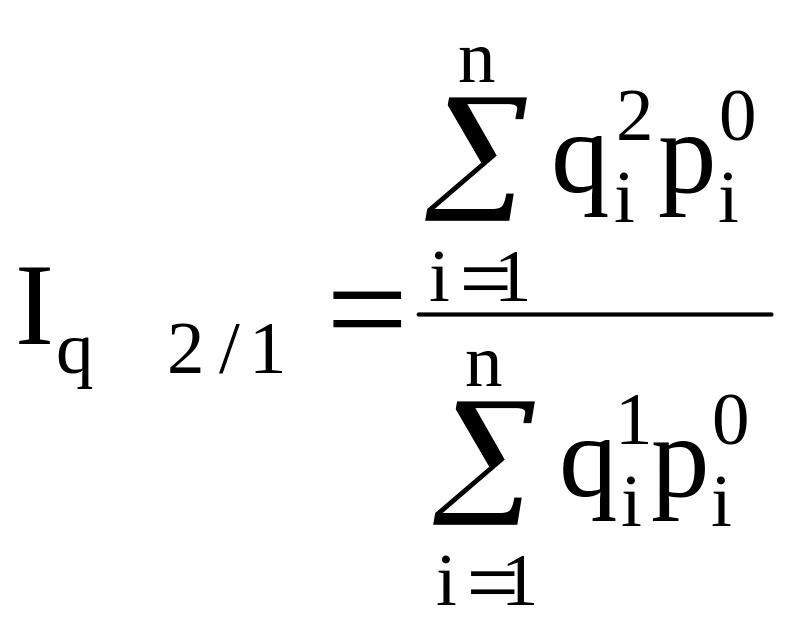
- с постоянными весами: 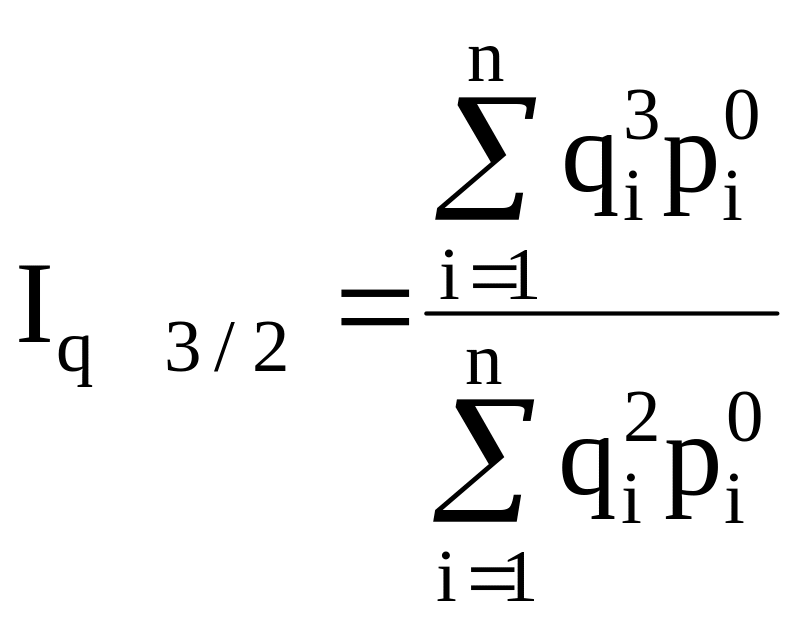и т.д.

Базисные индексы получают при сопоставлении показателя любого периода с показателем одного и того же периода, принятого за базу.

Базисные индексы физического объёма продукции:

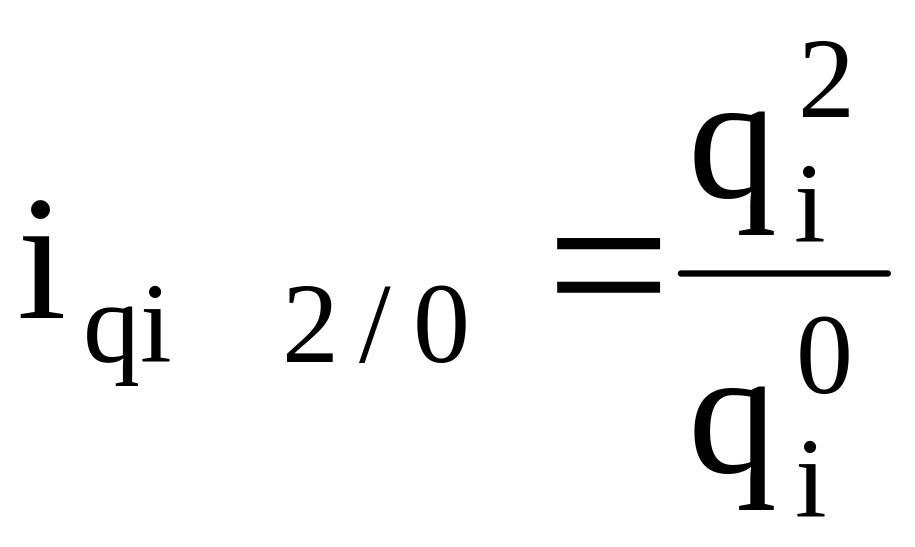
• индивидуальные: 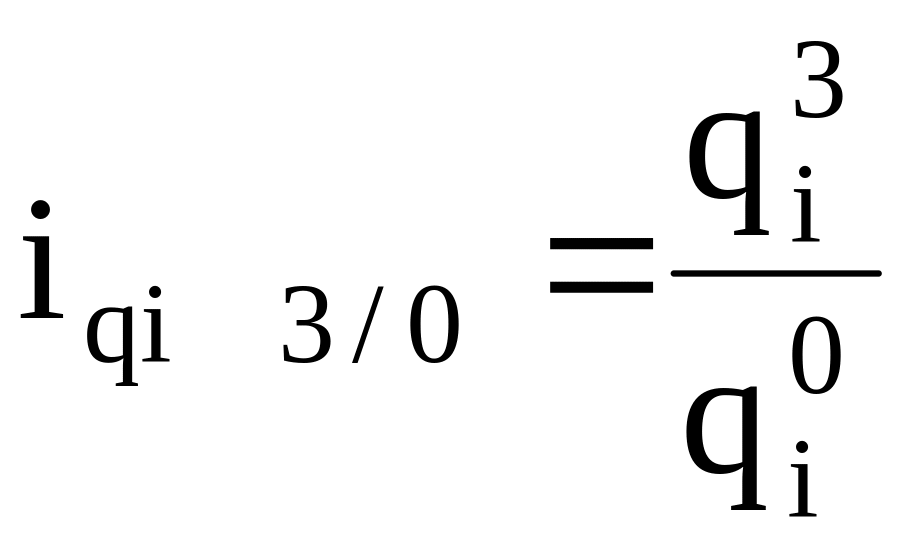и т.д.

• агрегатные

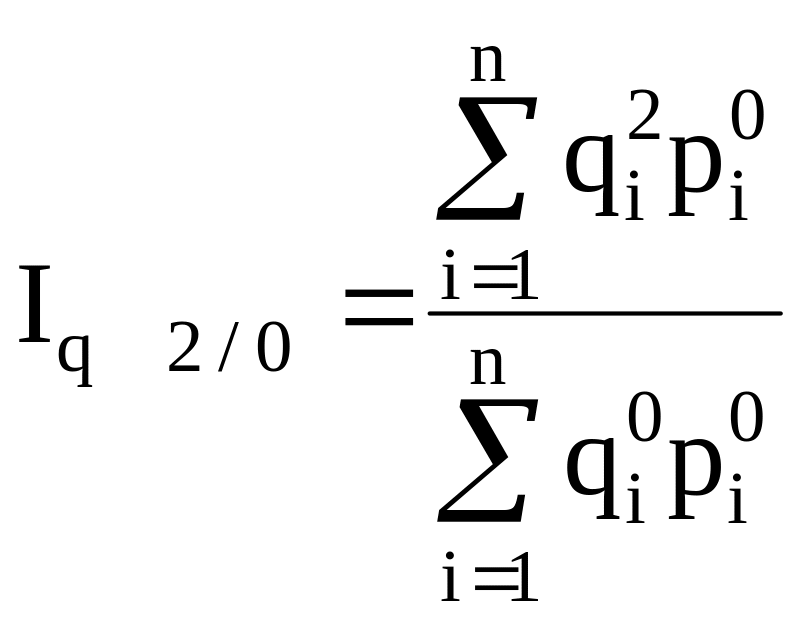
- с постоянными весами 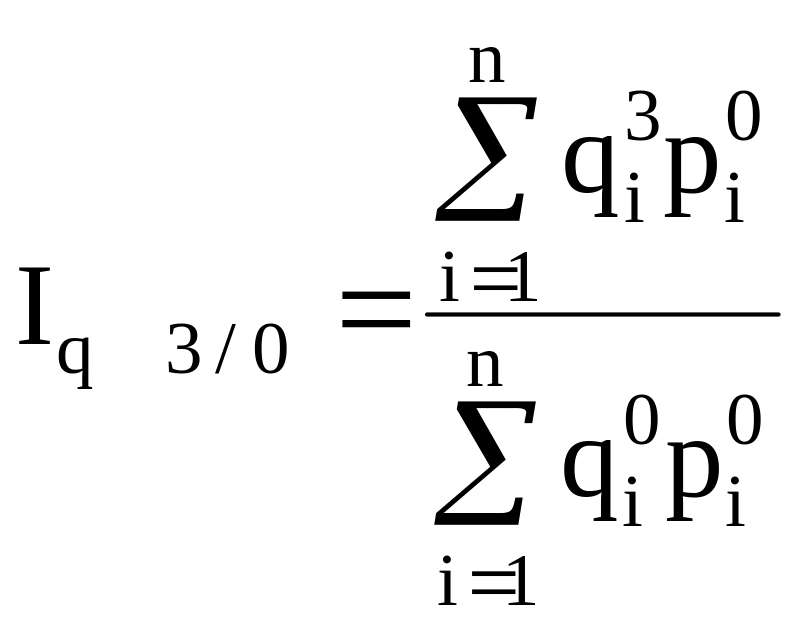и т.д.

- с переменными весами

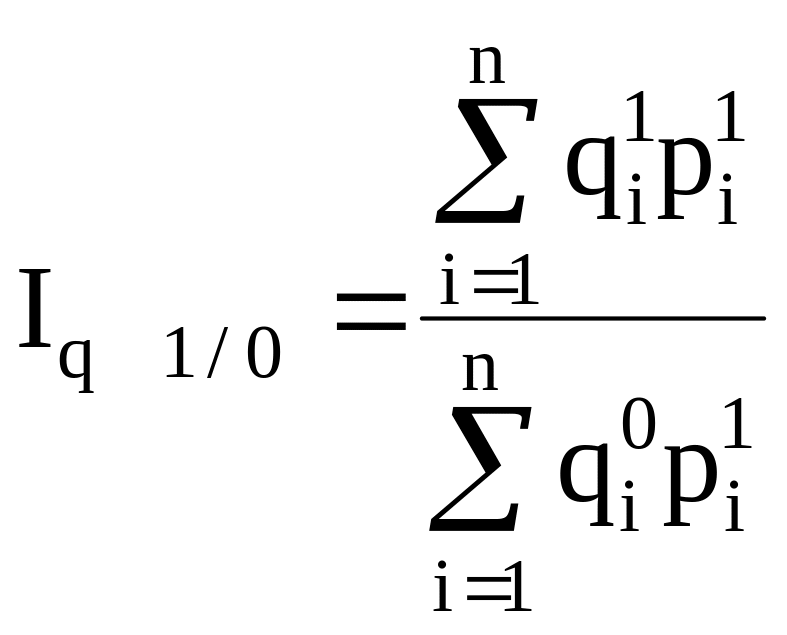
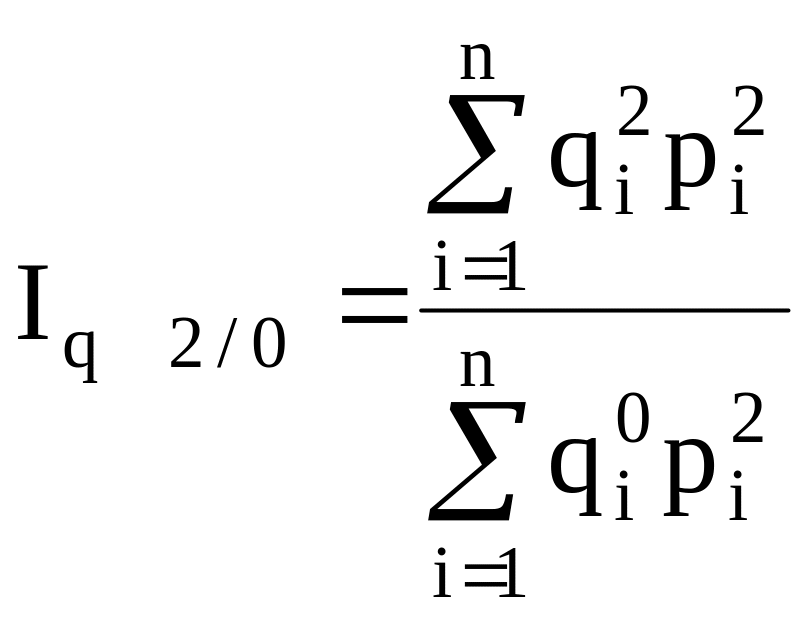
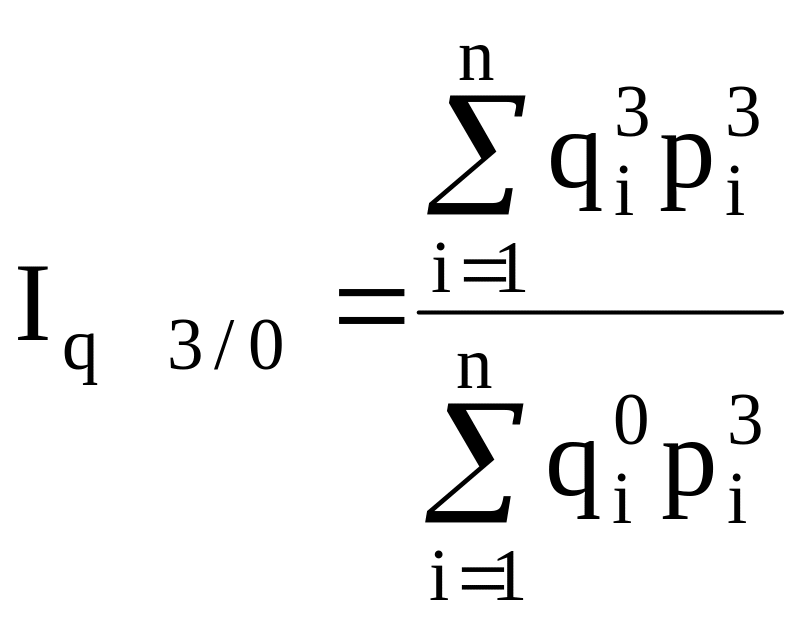
Между цепными и базисными индексами существует взаимосвязь:

Произведение цепных индивидуальных индексов равняется последнему индивидуальных базисному:

; и т.д.

Произведение цепных агрегатных индексов при постоянных весах равняется базисному агрегатному индексу:

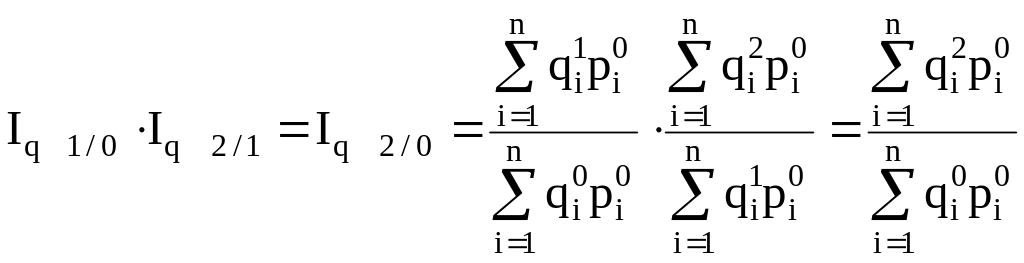и т.д.

Для цен аналогично.

Территориальные индексы

При определении территориальных индексов и сопоставления данных, которые относятся к различным странам и регионам необходимо соблюдать основные требования:

1. характерность весов. Согласно этому требованию для показателей двух стран А и В в качестве весов должны использоваться цены (физический объем товаров) стран А и В (или средние из них), но не цены (физический объем) какой-либо третьей страны С;

2. независимость от выбора базисной страны (требование обратимости индексов во времени, адаптированное к территориальным сопоставлениям). Это требование в математической форме можно записать следующим образом:

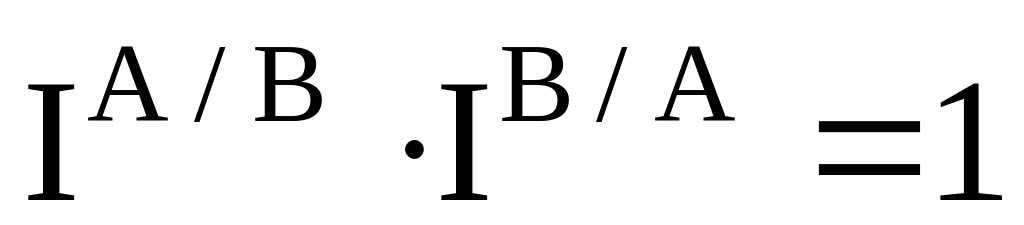
где I^А/В — индекс цен (физического объема) страны А по отношению к стране В;

I^В/А — индекс цен (физического объема) страны В по отношению к стране А;

3. транзитивность. В математической форме это требование можно записать следующим образом:

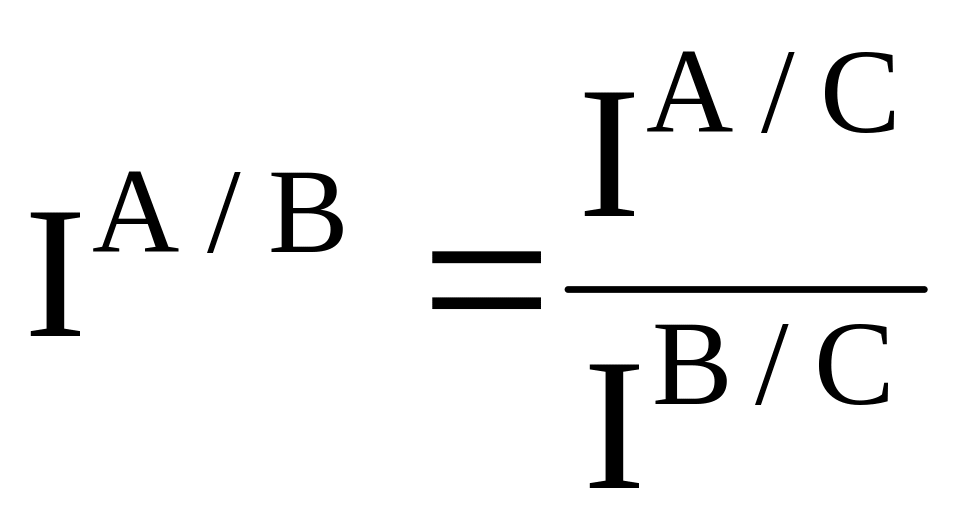
где I^A/C— индекс цен (физического объема) страны А по отношению к стране С;

I^B/C — индекс цен (физического объема) страны В по отношению к стране С.

Суть требования транзитивности состоит в том, что индекс, полученный для некоторой пары стран А и В путем прямого сопоставления их цен (физического объема), должен быть равен этому же индексу, полученному косвенным путем, т.е. делением индекса I^A/C на индекс I^B/C;

4. аддитивность. Согласно требованию аддитивности индексы цен (физического объема), исчисленные для всей совокупности товаров и услуг (например, для ВВП в целом), должны быть четко согласованы с индексами, исчисленными для всех групп этой совокупности. При этом предполагается, что показатели ВВП, исчисленные в ценах базисного периода, должны быть равны сумме компонентов ВВП, также исчисленных в ценах базисного периода;

5. требование факторной пробы. Согласно требованию факторной пробы произведение индекса цен и индекса физического объема должно быть равно индексу стоимости. В математической форме это требование можно записать следующим образом:

- индекс цен показателя (например, ВВП) страны А по отношению к стране В

индекс физического объема показателя (например, ВВП) страны А по отношению к стране В;

индекс стоимости показателя (например, ВВП) страны А по отношению к стране В.

В теории и практике международных сопоставлений различают прямые парные и многосторонние сопоставления.

Прямые парные сопоставления проводятся для какой-либо изолированной пары. На них не влияют показатели третьих стран.

Многосторонние сопоставления проводятся одновременно для группы стран.