3Методи аналізу взаємоз’вязків

3.1Мета заняття

Метою заняття є закріплення теоретичних знань студентів щодо оцінювання щільності зв’язку економічних явищ і побудови регресійних рівнянь факторних ознак.

3.2Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно ознайомитись з літературою [6, c.128-148; 7, с.221-281].

У курсі лекцій [6] надано мінімально необхідні поняття кореляційно-регресійного аналізу, проілюстровано його використання в маркетинговому дослідженні.

У підручнику [7] методологічні основи вивчення кореляційних зв’язків викладені значно глибше, надані методи перевірки значущості коефіцієнтів кореляції, регресії, еластичності, конкордації; докладно розглянуті непараметричні методи перевірки щільності зв’язку.

Для досягнення поставленої мети практичного заняття студент повинен ознайомитися з рекомендованою до вивчення літературою, з теоретичними відомостями даних методичних вказівок, розглянути приклади вирішення задач за темою, а також розв’язати задачі, що запропонував до вирішення викладач.

Перед виконанням практичного завдання студент повинен знати:

1. відмінність кореляційного і функціонального зв’язку;

2. показники щільності зв’язку кількісних, рангових і атрибутивних ознак;

3. види рівняння регресії.

вміти обчислювати:

1. параметри рівняння регресії методом найменших квадратів;

2. коефіцієнти парної кореляції, конкордації, еластичності, -коефіцієнти;

3. коефіцієнти Чупрова, Персона, Спірмена, асоціації, контингенції.

4. визначати значущість моделі і коефіцієнтів регресії;

Стисло наведемо основні теоретичні відомості за темою практичного заняття.

Кореляційно-регресійний аналіз складається із та­ких етапів:

• вибір форми регресії;

• визначення параметрів рівняння;

• оцінка тісноти зв'язку;

• перевірка істотності зв'язку.

При виборі функції використовують графіки, ана­літичні групування, теоретичне обгрунтування. Мож­ливий перебір функцій, коли обчислюють рівняння регресії різних видів і з них вибирають найкраще.

Найбільш поширена у статистичному аналізі ліній­на функція

Y = а + bх.

Параметр b називають коефіцієнтом регресії. Він показує, на скільки одиниць власного виміру в серед­ньому змінюється значення ознаки Y при збільшенні значення ознаки x; на одиницю. Параметр а – це зна­чення Y при х =0.

Якщо х не може приймати нульового значення, то а економічно не інтерпретується і як вільний член рівняння регресії має тільки розрахункове значення.

Ми пропонуємо читачеві, спираючись на свій жит­тєвий досвід, певні реальні значення параметрів для рівняння залежності маси людини від зросту. Іноді суть явища, яке вивчається, приводить до необхідності використання нелінійних рівнянь регресії. При цьому переважно використовують степеневу функцію:

; або гіперболу:

Визначення параметрів рівняння регресії прово­диться методом найменших квадратів, основною умо­вою якого є мінімізація суми квадратів відхилень ем­піричних значень від теоретичних; це дає можливість отримати найкращі оцінки параметрів а і b:

Для їх обчислення складають і розв'язують систему нормальних рівнянь:

Для рішення системи використовують метод де­термінантів:

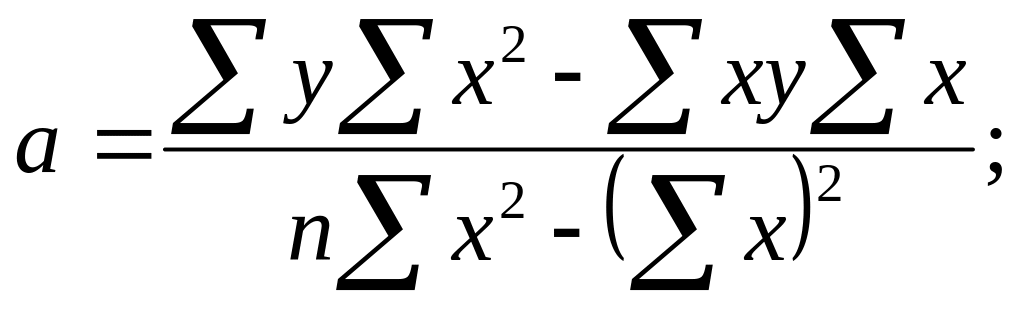
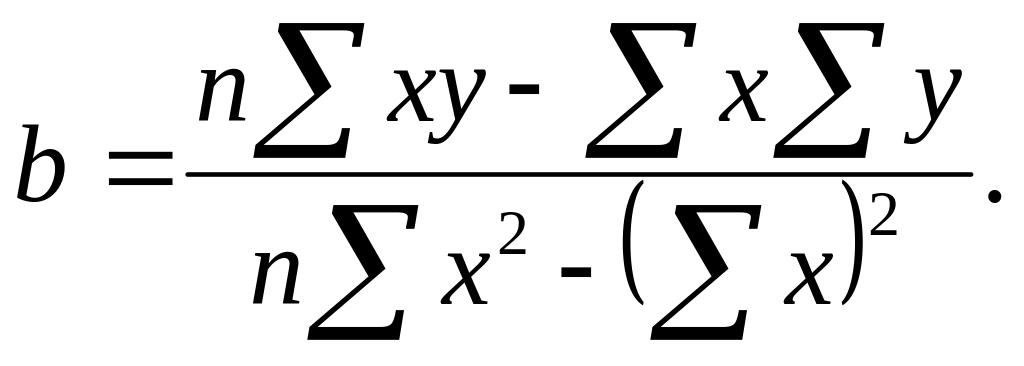
Коли зв'язок між ознаками лінійний, використову­ють лінійний коефіцієнт кореляції, який, приймаючи значення від -1 до +1, характеризує не тільки тісноту зв'язку, а і його напрям. Його абсолютна величина збігається з індексом кореляції.

Його розраховують за наступною формулою:

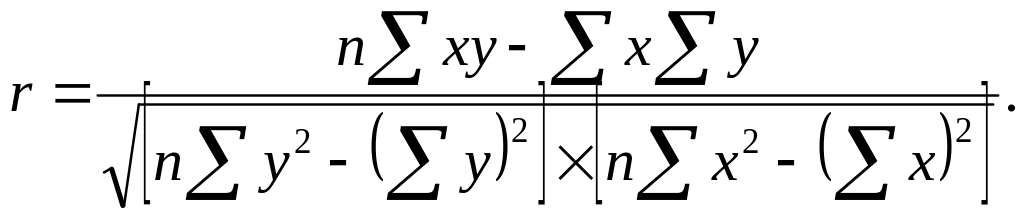
Перевірку істотності зв'язку в КРА здійснюють за допомогою F-критерія Фішера:

де т — число параметрів рівняння регресії.