Міністерство освіти і науки, МОЛОДІ ТА СПОРТУ України

Харківський національний університет радіоелектроніки

МЕТОДИЧНІ ВКАЗІВКИ

до практичних занять з дисципліни «Статистика»

для студентів усіх форм навчання

напряму підготовки 6.030502 «Економічна кібернетика»

галузі знань 0305 «Економіка і підприємництво»

ЗАТВЕРДЖЕНО

Кафедрою економічної кібернетики

Протокол № 10 від 19 травня 2011 р.

Харків 2011

Методичні вказівки до практичних занять з дисципліни «Статистика» для студентів усіх форм навчання спеціальності 6.030502 «Економічна кібернетика»/ Упоряд. Н.В. Ігуменцева - Харків: ХНУРЕ, 2011. - 23 с.

Упорядник Н.В. Ігуменцева.

Рецензент: доцент кафедри статистики, обліку та аудиту НДУ ім. В.Н. Каразіна Чупріна О.А.

Зміст

Вступ 4

1 Ряди розподілу. Показники варіації 5

2 Вибіркове спостереження 11

3 Методи аналізу взаємоз’вязків 15

Перелік посилань 22

Вступ

Об'єктивний аналіз будь-яких масових явищ та процесів потребує наукових методів збору, обробки даних та інтерпретації отриманих результатів. Це стосується соціально-економічних явищ як загального, макроекономічного рівня, так і галузевих, або специфічних. Кількісний аналіз економічних процесів обумовлює викори­стання широкого спектру засобів: від апарату матема­тичної статистики до затверджених відповідними відомствами (Мінстатом та ін.) методик обчислення конкретних показників. Метою дисципліни “Статистика” є оволодіння студентами різними статистичними методами, або мето­дами різних розділів статистики (різних статистичних дисциплін), і перш за все, загальної теорії статистики.

Метою практичних занять є закріплення студентами теоретичних знань, набуття практичних навичок статистичного спостереження, побудови і розрахунку економічних показників, адекватного вибору і кваліфікованого використання статистичних критеріїв перевірки дослідницьких гіпотез.

Навчальний курс орієнтовано на ознайомлення з усіма етапами статистичного дослідження:

1. збирання і реєстрація масових даних про соціально-економічні явища та процеси;

2. забезпечення вірогідності даних;

3. агрегування, зведення і групування інформації;

4. розрахунок узагальнюючих статистичних показників;

5. комплексний порівняльний аналіз;

6. оцінка варіації та концентрації явищ;

7. аналіз структури та структурних зрушень;

8. оцінка щільності та перевірка істотності зв’язків;

9. аналіз динаміки;

10. індексний аналіз.

Зміст курсу побудований таким чином, щоб студент оволодівав статистичними методами в їхній логічній послідовності і системності.

1Ряди розподілу. Показники варіації

1.1Мета заняття

Метою заняття є закріплення теоретичних знань студентів щодо закономірностей статистичного розподілу і його характеристик, зокрема:

1. частотних характеристик;

2. характеристик центру розподілу;

3. характеристик варіації;

4. характеристик нерівномірності розподілу, концентрації, асиметрії, ексцесу.

1.2Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно ознайомитись з літературою [1, c.77-118; 2, с.77-96; 3, с.101-124; 4, с.181-230].

У підручнику [1] викладено основні теоретичні відомості стосовно центру, форми і варіації статистичного розподілу, наведено їхні розрахункові формули та графічне зображення.

У навчальному посібнику [2] нагадується математичне підґрунтя понять варіаційного ряду, точкового та інтервального оцінювання параметрів розподілу ознаки.

Практикум [3] звертає увагу на опис практичних кроків розрахунку показників розподілу статистичних ознак саме економічних об’єктів.

Перед виконанням практичного завдання студент повинен знати:

1. що таке варіація;

2. абсолютні та відносні показники варіації;

3. правило складання дисперсій;

4. види показників центру і форми розподілу;

5. види критеріїв узгодженості;

вміти обчислити:

1. кумулятивні частоти;

2. степеневі середні;

3. моду і медіану (в тому числі графічно);

4. середні лінійне і квадратичне відхилення;

5. коефіцієнти осциляції і варіації;

6. коефіцієнти асиметрії, ексцесу, концентрації;

7. міжгрупову, середню з внутрішньо групових, загальну дисперсії, кореляційне відношення.

Наведемо основні теоретичні відомості з теми практичного заняття.

Ряд розподілу – упорядкована послідовність пар. елементів: варіанта, частота. Варіанта – окреме значення групувальної ознаки; частота – кількість елементів у групі з відповідним значенням (рівнем) ознаки.

Замість частот іноді зручніше вживати частку, виражену коефіцієнтом чи відсотком. Залежно від оз­наки ряди розподілу бувають атрибутивними, як у наведеному вище прикладі, або варіаційними, на­приклад розподіл робітників за рівнем заробітку.

Варіаційні ряди можуть бути дискретними або інтервальними. Дискретні ряди побудовані для перервних, або дискретних ознак. Дискретною є така ознака, яка має певні значення, між якими не може бути ніяких інших (число дітей у сім'ї). Інтервальні ряди будуються, як правило, для неперервних ознак, які можуть приймати будь-які значення в певних межах і виражаються лише приблизно (зріст людини).

Інтервальний ряд може бути побудований і для дискретної ознаки, якщо вона змінюється (варіює) у широких межах (наприклад, розподіл всіх страхових компаній міста за чисельністю працівників). При цьо­му варіанти групуються в інтервали, а частоти відносяться не до окремого значення ознаки, як у дискретних рядах, а до всього інтервалу.

Середня в статистиці абстрактна узагальнююча величина, що характеризує рівень варіюючої ознаки в якісно однорідній сукупності. Коливання індивідуальних значень ознаки, викликані дією різних факторів, урівноважуються в середній величині.

Середні, що застосовують у статистиці, належать до класу степеневих, які в узагальненій формі мають ви­гляд:

,

де х — індивідуальні значення варіюючої ознаки (варіанти); z — показник степеня середньої; п — число варіант.

Мода (Мо) — значення варіанти, яке найчастіше повторюється в ряді розподілу. У дискретному ряді моду легко відшукати візуально, у інтервальному ряді легко відшукати модальний інтервал, а приблизне значення моди обчислюється за формулою

,

де х_Мо – нижня межа модального інтервалу; і_Мо – роз­мір модального інтервалу; f_Мо – частота модального інтервалу; f_Мо-1 – частота попереднього інтервалу; f_Мо+1 – частота інтервалу, наступного за модальним.

Медіана (Ме) – варіанта, що ділить ранжирований ряд на дві, рівні за чисельністю, частини. Так, якщо в ряді розподілу робітників за віком Ме = 34, то це означає, що половина з них менші цього віку, половина – старші цього віку. Коли ряд містить парне число членів, медіана дорівнює середній із двох зна­чень розташованих всередині ряду. Для знаходження медіани в дискретному ряді спочатку обчислюють півсуму частот, а потім визначають, яка варіанта при­падає на неї. Для інтервального ряду медіану обчис­люють за формулою

,

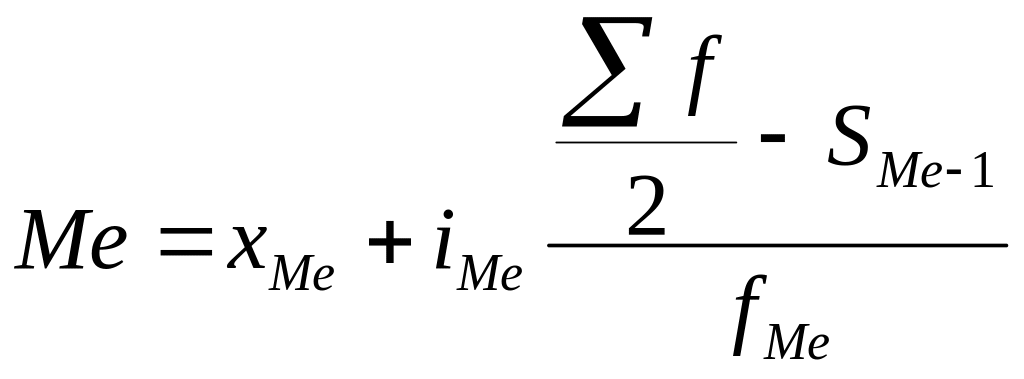де х_Ме – нижня межа медіанного інтервалу; і_Ме – розмір медіанного інтервалу; – півсума частот; – сума накопичених частот перед медіанним інтервалом; f_Ме — частота ме­діанного інтервалу.

Середнє відхилення обчислюється як:

1) середнє лінійне відхилення:

а) незважене: б) зважене:

, ;

2) середнє квадратичне відхилення:

а) незважене: б) зважене:

, .

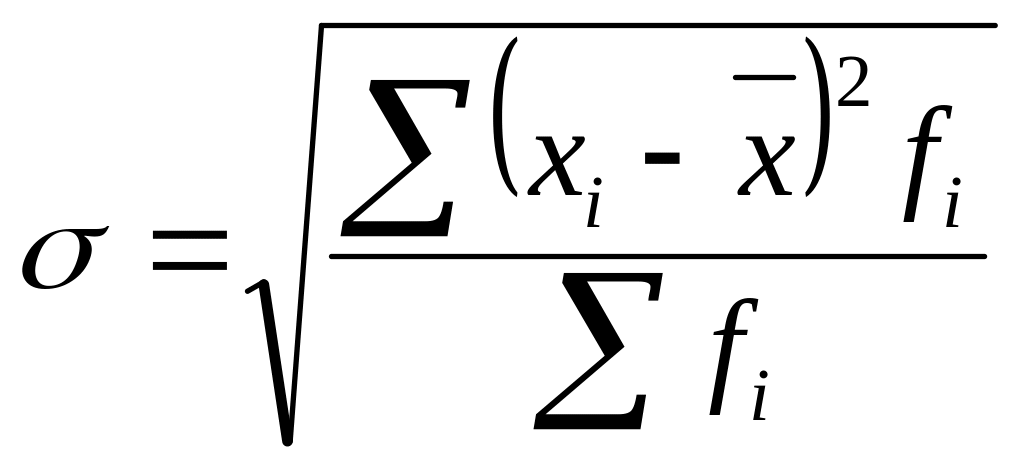Характеристика варіації має назву дисперсії:

а) незважена: б) зважена:

, .

При порівнюванні степеня варіації однієї і тієї ж ознаки в різних сукупностях використовують коефіцієнт варіації:

.

Характеристики форми розподілу грунтуються на моментах розподілу. Момент розподілу — це се­редня k-го ступеня відхилень x – а.

Залежно від величини а моменти поділяються на первинні (а = 0), центральні (а = x) і умовні (а = const). Ступінь k визначає порядок моменту [2]. В літературі звичайно записують

.

Тоді , а ,

де ; .