
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Дана функция распределения непрерывной случайной величины
- •Вариант 6
- •Вариант 7
- •Дана функция распределения непрерывной случайной величины
- •Вариант 8
- •Дана функция распределения непрерывной случайной величины .
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Дана плотность распределения случайной величины
- •Вариант 12
- •Вариант 13
- •Дана плотность распределения случайной величины
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Задана функция распределения непрерывной случайной величины .
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Рабочий берет две детали. События: – хотя бы одна из них бракованная, – обе бракованные. Что означают события
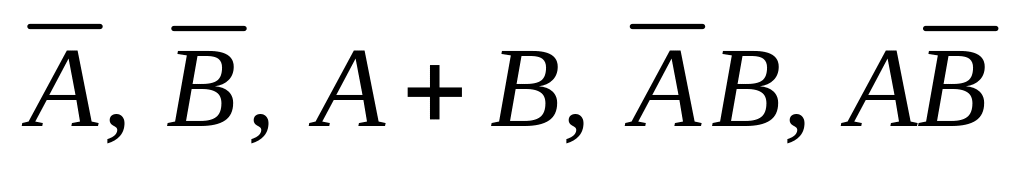 ?
?В записанном телефонном номере две последние цифры стерлись. Определить вероятность того, что это а) различные цифры, б) одинаковые цифры.
Значения и равно–возможны в квадрате
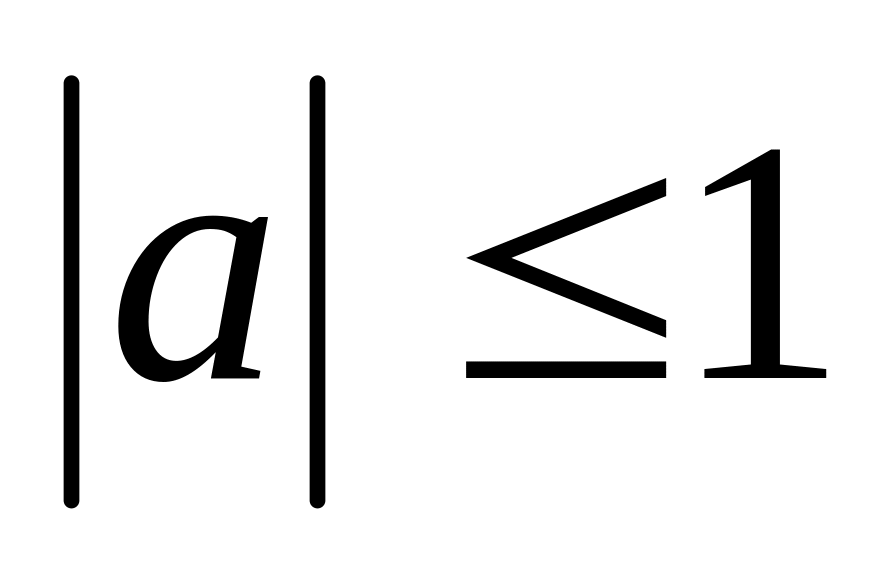 ,
,
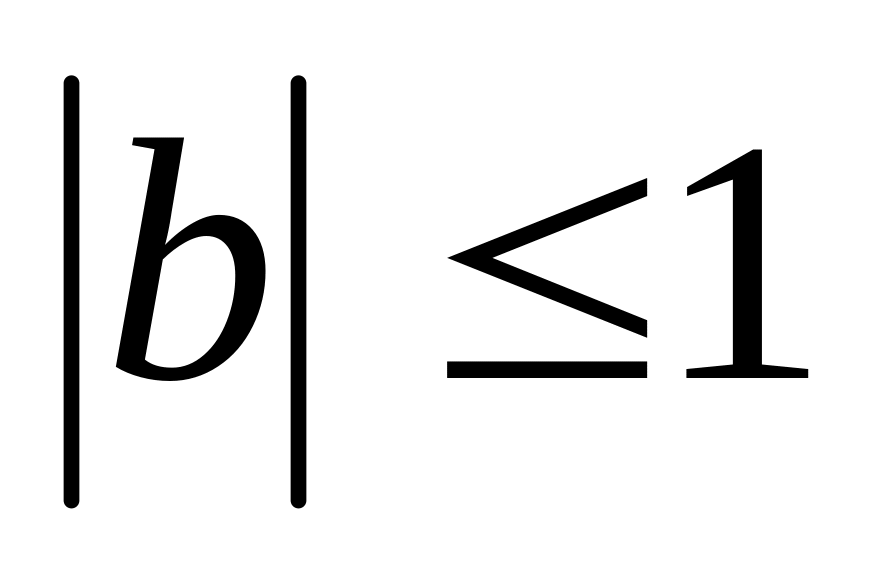 .
Найти вероятность того, что корни
квадратного трехчлена
.
Найти вероятность того, что корни
квадратного трехчлена
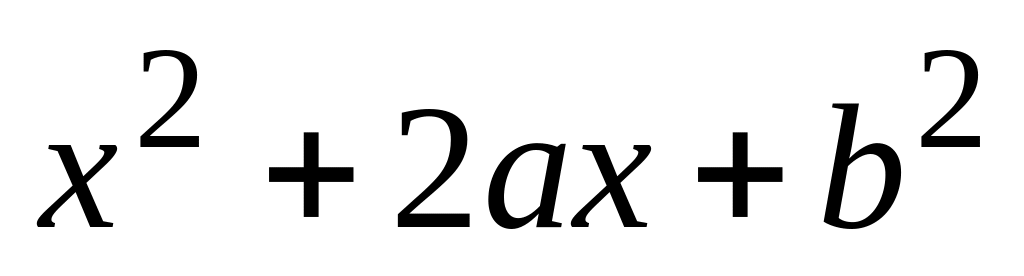 положительны.
положительны.Транзисторный приемник смонтирован на полупроводниках, для которых вероятность брака равна . Найти вероятность того, что радиоприемник будет неработоспособным, если он отказывает при наличии в нем не менее одного бракованного полупроводника.
Количество испорченных лампочек на штук равновозможно от до . а) Определить вероятность того, что две лампочки, взятые наудачу из , окажутся исправными; б) Две лампочки, взятые наудачу из , оказались исправными. Найти вероятность того, что при этом среди лампочек было бракованных.
В урне черных и белых шаров. Шар извлекается из урны, а затем возвращается назад. Определить вероятность того, что при пяти извлечениях будет белых шара.
Случайная величина – число белых шаров в предыдущей задаче. Найти 1) ряд распределения, 2) функцию распределения и ее график; 3) ; 4) ; 5) СКВО, моду и медиану; 5) СКВО; 6)
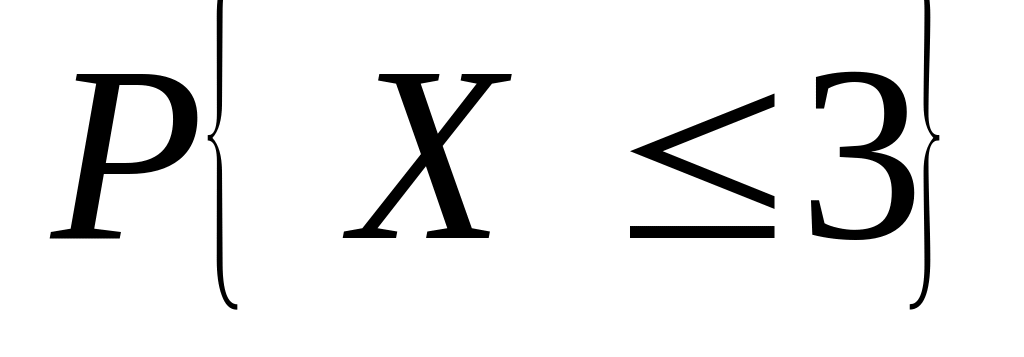 .
.Дана плотность распределения случайной величины
![]()
Найти:
,
,
,
СКВО, моду и медиану, функцию распределения
,
![]() .
.
Устройство состоит из
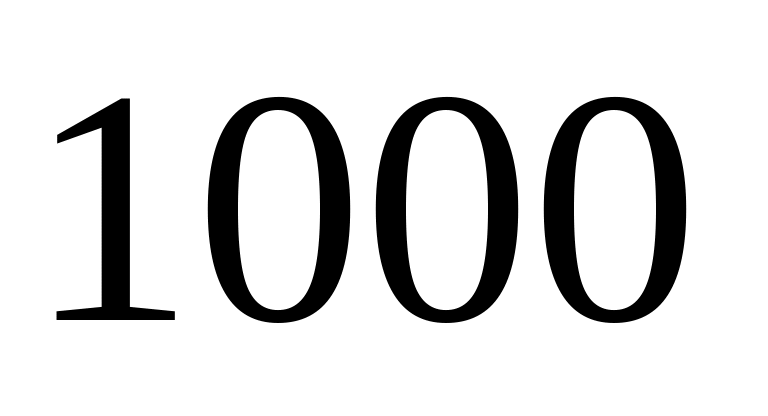 элементов, работающих независимо один
от другого. Вероятность отказа любого
элемента в течение часа равна
элементов, работающих независимо один
от другого. Вероятность отказа любого
элемента в течение часа равна
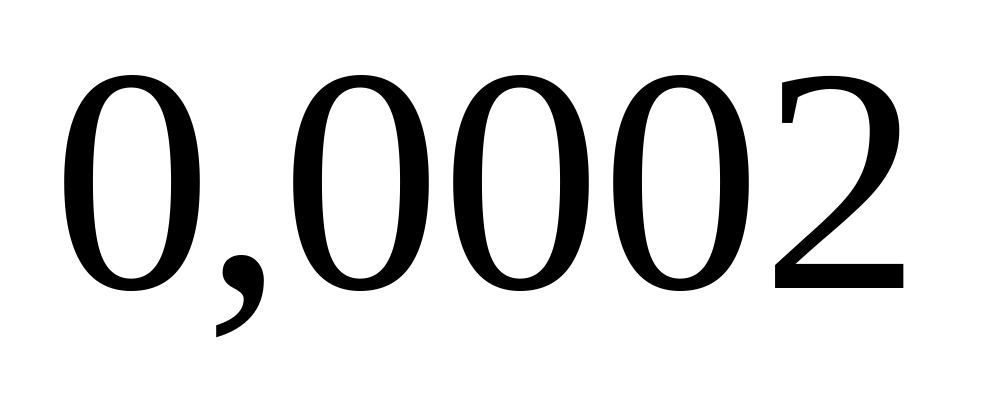 .
Найти вероятность, что в течение
.
Найти вероятность, что в течение
 часов откажут ровно четыре элемента.
часов откажут ровно четыре элемента.Изделие считается высшим сортом, если его вес не превосходит по абсолютной величине г. Ошибка взвешивания подчинена нормальному закону с параметрами
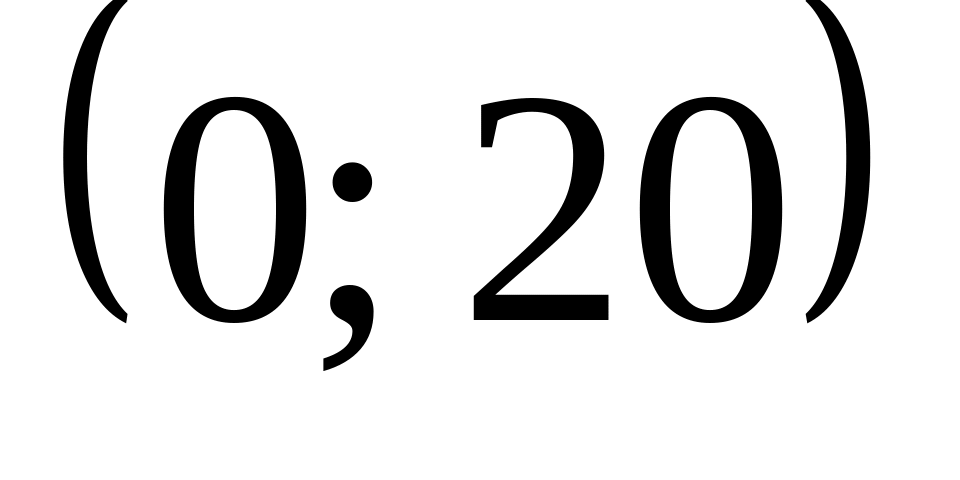 .
Найти среднее число изделий высшего
сорта, если изготовлено три изделия.
Взвешивание деталей производится
независимо.
.
Найти среднее число изделий высшего
сорта, если изготовлено три изделия.
Взвешивание деталей производится
независимо.
Вариант 14
Рабочий изготовил две детали. Событие
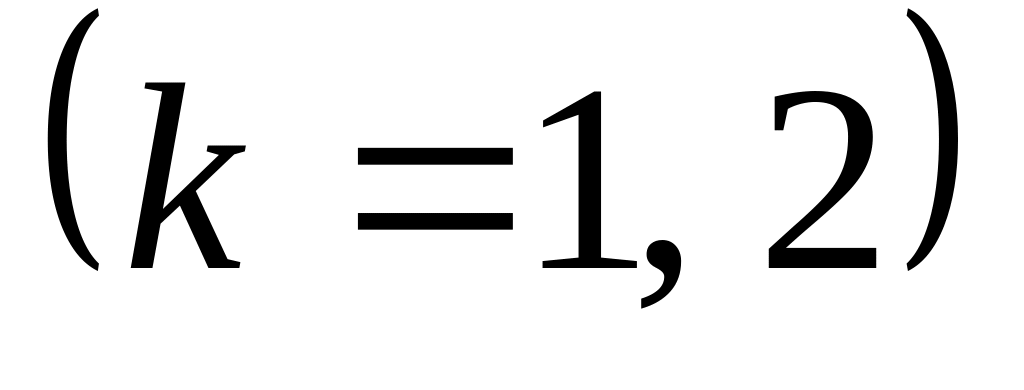 –
-я
деталь имеет дефект. Записать через
события:
– ни одна из деталей не имеет дефекта,
– хотя бы одна деталь имеет дефект,
– обе детали дефектны.
–
-я
деталь имеет дефект. Записать через
события:
– ни одна из деталей не имеет дефекта,
– хотя бы одна деталь имеет дефект,
– обе детали дефектны.В кошельке лежат три монеты достоинством рубль и семь монет по
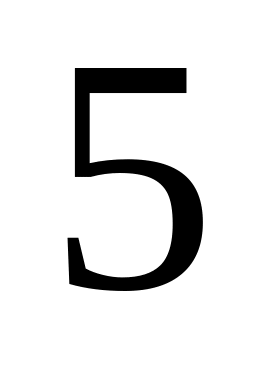 рублей. Наудачу берутся две монеты.
Определить вероятность того что: а) обе
монеты по
рублю; б) одна достоинством
рубль, другая –
рублей.
рублей. Наудачу берутся две монеты.
Определить вероятность того что: а) обе
монеты по
рублю; б) одна достоинством
рубль, другая –
рублей.Наудачу взяты два положительных числа не больше единицы. Определить вероятность того, что их сумма не меньше
 .
.Вероятность того, что цель поражена при одном выстреле первым стрелком, равна , вторым – . Первый сделал два выстрела, второй один. Определить вероятность того, что цель поражена.
В течение рабочего дня два сотрудника кредитного банка выполняют
 %
и
%
и
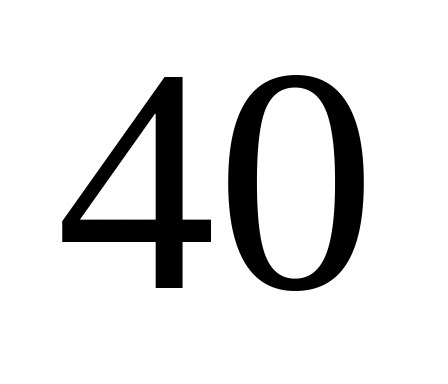 %
от общего объема работы, а стажер всего
%
от общего объема работы, а стажер всего
 %.
Вероятность совершить ошибку при
заключении договора для них равны
%.
Вероятность совершить ошибку при
заключении договора для них равны
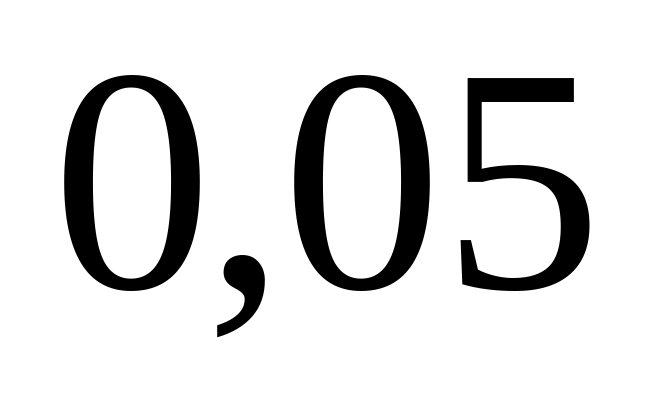 ;
и
;
и
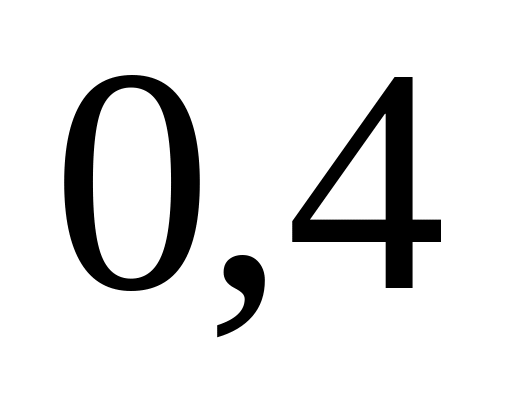 соответственно. Найти вероятность
того, что а) один из договоров пришлось
исправлять; б) ошибку сделал стажер,
если известно, что один из договоров
пришлось исправлять.
соответственно. Найти вероятность
того, что а) один из договоров пришлось
исправлять; б) ошибку сделал стажер,
если известно, что один из договоров
пришлось исправлять.Устройство состоит из четырех независимо работающих элементов. Вероятности отказа каждого из элементов за время Т одинаковы и равны . Найти вероятность отказа прибора за время Т, если для этого достаточно, чтобы отказали хотя бы три элемента из четырех.
Случайная величина – число отказов устройства в предыдущей задаче. Найти: 1) ряд распределения, 2) функцию распределения и ее график; 3) ; 4) ; 5) СКВО, моду и медиану; 6)
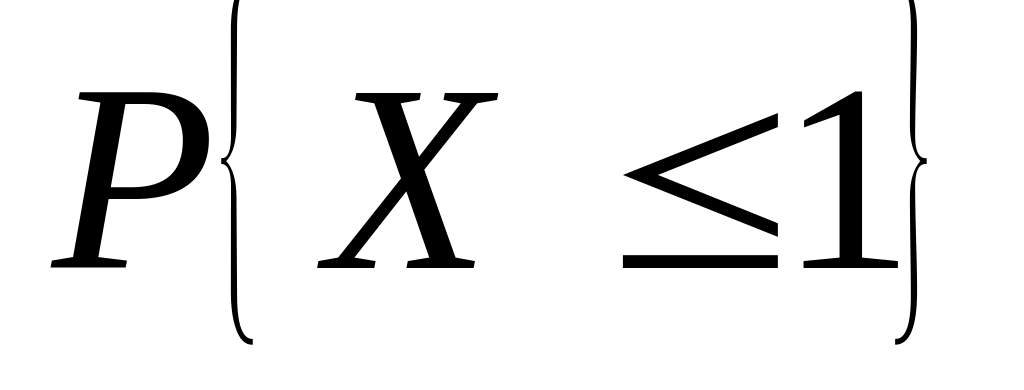 .
.Задана функция распределения случайной величины
![]() .
.
Найти:
,
,
,
,
СКВО, моду и медиану; плотность
распределения
,
![]() .
.
Приемник состоит из независимо работающих элементов. Вероятность безотказной работы его в течение года равна
 .
Найти вероятность
.
Найти вероятность
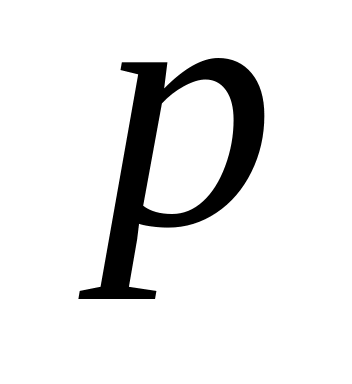 выхода из строя одного элемента в
течение месяца, если эта вероятность
одинакова для всех элементов.
выхода из строя одного элемента в
течение месяца, если эта вероятность
одинакова для всех элементов.Случайная ошибка измерений подчинена нормальному закону с параметрами
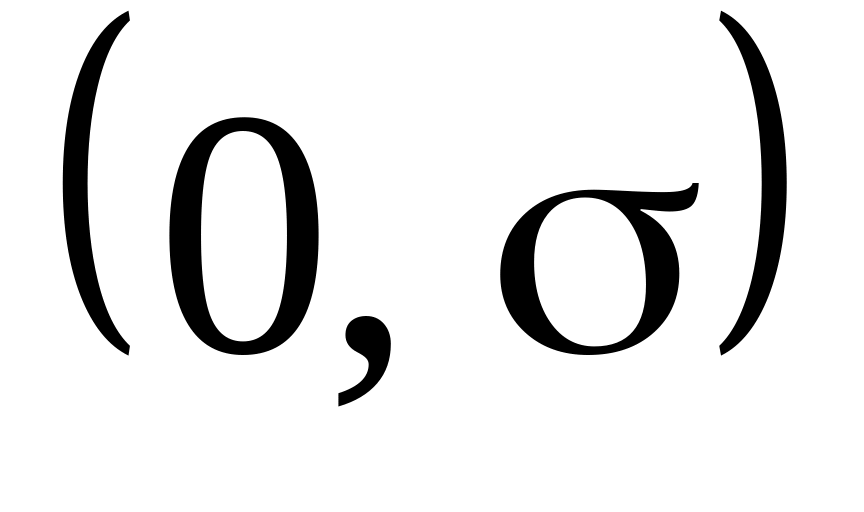 .
Найти
.
Найти
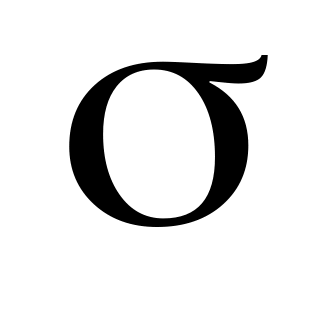 ,
при котором вероятность попадания
обшивки в интервал
,
при котором вероятность попадания
обшивки в интервал
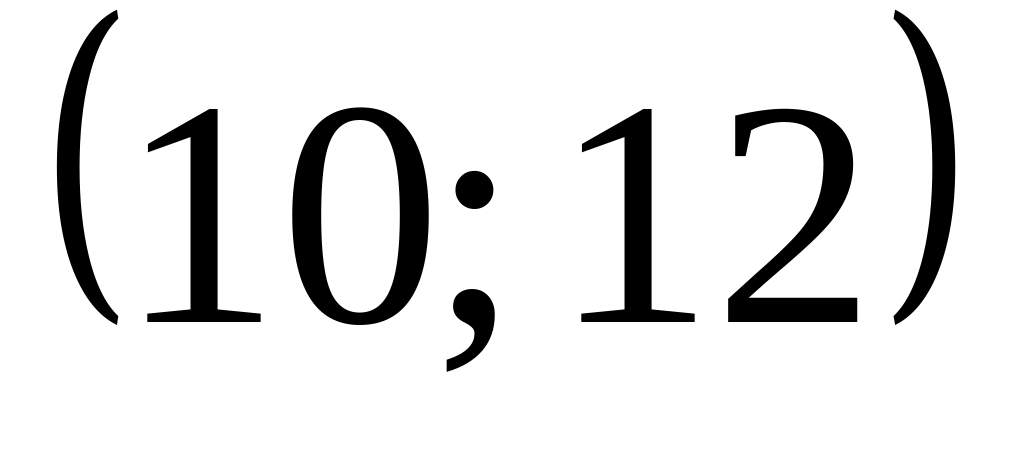 будет равна
будет равна
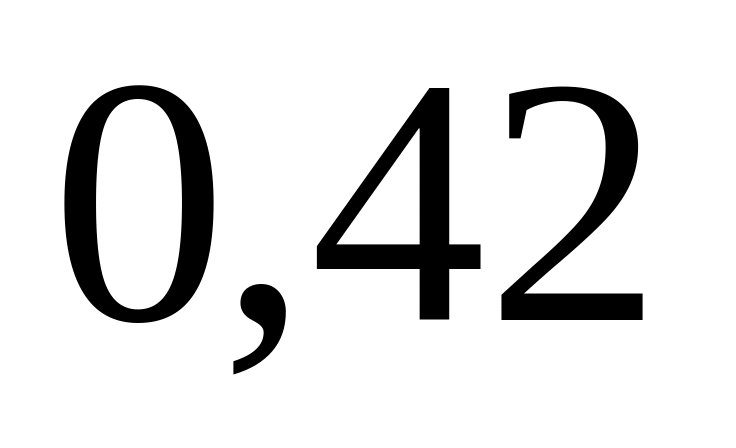 .
.
Вариант 15
Рабочий обслуживает три автоматических станка. События: - первый станок потребует внимания в течение часа, – второй потребует внимания в течение часа, – третий потребует внимания в течение часа. Что означают события:
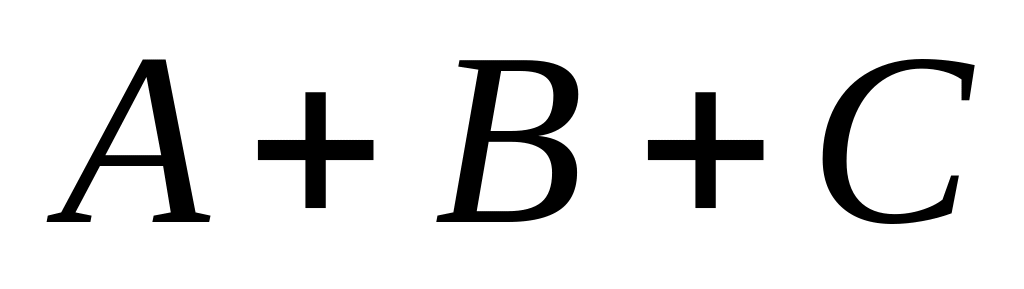 ,
,
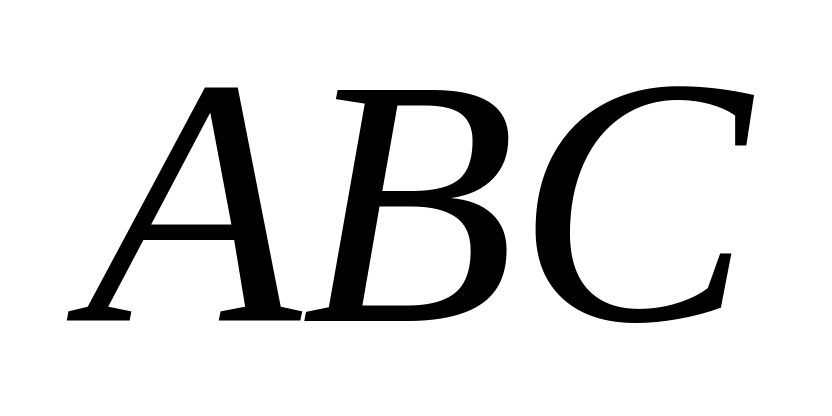 ,
,
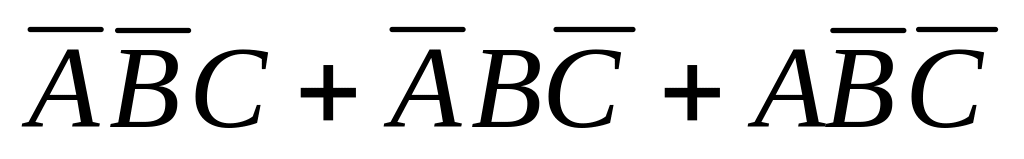 ?
?Найти вероятность того, что дни рождения трех подруг придутся на разные месяцы года, если попадание на любой месяц года равно-возможно.
На отрезке
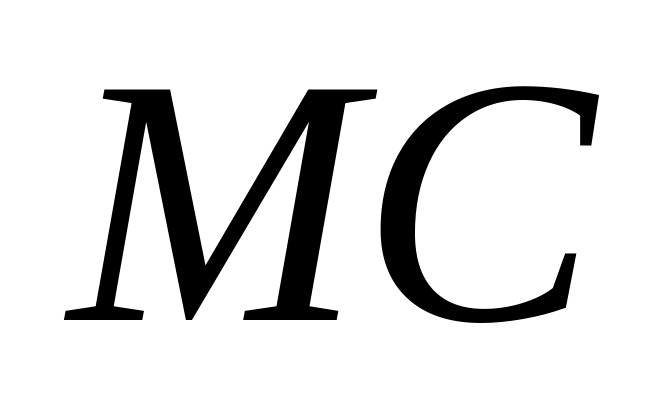 длиной
см наудачу поставлены две точки
и
.
Найти вероятность того, что точка
будет ближе к точке
,
чем к точке
длиной
см наудачу поставлены две точки
и
.
Найти вероятность того, что точка
будет ближе к точке
,
чем к точке
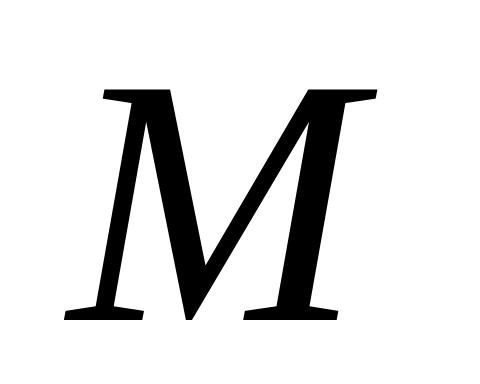 .
.В ящике деталей, из которых деталей окрашены. Сборщик наудачу взял три детали. Какова вероятность, что хотя бы одна окрашена.
Станок одну треть своего времени обрабатывает деталь , а две трети – деталь . При обработке детали он простаивает % времени, а детали – % времени. Какова вероятность того, что а) станок оказался простаивающим; б) простой станка произошел при обработке детали .
Две монеты бросают пять раз. Определить вероятность того, что два герба появятся только один раз.
Случайная величина – число выпадений «двойных гербов» в предыдущей задаче. Найти: 1) ряд распределения, 2) функцию распределения и ее график; 3) ; 4) ; 5) СКВО, моду и медиану; 6)
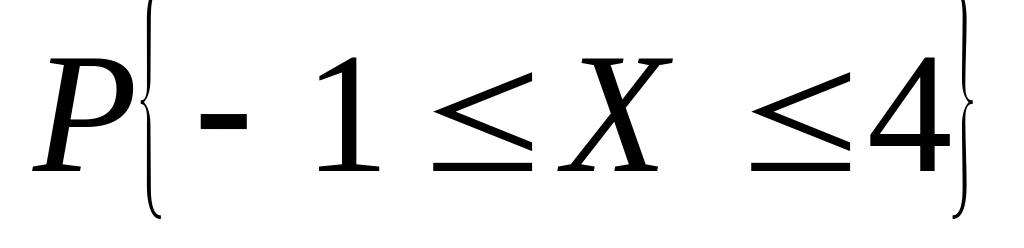 .
.Задана плотность распределения случайной величины
![]() .
.
Найти:
,
,
,
СКВО, моду и медиану; функцию распределения
;
![]() .
.
Устройство состоит из независимо работающих элементов. Вероятность выхода из строя любого элемента в течение рабочего дня равна
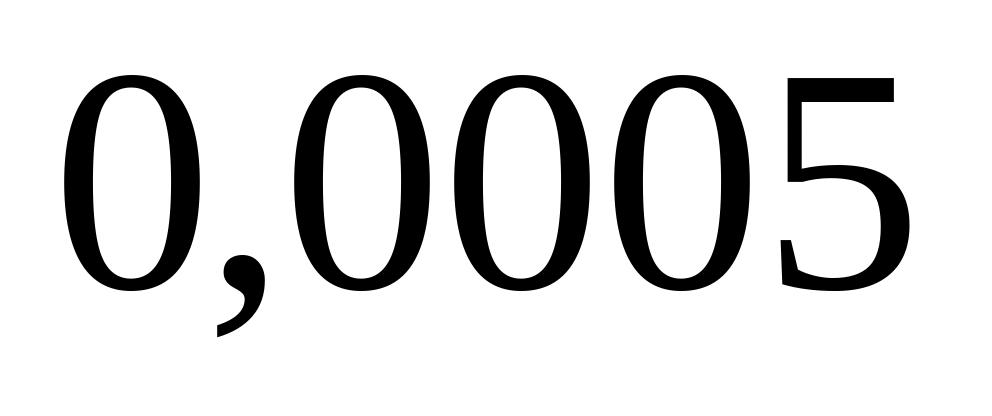 .
Найти вероятность безотказной работы
устройства в течение одной пятидневной
недели.
.
Найти вероятность безотказной работы
устройства в течение одной пятидневной
недели.
Случайная ошибка измерений подчинена нормальному закону с параметрами
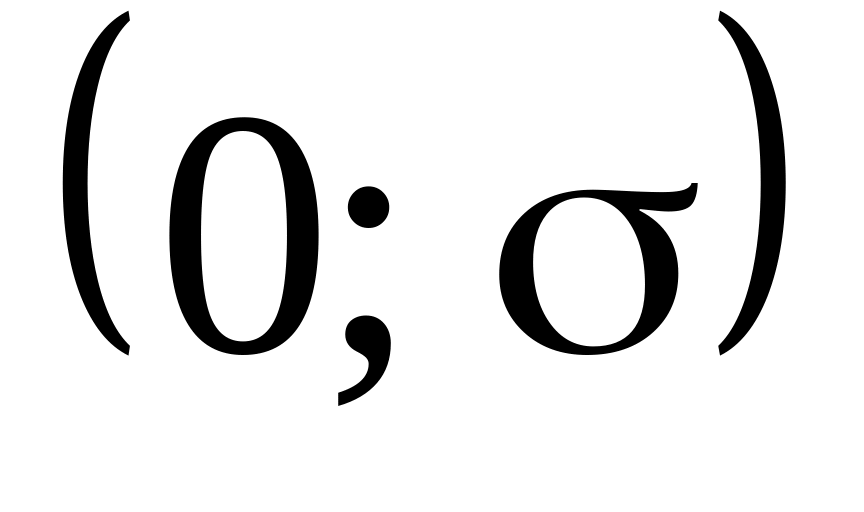 .
Найти
,
если вероятность того, что ошибка
измерения не превосходит по абсолютной
величине
мм,
равна
.
.
Найти
,
если вероятность того, что ошибка
измерения не превосходит по абсолютной
величине
мм,
равна
.
