
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Дана функция распределения непрерывной случайной величины
- •Вариант 6
- •Вариант 7
- •Дана функция распределения непрерывной случайной величины
- •Вариант 8
- •Дана функция распределения непрерывной случайной величины .
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Дана плотность распределения случайной величины
- •Вариант 12
- •Вариант 13
- •Дана плотность распределения случайной величины
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Задана функция распределения непрерывной случайной величины .
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Прибор состоит из двух блоков первого и трех блоков второго типа. События:
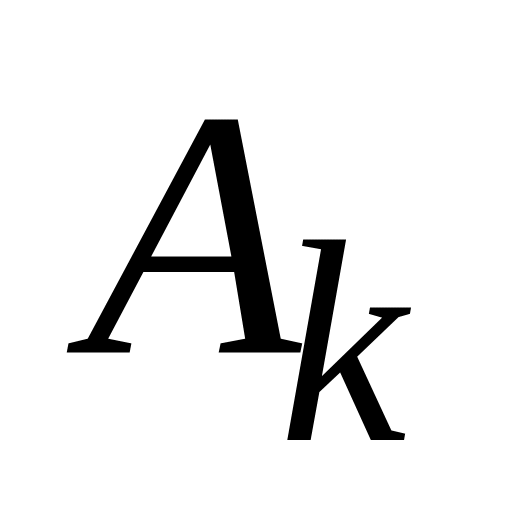 ,
,
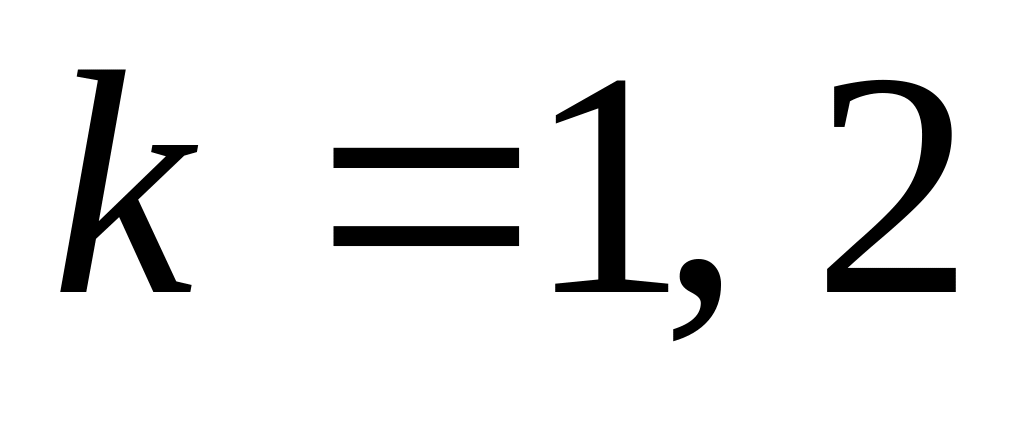 – исправен
– исправен
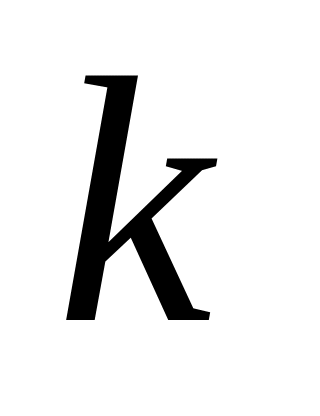 - й
блок первого типа;
- й
блок первого типа;
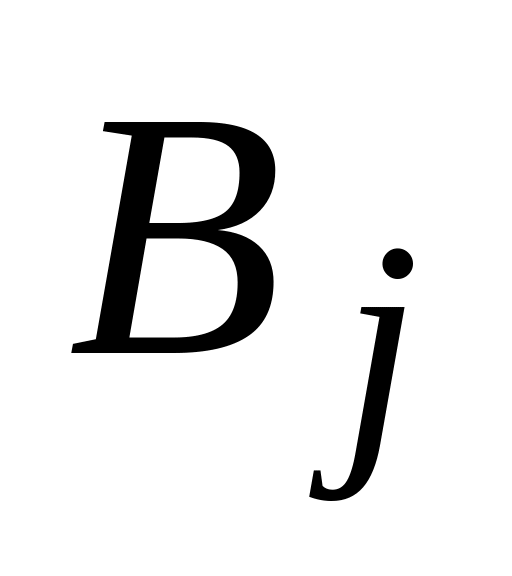 ,
,
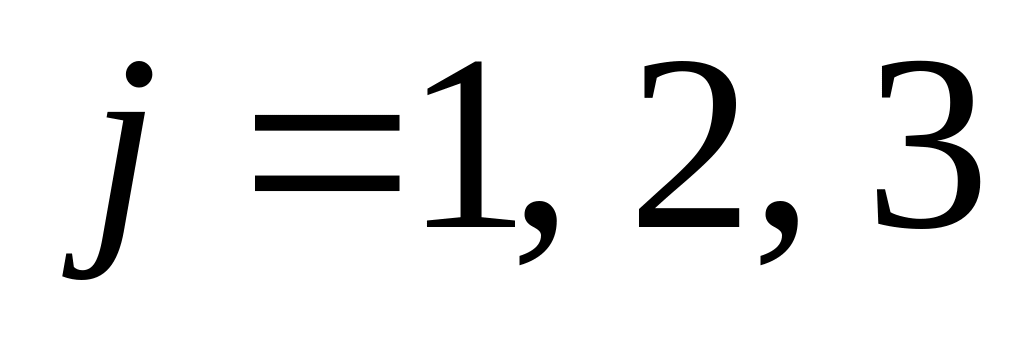 – исправен
– исправен
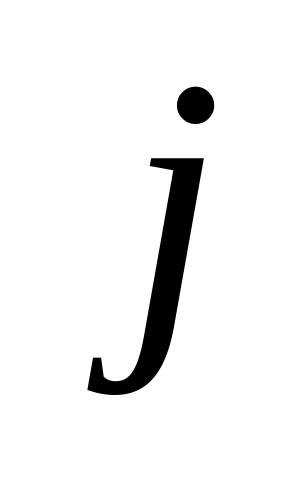 - й
блок второго типа,
– прибор исправен. Событие
появляется, если исправны оба блока
первого типа и хотя бы один второго.
Выразить
через
и
.
- й
блок второго типа,
– прибор исправен. Событие
появляется, если исправны оба блока
первого типа и хотя бы один второго.
Выразить
через
и
.Имеется множество
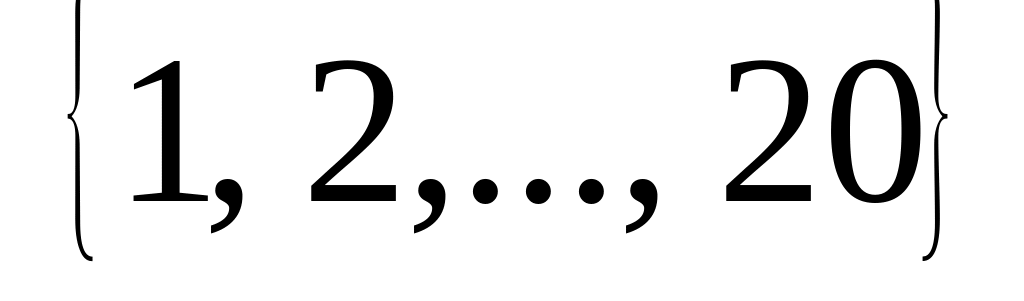 .
Из него извлечено два числа. Определить
вероятность того, что а) оба числа
четные; б) одно четное, другое нечетное.
.
Из него извлечено два числа. Определить
вероятность того, что а) оба числа
четные; б) одно четное, другое нечетное.На отрезке длиной
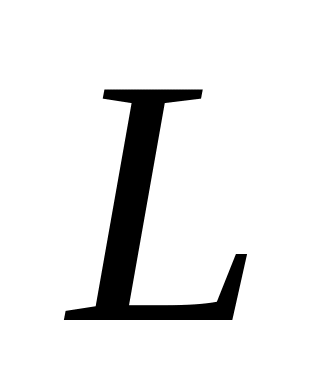 наудачу выбраны две точки. Какова
вероятность, что расстояние между ними
меньше половины
?
наудачу выбраны две точки. Какова
вероятность, что расстояние между ними
меньше половины
?В урне один белый и два черных шара. Два игрока поочередно извлекают шары. Выигрывает тот, кто первый вынет белый шар. Определить вероятность выигрыша начинающего игру.
В тире имеется пять ружей, вероятности попаданий из которых равны соответственно , , , , . Стреляющий берет одно из ружей наудачу и делает выстрел. а) Определить вероятность того, что сделанный выстрел попал в цель. б) Сделанный выстрел попал в цель. Какова вероятность того, что до этого было взято первое ружье.
Две кости одновременно бросают три раза. Определить вероятность того, что "двойная шестерка" выпадет точно один раз.
Случайная величина – выпадение "двойной шестерки" в предыдущей задаче. Найти 1) , 2) функцию распределения и ее график; 3) ; 4) ; 5) СКВО, моду и медиану; 6)
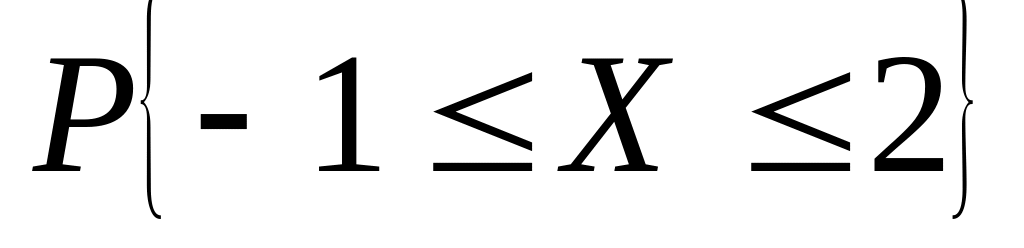 .
.Дана плотность распределения случайной величины
![]()
Найти:
,
,
,
СКВО, моду и медиану, функцию распределения
,
![]() .
.
На заводе станков, каждый из которых выходит из строя в течение часа с вероятностью . Какова вероятность, что за смену ( часов) выйдет из строя ровно станков?
Автомат изготовляет шарики. Шарик годный, если отклонение диаметра шарика от нормы по абсолютной величине меньше мм. Случайная величина распределена нормально с параметрами . Найти вероятность того, что из независимо проверенных шариков хотя бы один годный.
Вариант 12
Из таблицы случайных чисел взято наудачу число. События:
 – число четное,
– число четное,
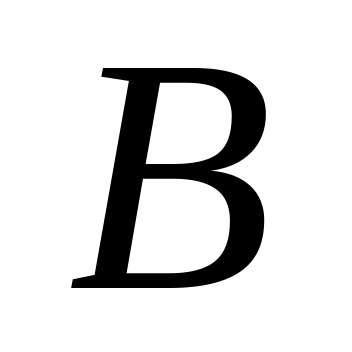 – число оканчивается на ноль. Что
означают события
– число оканчивается на ноль. Что
означают события
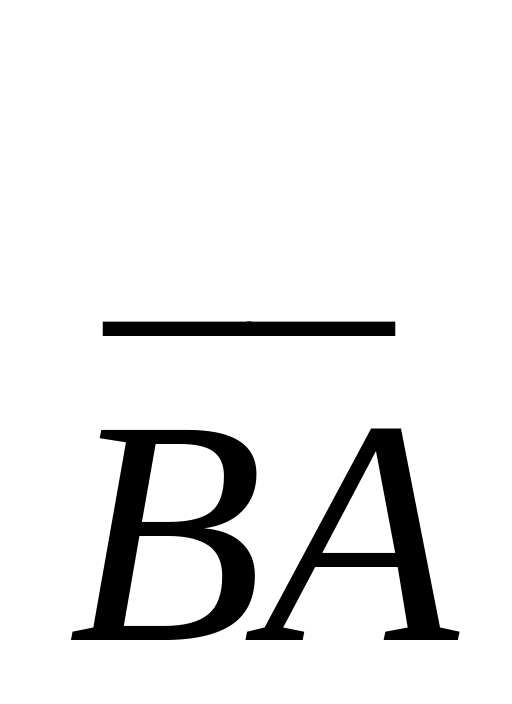 ,
,
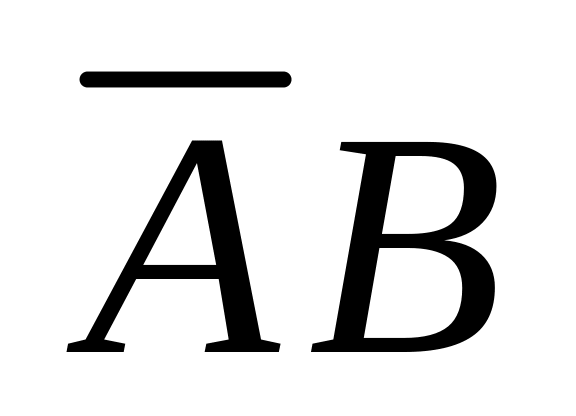 ,
,
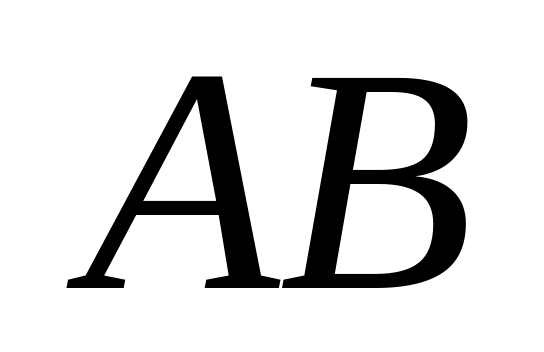 ,
,
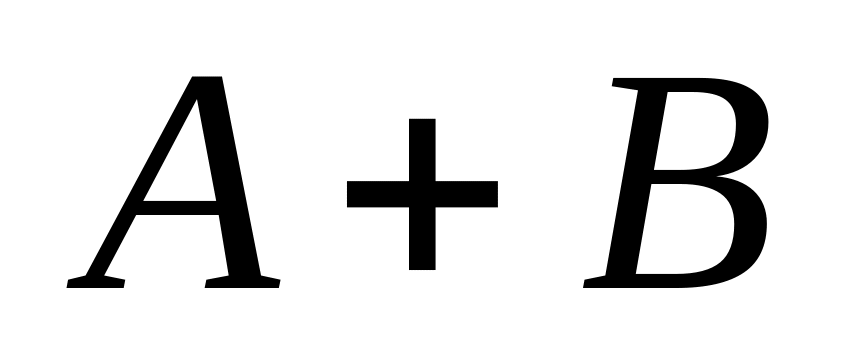 ,
,
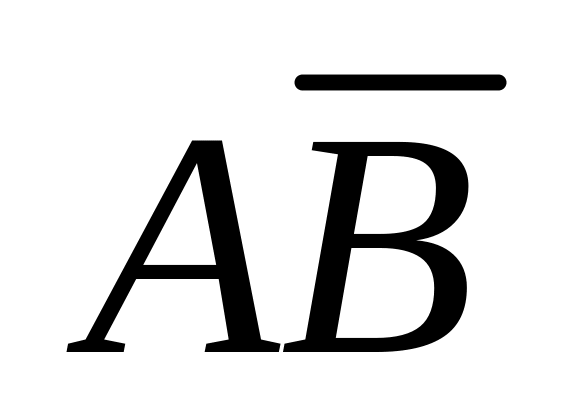 ?
?В конверте среди карточек находится нужная карточка. Наудачу взяты шесть карточек. Какова вероятность, что среди них нужная?
На отрезке единичной длины наудачу появляется точка. Определить вероятность того, что расстояние от точки до концов отрезка превосходит .
На полке расставлено учебников, из них в переплете. Взяли учебника. Какова вероятность, что хотя бы один будет в переплете.
Из трех партий взята для испытания одна деталь. Она с равной вероятностью может быть взята из каждой партии. В первой партии
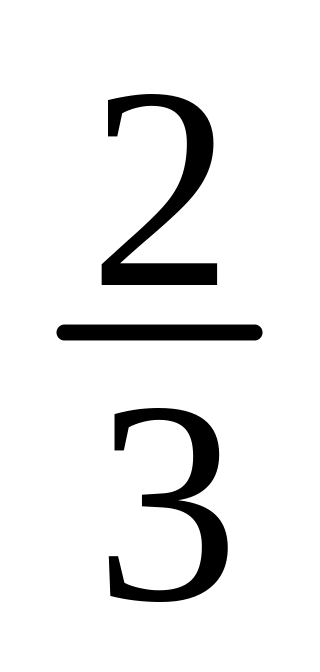 деталей бракованных, а в двух других
все доброкачественные. Найти вероятность
того, что: а) взятая деталь бракованная;
б) эта бракованная деталь из первой
партии.
деталей бракованных, а в двух других
все доброкачественные. Найти вероятность
того, что: а) взятая деталь бракованная;
б) эта бракованная деталь из первой
партии.Вероятность попадания при одном выстреле
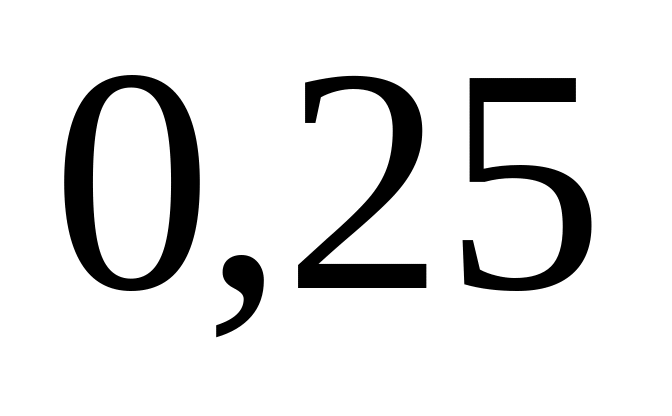 .
Найти вероятность, что будет не менее
трех попаданий при пяти независимых
выстрелах.
.
Найти вероятность, что будет не менее
трех попаданий при пяти независимых
выстрелах.Случайная величина
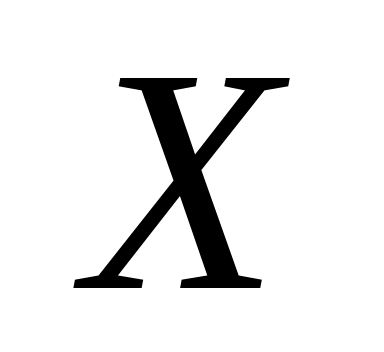 задана рядом распределения
задана рядом распределения
|
|
|
|
|
|
|
|
|
|
Найти 1)
,
2) функцию распределения
![]() и ее график; 3)
;
4)
;
5) СКВО, моду и медиану; 6)
и ее график; 3)
;
4)
;
5) СКВО, моду и медиану; 6) ![]() .
.
Задана функция распределения непрерывной случайной величины
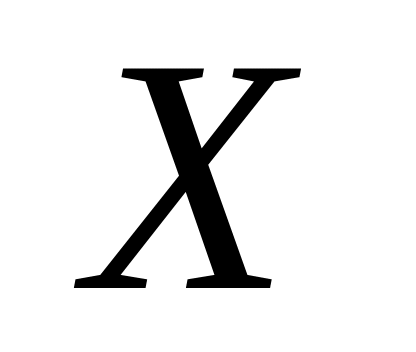
![]()
Найти:
![]() ,
,
,
СКВО, моду и медиану, плотность
распределения
,
,
,
СКВО, моду и медиану, плотность
распределения
![]() ,
,
![]() .
.
Каждый из
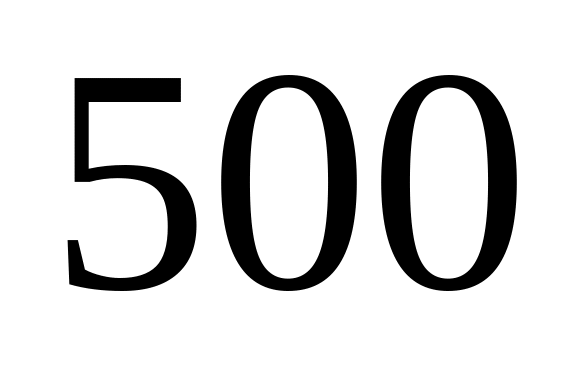 элементов выходит из строя в течение
минуты с вероятностью
элементов выходит из строя в течение
минуты с вероятностью
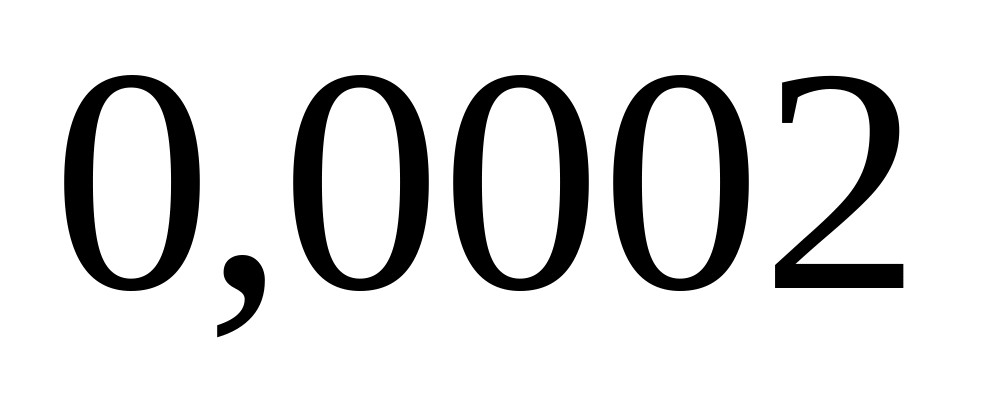 .
Какова вероятность, что за час выйдет
из строя не более двух элементов?
.
Какова вероятность, что за час выйдет
из строя не более двух элементов?Деталь удовлетворяет стандарту, если отклонение ее длины от нормы по абсолютной величине не более
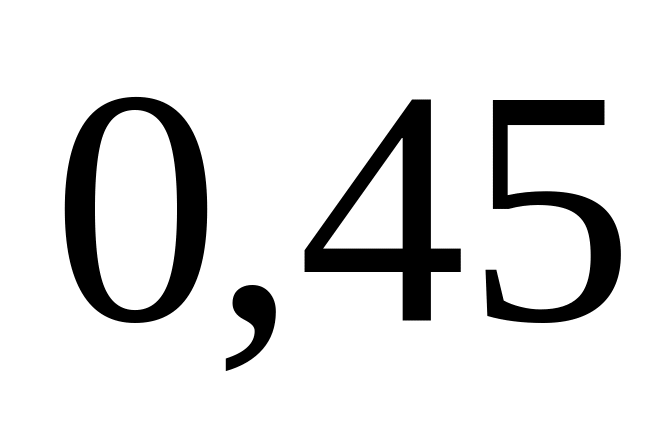 мм.
Случайное отклонение от нормы подчинено
нормальному закону с параметрами
мм.
Случайное отклонение от нормы подчинено
нормальному закону с параметрами
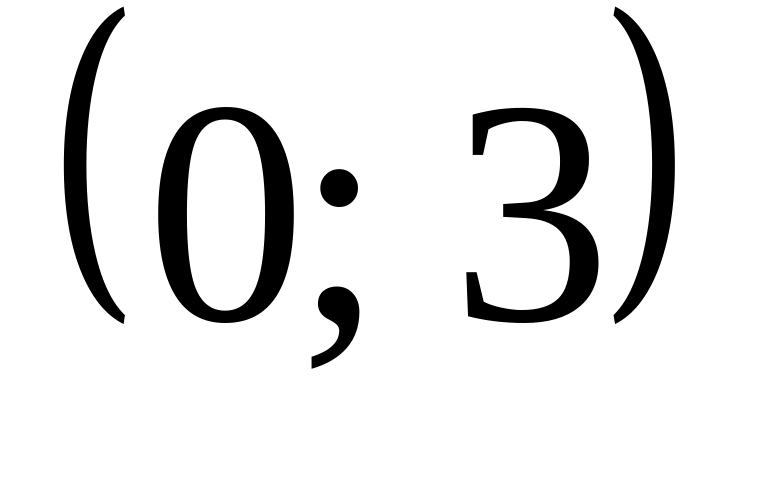 .
Определить среднее число стандартных
деталей, если изготовлено пять деталей.
Измерения длин деталей независимы.
.
Определить среднее число стандартных
деталей, если изготовлено пять деталей.
Измерения длин деталей независимы.
