
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Дана функция распределения непрерывной случайной величины
- •Вариант 6
- •Вариант 7
- •Дана функция распределения непрерывной случайной величины
- •Вариант 8
- •Дана функция распределения непрерывной случайной величины .
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Дана плотность распределения случайной величины
- •Вариант 12
- •Вариант 13
- •Дана плотность распределения случайной величины
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Задана функция распределения непрерывной случайной величины .
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Из колоды карт вынимают две карты. Событие – хотя бы одна карта черной масти; событие – обе карты черной масти. Что означают события
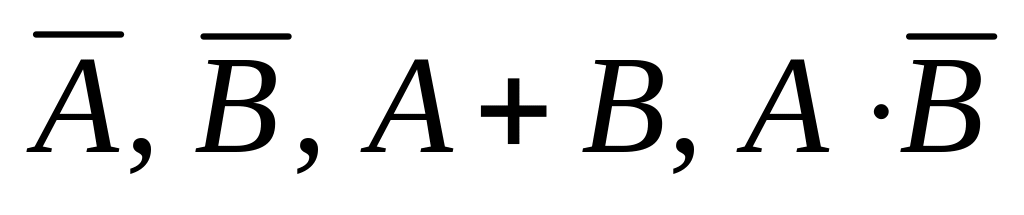 ?
?Числа
 расставлены случайным образом. Найти
вероятность того, что числа
и
расположены рядом.
расставлены случайным образом. Найти
вероятность того, что числа
и
расположены рядом.На отрезок
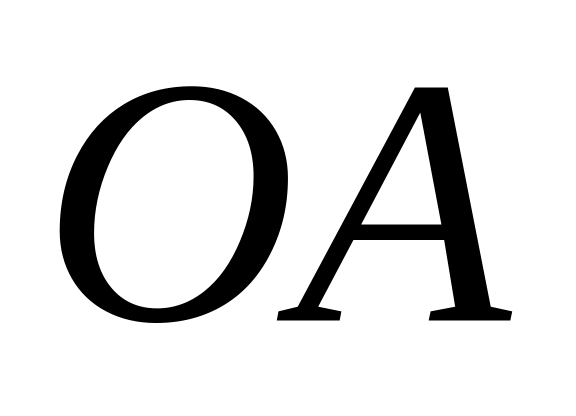 длины
длины
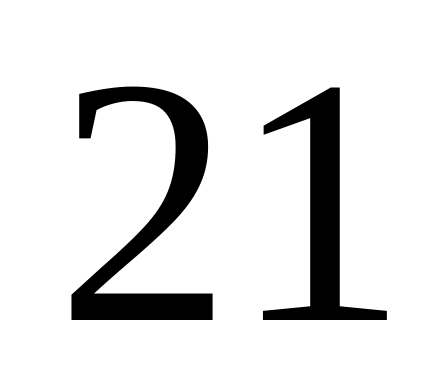 см наудачу бросается точка
.
Найти вероятность того, что меньший из
отрезков
см наудачу бросается точка
.
Найти вероятность того, что меньший из
отрезков
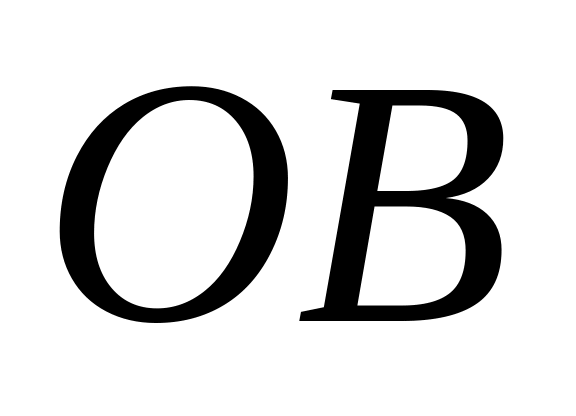 и
и
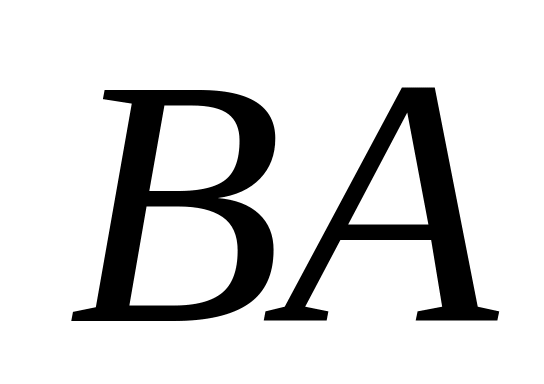 имеет длину, большую, чем
см.
имеет длину, большую, чем
см.В урне белых,
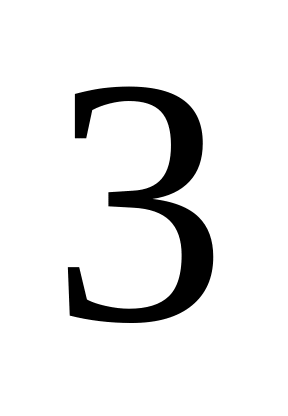 черных,
красных шаров. Вынимают по очереди три
шара. Определить вероятность того, что
последние два шара красные.
черных,
красных шаров. Вынимают по очереди три
шара. Определить вероятность того, что
последние два шара красные.В двух партиях
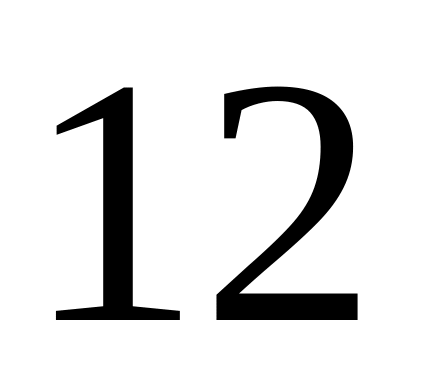 и
изделий, причём в каждой одно изделие
бракованное. Одно изделие из первой
партии переложили во вторую. а) Определить
вероятность того, что взятое после
этого из второй партии изделие –
бракованное; б) Взятое из второй
партии изделие оказалось бракованным.
Чему равна вероятность, что до этого в
нее было переложено из первой партии
также бракованное изделие?
и
изделий, причём в каждой одно изделие
бракованное. Одно изделие из первой
партии переложили во вторую. а) Определить
вероятность того, что взятое после
этого из второй партии изделие –
бракованное; б) Взятое из второй
партии изделие оказалось бракованным.
Чему равна вероятность, что до этого в
нее было переложено из первой партии
также бракованное изделие?Вероятность отказа каждого прибора при испытании не зависит от отказов остальных и равна . Испытано пять приборов. Найти вероятность того, что отказало не более одного прибора.
Случайная величина – число отказавших приборов в предыдущей задаче. Найти:1) ряд распределения; 2) функцию распределения и ее график; 3) ; 4) ; 5) СКВО, моду и медиану; 6)
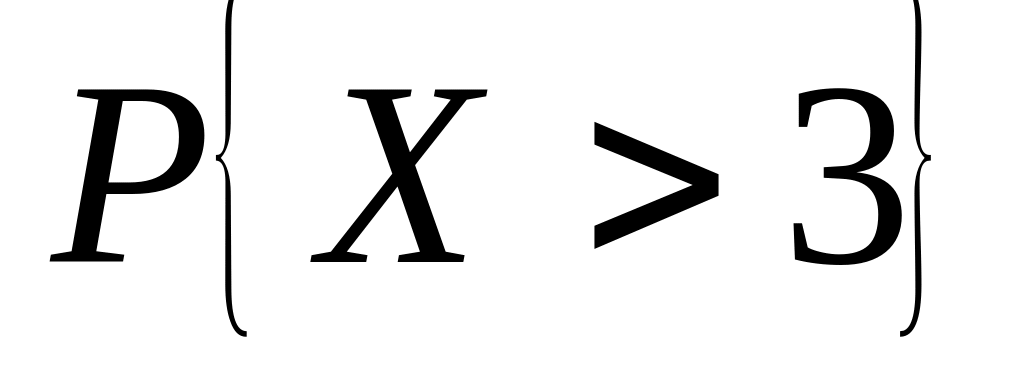 .
.Дана функция распределения непрерывной случайной величины
![]() .
.
Найти:
![]() ,
,
,
СКВО, моду и медиану, плотность
распределения
,
.
,
,
,
СКВО, моду и медиану, плотность
распределения
,
.
Проводятся испытания образцов на усталость. Вероятность поломки для каждого в течение суток
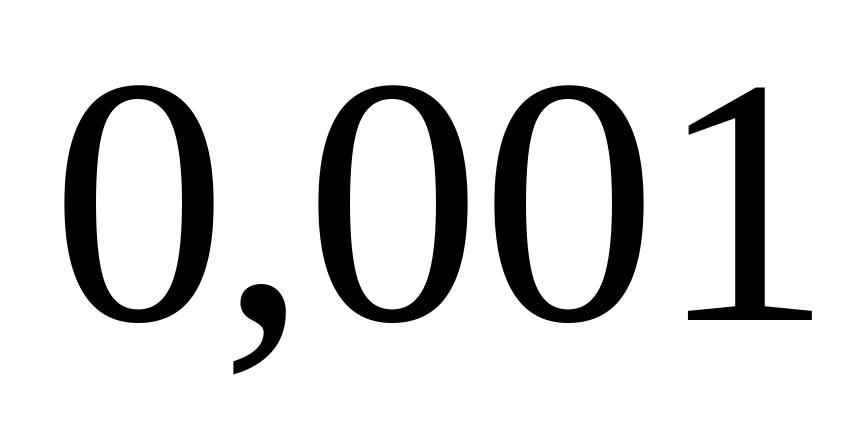 .
Найти вероятность того, что в течение
двух суток сломается менее двух образцов.
.
Найти вероятность того, что в течение
двух суток сломается менее двух образцов.Случайная величина , ошибка измерения диаметра вала, подчинена нормальному закону с параметрами . Найти вероятность того, что в двух независимых измерениях ошибка по абсолютной величине не менее мм.
Вариант 6
События – хотя бы один из трех проверяемых приборов бракованный, – все приборы доброкачественные. Что означают события
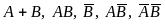 ?
?Имеется
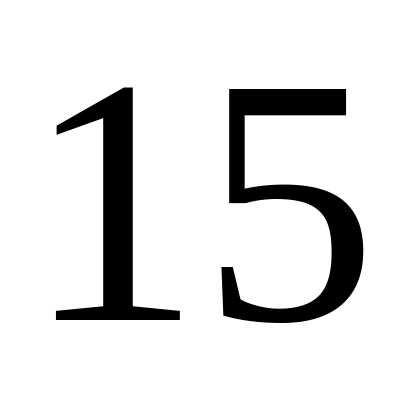 изделий, из них
бракованных. Для контроля наудачу
берутся
изделия. Определить вероятность того,
что а) брак не обнаружен; б) одно изделие
бракованное, другое нет.
изделий, из них
бракованных. Для контроля наудачу
берутся
изделия. Определить вероятность того,
что а) брак не обнаружен; б) одно изделие
бракованное, другое нет.На плоскость с нанесенной сеткой квадратов со стороной см наудачу бросают монету радиуса см. Найти вероятность того, что монета не пересчет ни одной из сторон квадрата.
При повышении напряжения в сети машина выходит из строя с вероятностью , а машина – с вероятностью . Определить вероятность того, что а) обе машины выйдут из строя; б) хотя бы одна из машин выйдет из строя, если они выходят из строя независимо друг от друга.
В первой урне белых и черных шаров, во второй – белых и черных. Из первой урны во вторую переложили один шар, затем из второй урны извлекли один шар. а) Определить вероятность того, что шар, извлеченный из второй урны, черный. б) Извлеченный из второй урны шар оказался черным. Какова вероятность, что до этого в нее был положен белый шар?
Вероятность сбоя в работе телефонной станции при каждом вызове . Определить вероятность того, что при пяти вызовах число сбоев не более двух.
Случайная величина – число сбоев в предыдущей задаче. Найти:1) ряд распределения; 2) функцию распределения и ее график; 3) ; 4) ; 5) СКВО, моду и медиану; 6)
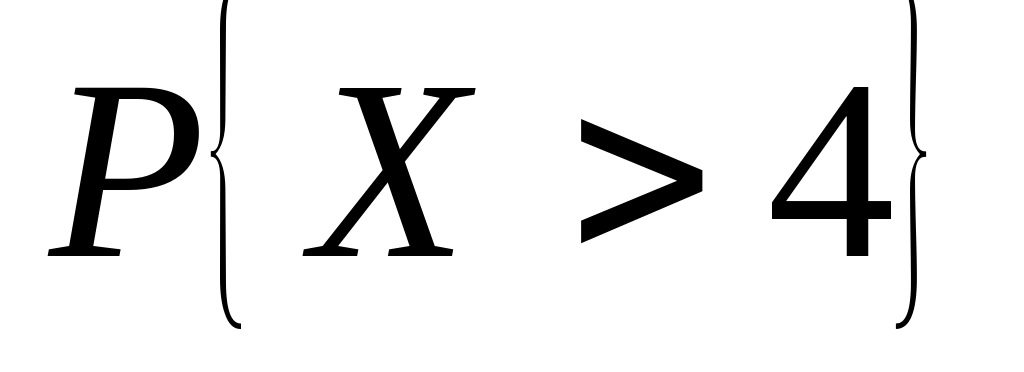 .
.Дана плотность распределения непрерывной случайной величины
![]() .
.
Найти:
,
,
,
моду и медиану, функцию распределения
,
![]() .
.
Сеанс дальней связи подводной лодки длится сек. При этом наблюдаются атмосферные помехи в среднем в час. Найти вероятность отсутствия помех во время сеанса подводной лодки.
Диаметр втулки распределен нормально с параметрами
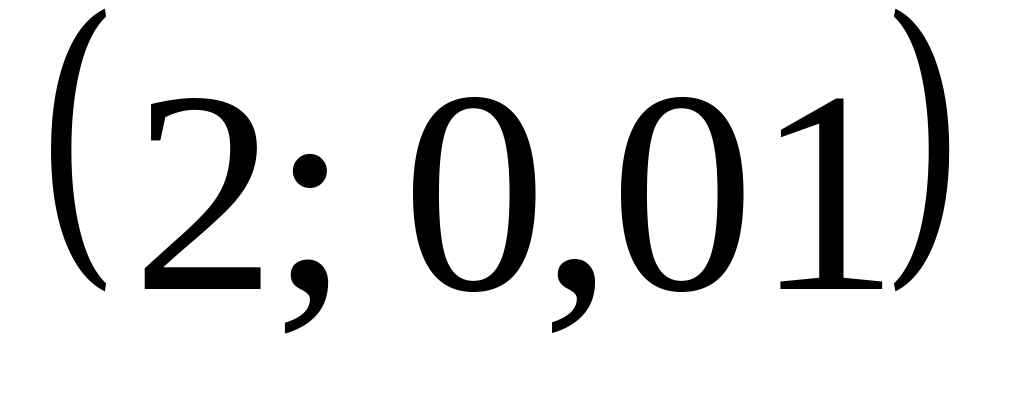 .
В каких границах можно практически
гарантировать диаметр втулки?
.
В каких границах можно практически
гарантировать диаметр втулки?
Вариант 7
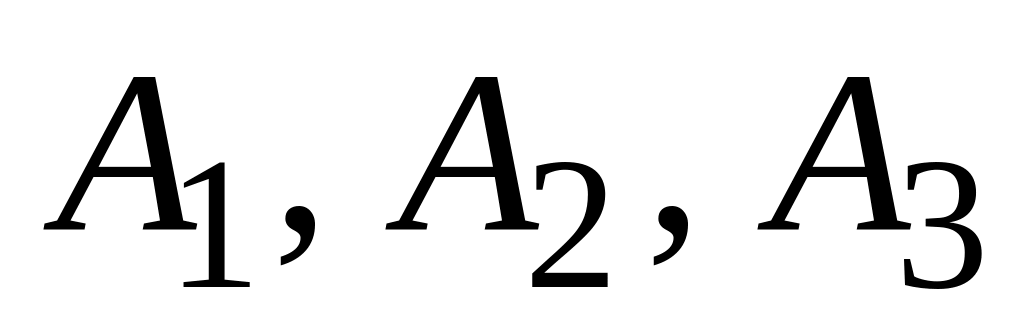 – некоторые
события. Найти выражение для событий:
– произошло два события из трех,
– ни одно из них не произошло.
– некоторые
события. Найти выражение для событий:
– произошло два события из трех,
– ни одно из них не произошло.Среди
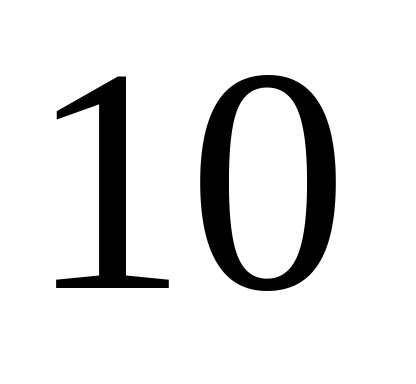 лотерейных билетов
лотерейных билетов
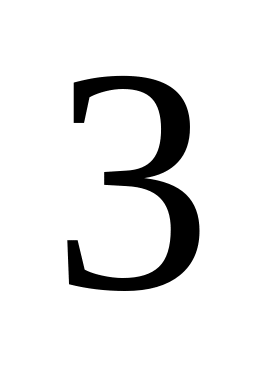 выигрышные. Наудачу взяли
выигрышные. Наудачу взяли
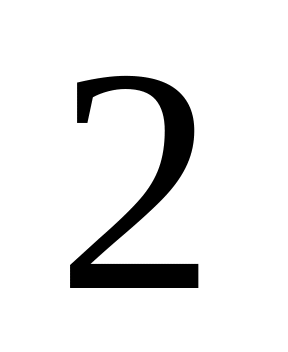 билета. Определить вероятность того,
что а) оба билета выиграли, б) один
выиграл, а другой нет.
билета. Определить вероятность того,
что а) оба билета выиграли, б) один
выиграл, а другой нет.Через точку на окружности радиуса
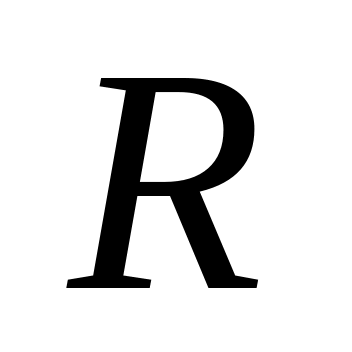 проводят хорды перпендикулярно диаметру.
Найти вероятность, что длина случайно
взятой хорды не более
проводят хорды перпендикулярно диаметру.
Найти вероятность, что длина случайно
взятой хорды не более
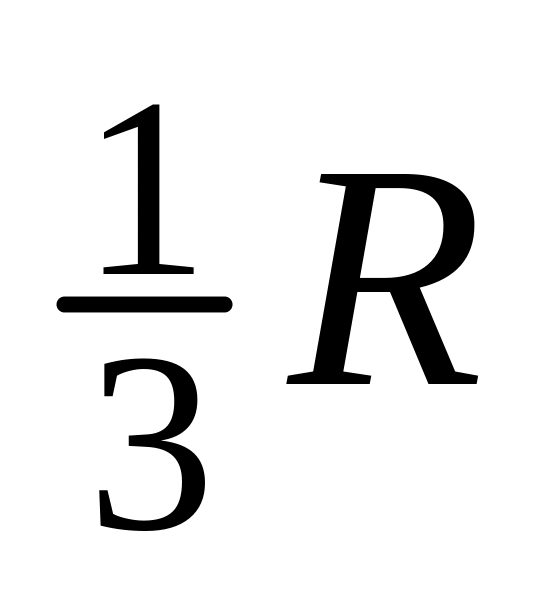 .
.Вероятность хотя бы одного попадания в цель при двух независимых выстрелах равна
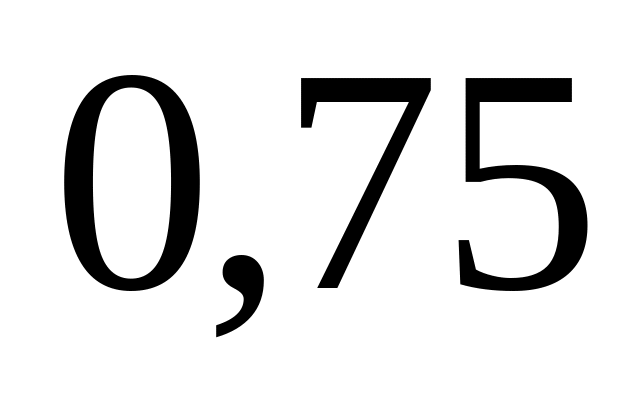 .
Найти вероятность двух попаданий при
двух выстрелах.
.
Найти вероятность двух попаданий при
двух выстрелах.Компьютерная фирма покупает дисководы CD-ROM двух производителей. Продукция первого производителя содержит в среднем
 %
брака, а второго –
%
брака. Фирма закупила
%
брака, а второго –
%
брака. Фирма закупила
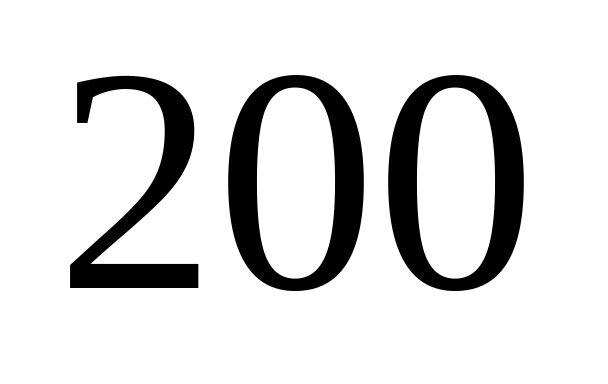 дисководов первого производителя и
дисководов первого производителя и
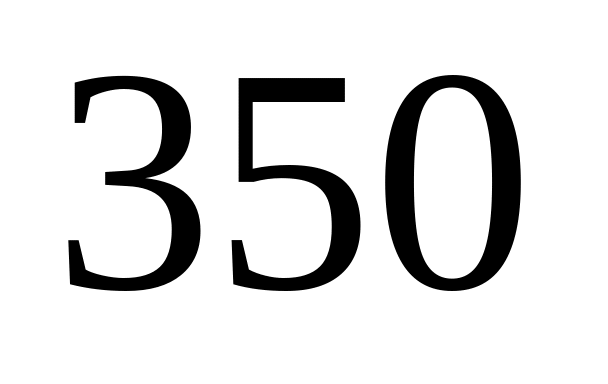 второго. Найти вероятности того, что:
а) один случайно купленный фирмой
дисковод оказался бракованным; б) этот
бракованный дисковод от первого
производителя.
второго. Найти вероятности того, что:
а) один случайно купленный фирмой
дисковод оказался бракованным; б) этот
бракованный дисковод от первого
производителя.Вероятность того, что при пяти независимых вызовах сбой в работе телефонной станции произойдет хотя бы раз
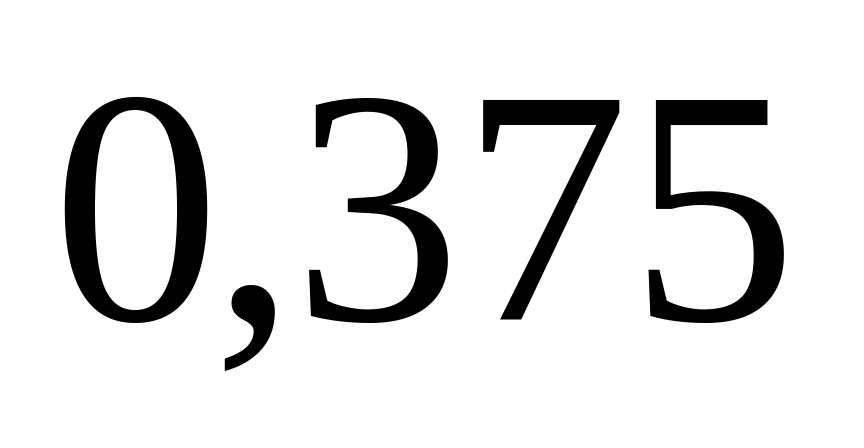 .
Найти вероятность сбоя при одном вызове,
если она одинакова при любом вызове.
.
Найти вероятность сбоя при одном вызове,
если она одинакова при любом вызове.Случайная величина задана рядом распределения
|
|
|
|
|
|
|
|
|
|
Найти:1) ряд
распределения; 2) функцию распределения
и ее график; 3) ![]() ;
4)
;
4) ![]() ;
5) СКВО, моду и медиану; 6)
;
5) СКВО, моду и медиану; 6) ![]() .
.
