Вариант 24

1. Поражение боевого самолёта (событие ) может наступить в результате поражения обоих двигателей (события 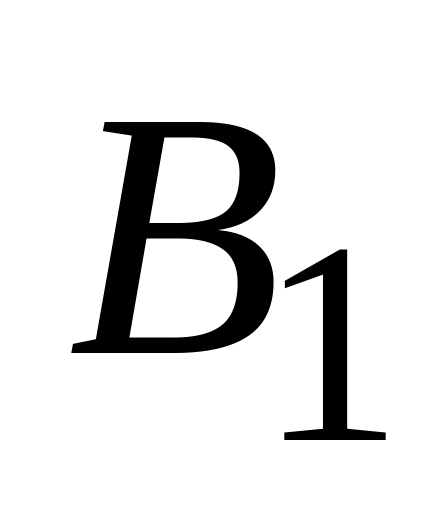и 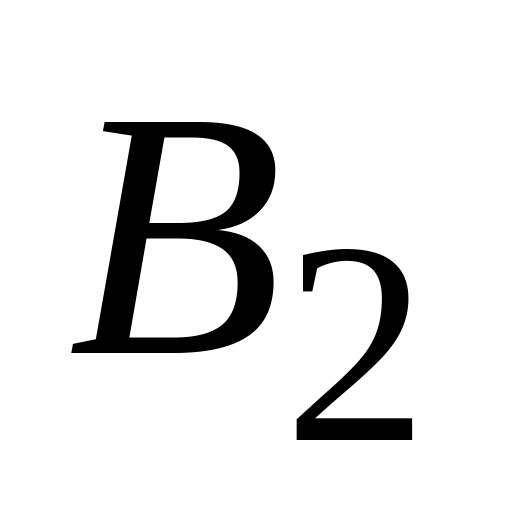) или в результате попадания в кабину пилота (событие ). Выразить событие через , , .

2. На семи карточках написаны буквы: А, Б, В, Г, Д, Е, Ж. Берутся по очереди четыре карточки. Определить вероятность того, что они образуют слово БЕДА.

3. Какова вероятность попасть, не целясь, бесконечно малой пулей в прутья квадратной решётки, если толщина прутьев , а расстояние между их осями , ?

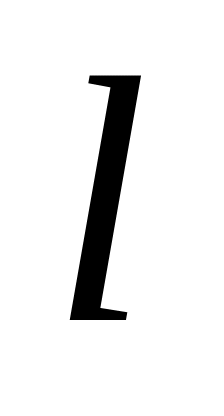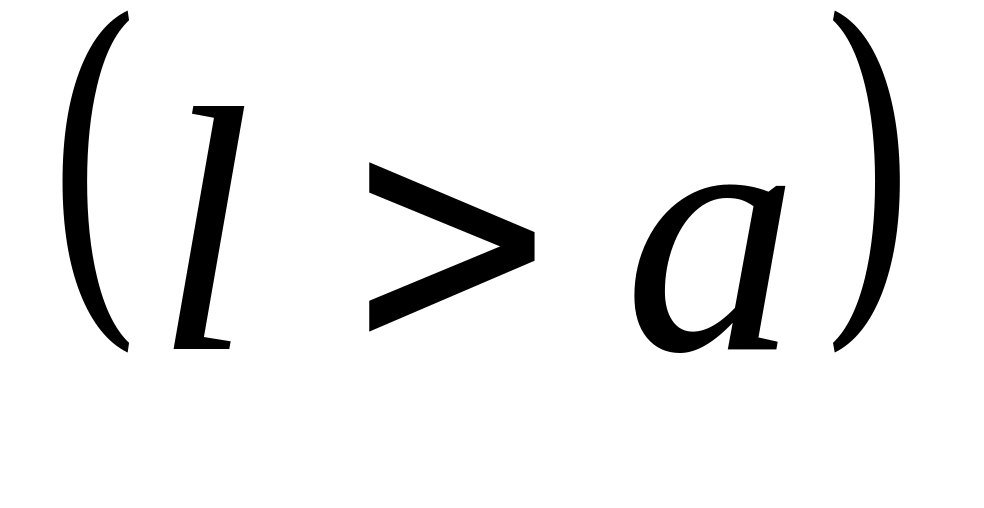4. В лотерее 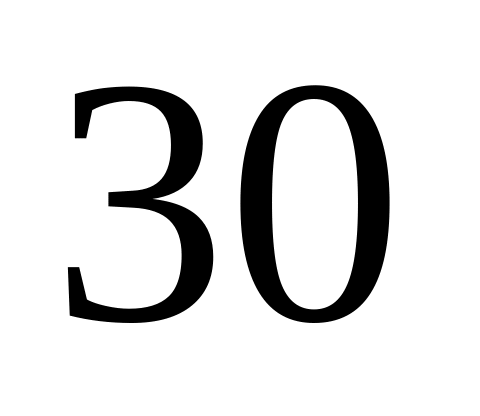билетов, из которых выигрышных. Какова вероятность выиграть, имея три билета?

5. После предварительного контроля деталь проходит одну из трех операций обработки с вероятностями 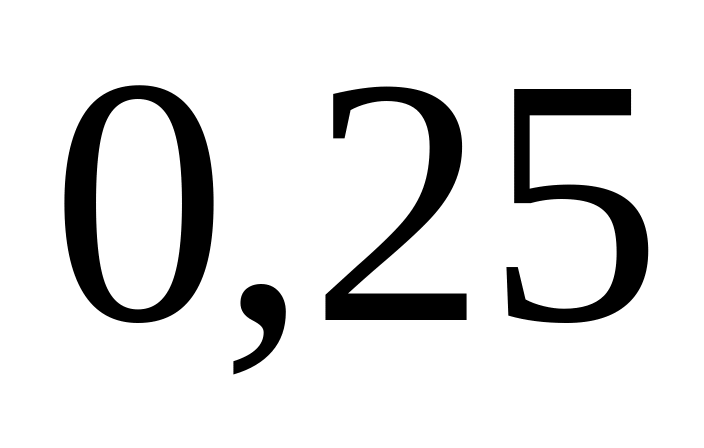, , 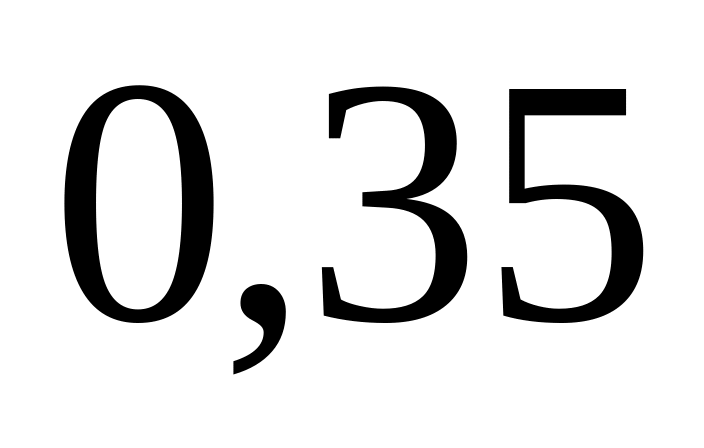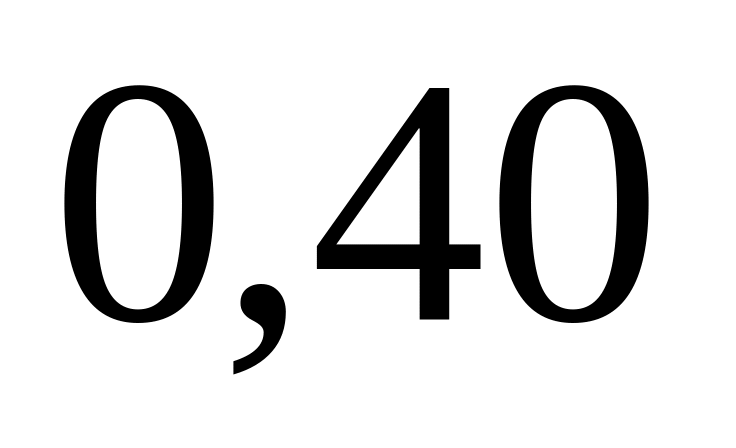соответственно. Вероятность получения брака на первой операции равна 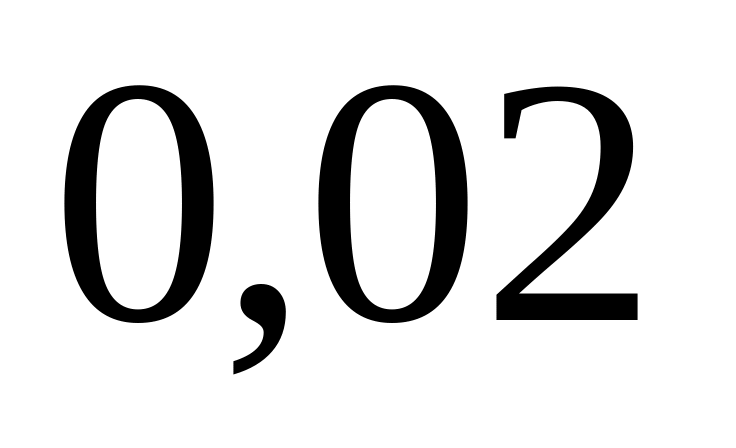; на второй – 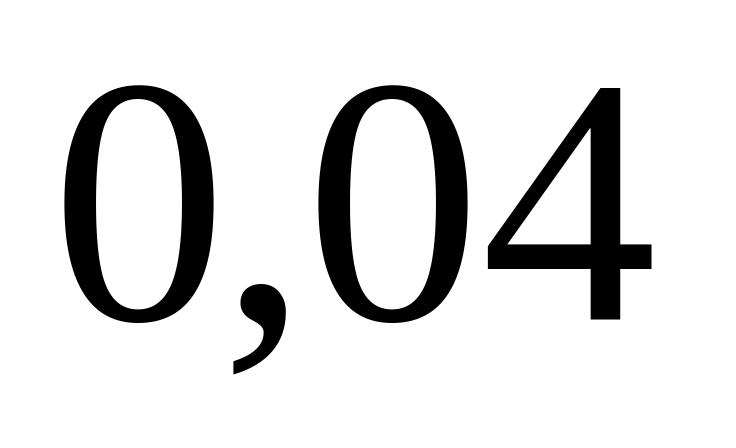; на третьей – . Найти вероятность того, что а) после обработки получена не бракованная деталь; б) эта не бракованная деталь обрабатывалась первой операцией.

6. При передачи сообщения вероятность искажения одного знака . Передано сообщение из пяти знаков. Найти вероятность того, что только один знак неверен.

7. Случайная величина – число искажений в предыдущей задаче. Найти 1) ряд распределения, 2) функцию распределения и ее график; 3)  ; 4)  ; 5) СКВО, моду и медиану; 6)  .

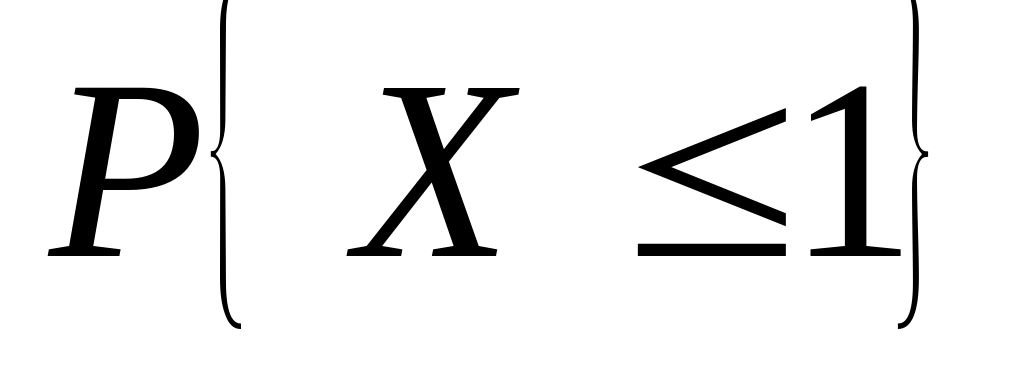8. Задана функция распределения случайной величины

.

Найти: , , , , СКВО, моду и медиану; плотность распределения , .

9. Сеанс дальней связи подводной лодки длится сек. Число помех в среднем 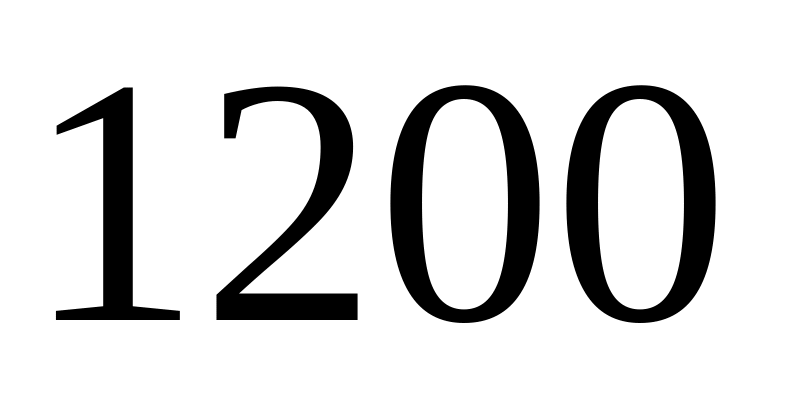в час. Какова вероятность, что за сеанс будет одна помеха?

10. Производится измерение диаметра вала. Случайна ошибка отклонения диаметра вала от нормы подчинена нормальному закону с параметрами 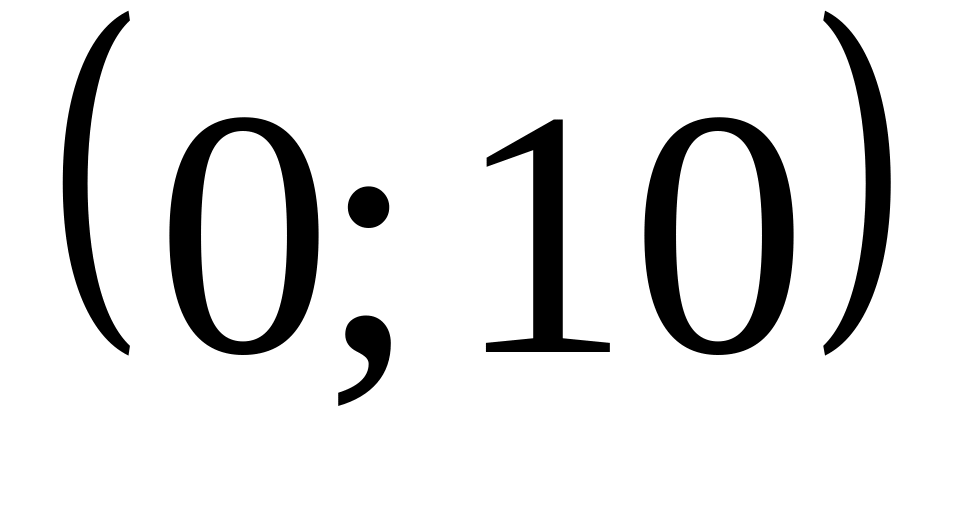. Каково должно быть отклонение по абсолютной величине от нормы, если вероятность того, что оно произошло равна ?

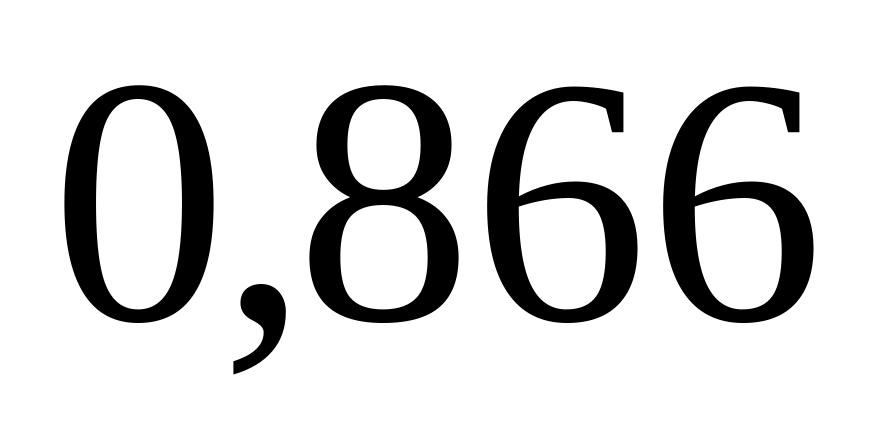Вариант 25

1. Два баскетболиста по очереди бросают мяч в корзину до первого попадания. Выигрывает тот, кто первый забросит мяч. События: – первый попадает при  – м броске;  –  второй попадает при  – м броске. Записать через и событие – выиграет первый.

2. Из множества натуральных чисел 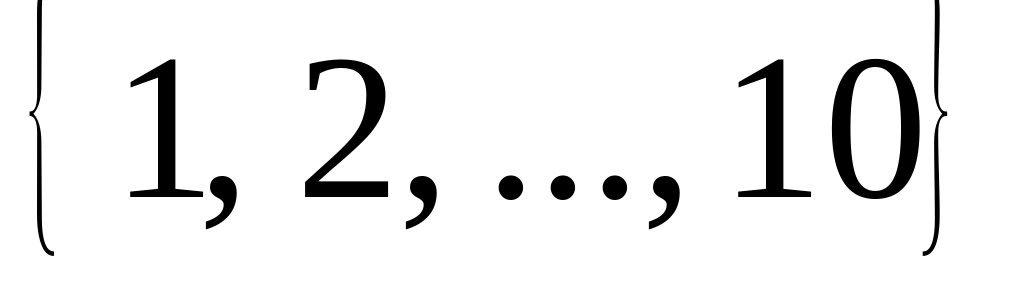случайно выбираются два числа. Найти вероятность того, что они оба простые.

3. Луч локатора перемещается с постоянной угловой скоростью в горизонтальной плоскости. Какова вероятность обнаружить цель в угловом секторе радиан?

4. В урне 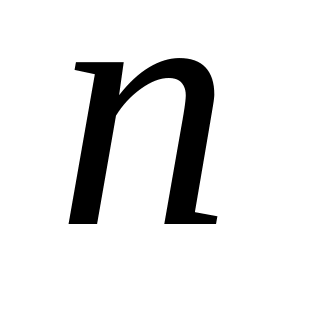шаров с номерами от до . Шары извлекают наудачу по одному без возвращения. Какова вероятность того, что при первых извлечениях номера шаров совпадут с номерами их извлечений.

5. Лотерея содержит выигрышных и невыигрышных билетов. Два билета продали. а) Найти вероятность того, что купленный после этого билет выигрышный. б) Купленный после этого билет оказался выигрышным. Какова вероятность т ого, что до этого купили не выигрышные билеты.

6. Из таблицы случайных чисел наугад выписано 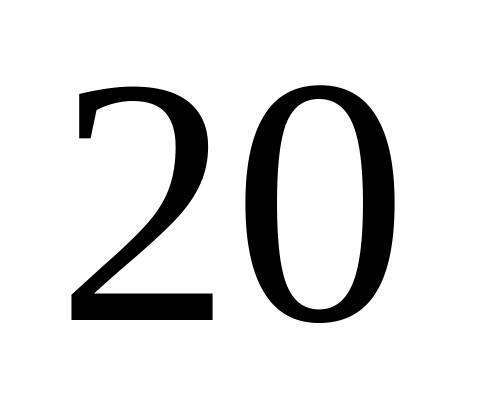двузначных чисел. Найти вероятность того, что среди них число встретится один раз.

7. Случайная величина задана рядом распределения

Найти 1)  , 2) функцию распределения и ее график; 3)  ; 4)  ; 5) СКВО, моду и медиану; 6)  .

8. Задана плотность распределения случайной величины

.

Найти: , , , СКВО, моду и медиану; функцию распределения , .

9. Проводятся испытания 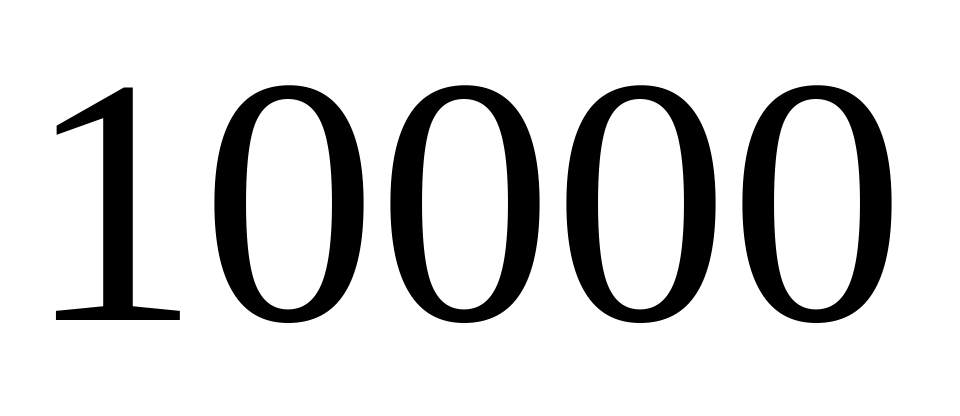образцов на усталость. Вероятность поломки одного образца за сутки мала. Найти эту вероятность, если вероятность того, что в течение трех суток сломается хотя бы один образец, равна .

10. Шлюпка бракуется, если толщина её обшивки более чем на  мм по абсолютной величине больше проектной. Отклонение подчинено нормальному закону с параметрами 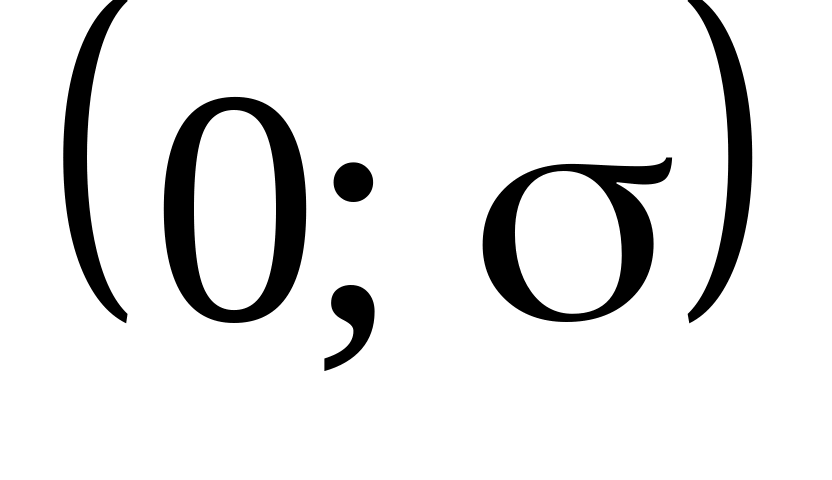. Найти , если вероятность того, что шлюпка забракована, равна .