
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Дана функция распределения непрерывной случайной величины
- •Вариант 6
- •Вариант 7
- •Дана функция распределения непрерывной случайной величины
- •Вариант 8
- •Дана функция распределения непрерывной случайной величины .
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Дана плотность распределения случайной величины
- •Вариант 12
- •Вариант 13
- •Дана плотность распределения случайной величины
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Задана функция распределения непрерывной случайной величины .
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
ТИПОВОЙ РАСЧЕТ
по теме "ТЕОРИЯ ВЕРОЯТНОСТЕЙ"
ДЛЯ ЭКОНОМИЧЕСКОГО ФАКУЛЬТЕТА
Вариант 1
Мишень состоит из трех кругов, образованных концентрическими окружностями. Событие
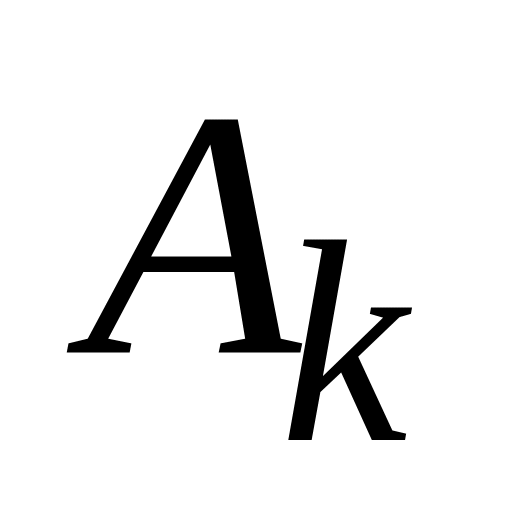 ,
,
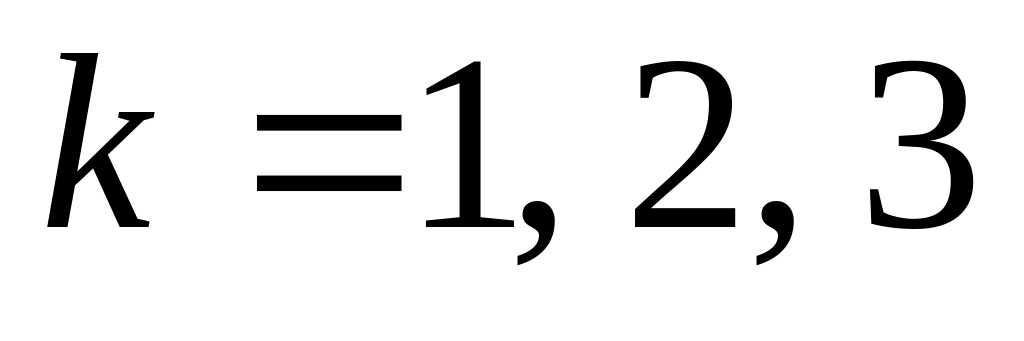 – попадание в круг радиуса
– попадание в круг радиуса
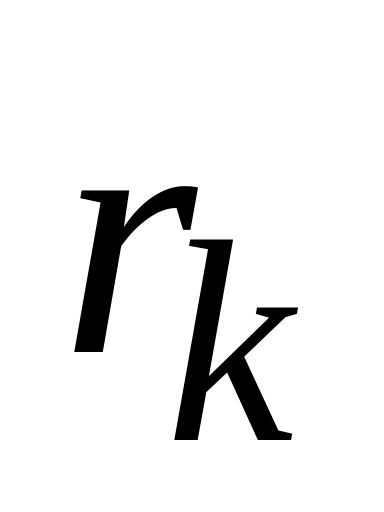 ,
,
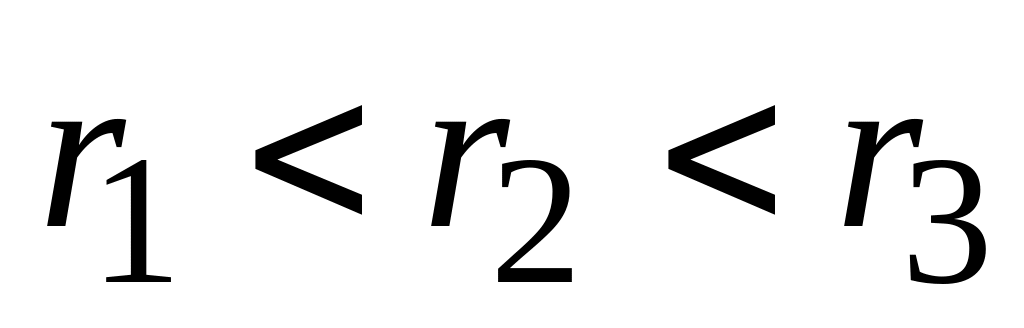 .
Что означают события:
.
Что означают события:
 ,
,
 ,
,
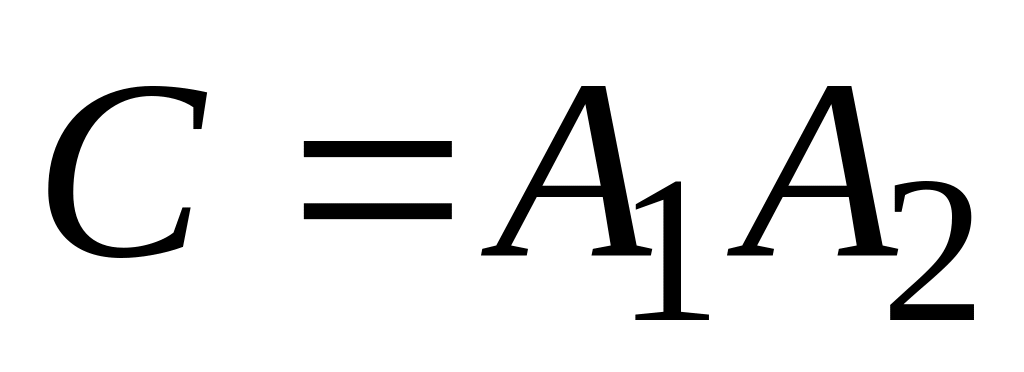 ?
?Номер состоит из шести цифр. Определить вероятность того, что а) все числа номера различны; б) номер делится на пять.
Какова вероятность того, что сумма двух наудачу взятых отрезков, длина которых не превосходит
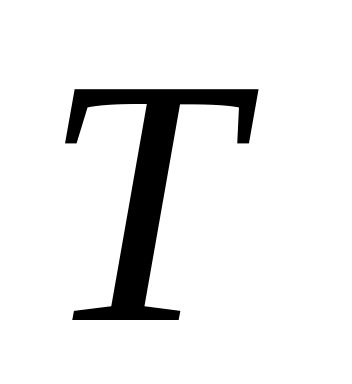 ,
будет больше
?
,
будет больше
?Из трех орудий произведен залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия
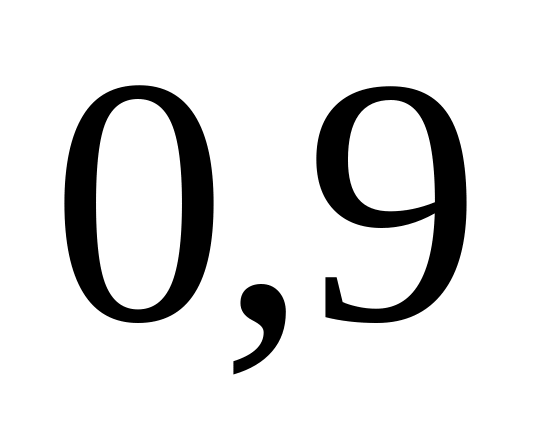 ,
из второго
,
из второго
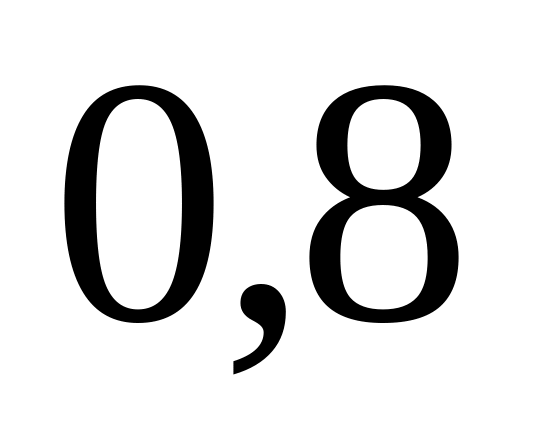 ,
из третьего
,
из третьего
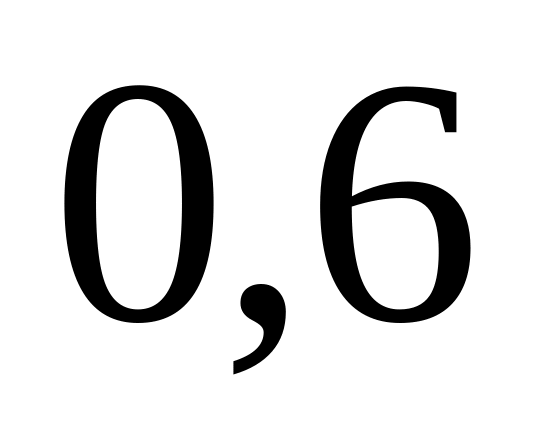 .
Найти вероятность, что только одно
орудие попадет в цель.
.
Найти вероятность, что только одно
орудие попадет в цель.В первой урне
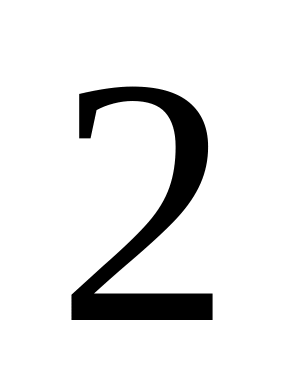 белых и
белых и
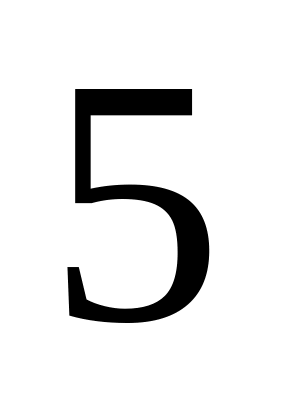 черных шаров, во второй –
белых и
черных. Из первой урны во вторую
переложили один шар, затем из второй
урны извлекли один шар. а) Определить
вероятность того, что, взятый из второй
урны шар – белый; б) Взятый из второй
урны шар оказался белым. Найти вероятность,
что до этого из первой урны во вторую
был переложен белый шар.
черных шаров, во второй –
белых и
черных. Из первой урны во вторую
переложили один шар, затем из второй
урны извлекли один шар. а) Определить
вероятность того, что, взятый из второй
урны шар – белый; б) Взятый из второй
урны шар оказался белым. Найти вероятность,
что до этого из первой урны во вторую
был переложен белый шар.Вероятность сбоя на телефонной станции при каждом вызове равна
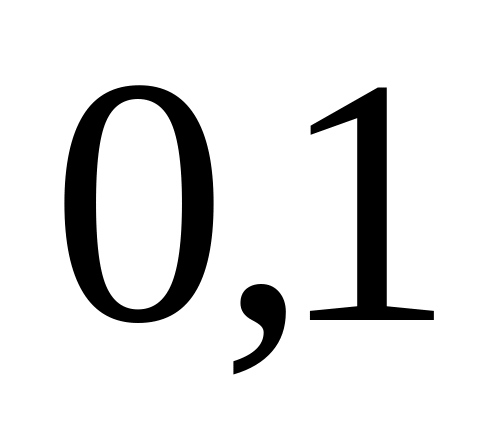 .
Поступило
вызовов. Найти вероятность того, что
было три сбоя.
.
Поступило
вызовов. Найти вероятность того, что
было три сбоя.Дискретная случайная величина
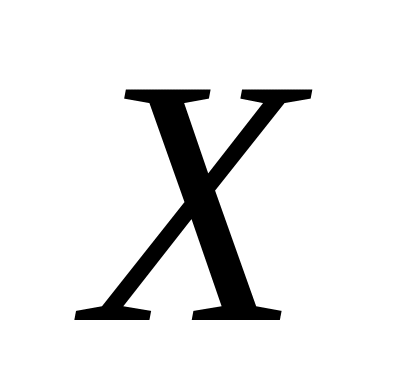 – число сбоев в предыдущей задаче.
Найти: 1) ряд распределения; 2) функцию
распределения
– число сбоев в предыдущей задаче.
Найти: 1) ряд распределения; 2) функцию
распределения
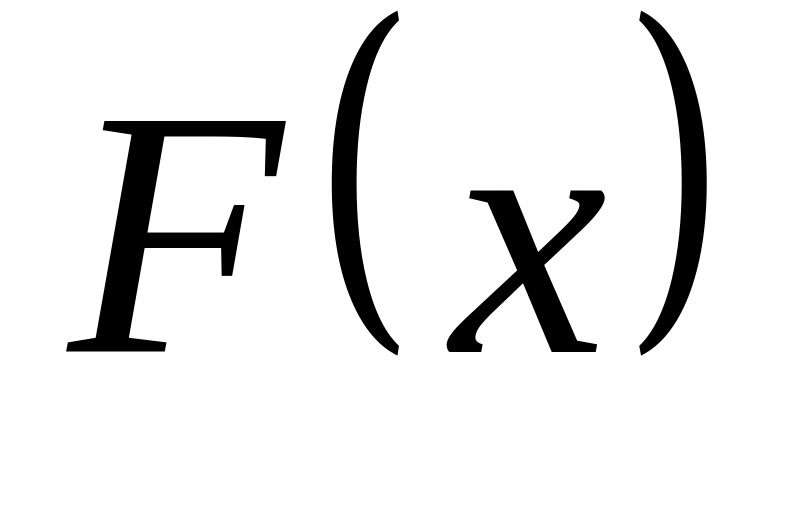 и ее график; 3)
и ее график; 3)  ;
4)
;
4) 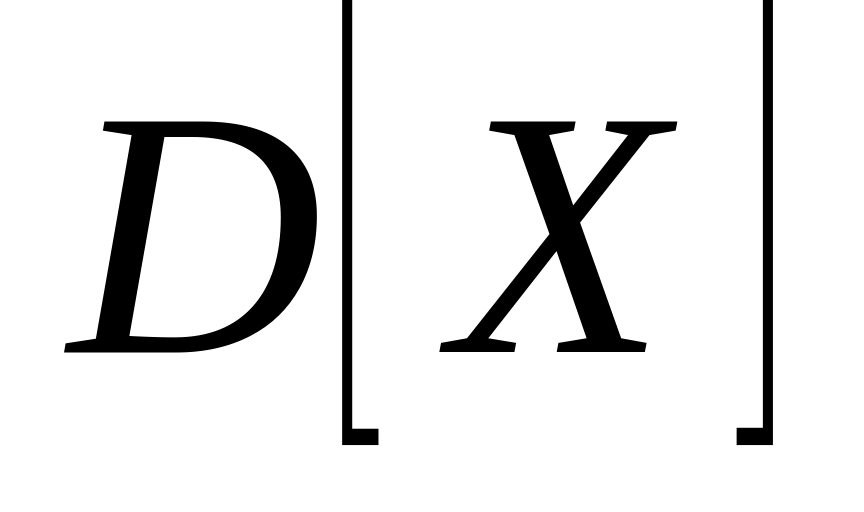 ;
5) СКВО, моду и медиану; 6)
;
5) СКВО, моду и медиану; 6)  .
.Дана функция распределения непрерывной случайной величины .
![]()
Найти:
![]() ,
,
![]() ,
,
,
СКВО, моду и медиану, плотность
распределения
,
,
,
СКВО, моду и медиану, плотность
распределения
![]() ,
,
![]() .
.
Поступление информации о результатах торгов на фондовой бирже подчиняется закону Пуассона со средним числом сообщений
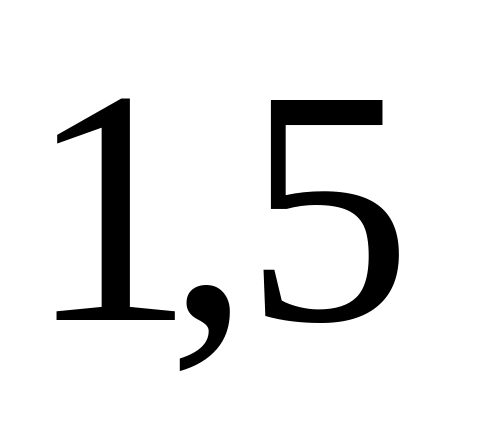 в минуту. Найти вероятность, что за
в минуту. Найти вероятность, что за
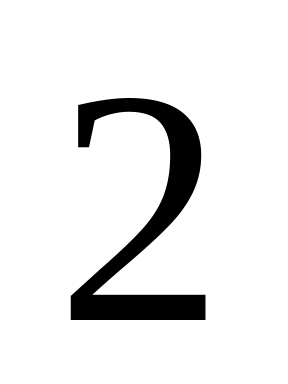 минуты не поступит ни одного сообщения.
минуты не поступит ни одного сообщения.Случайная величина – ошибка измерения диаметра вала, подчинена нормальному закону с параметрами
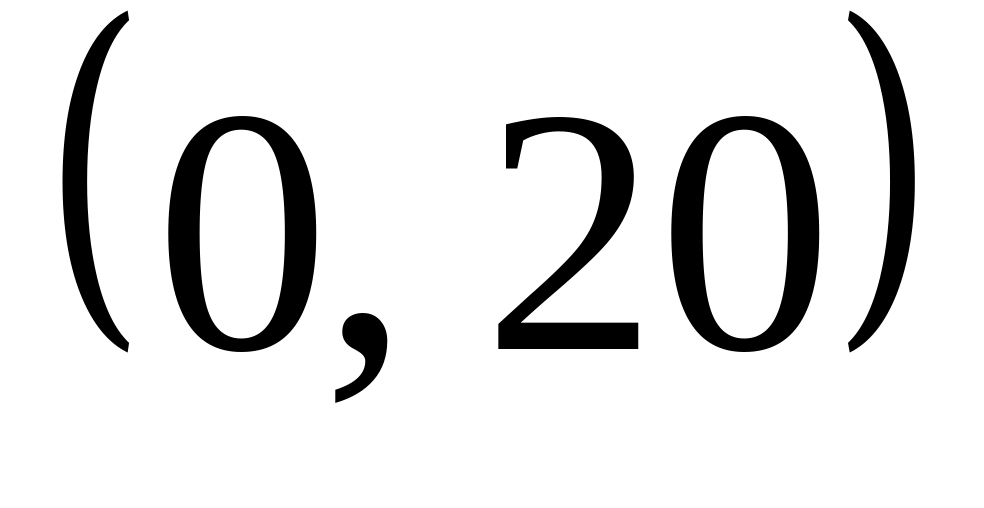 .
Найти вероятность того, что при трех
независимых измерениях ошибка хотя бы
одного не превзойдет по абсолютной
величине
.
Найти вероятность того, что при трех
независимых измерениях ошибка хотя бы
одного не превзойдет по абсолютной
величине
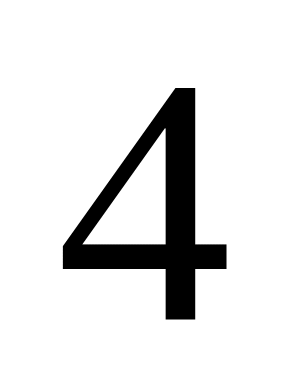 мм.
мм.
Вариант 2
Из таблицы случайных чисел наудачу взято число. Рассмотрим два события: – число делится на ;
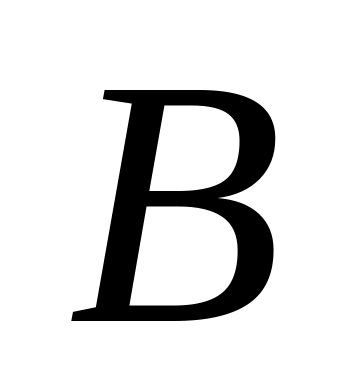 – число оканчивается нулем. Что означают
события
– число оканчивается нулем. Что означают
события
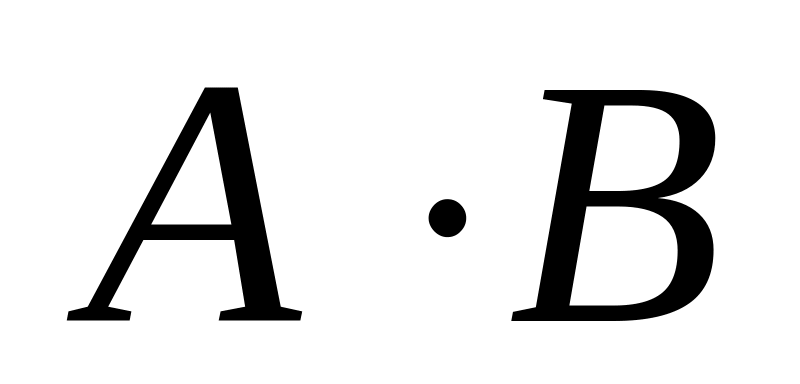 ;
;
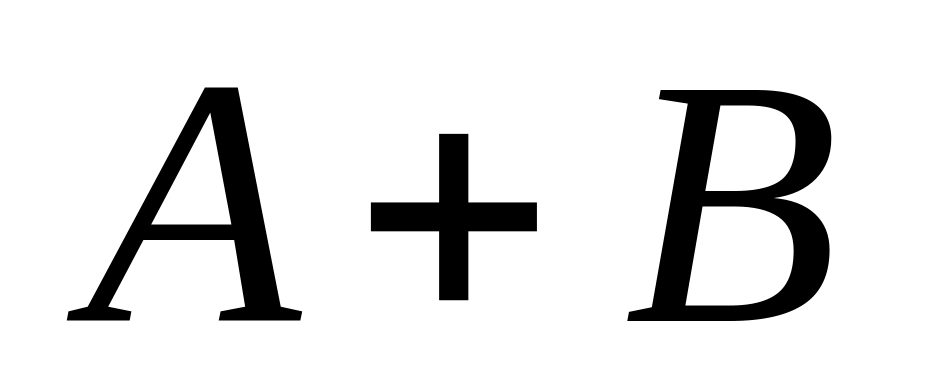 ;
;
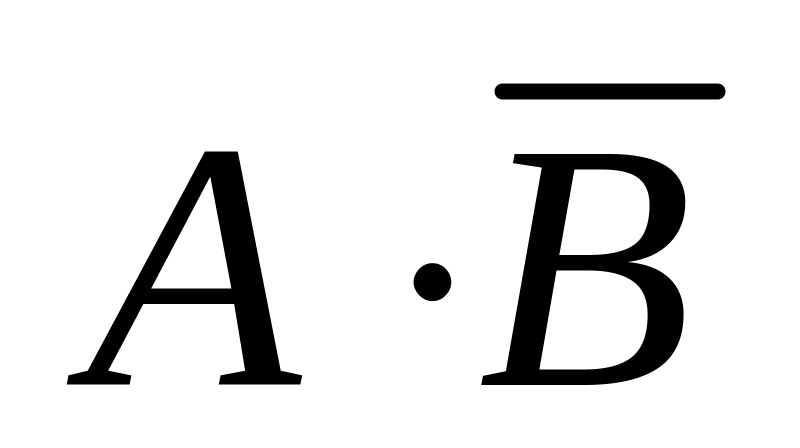 ;
;
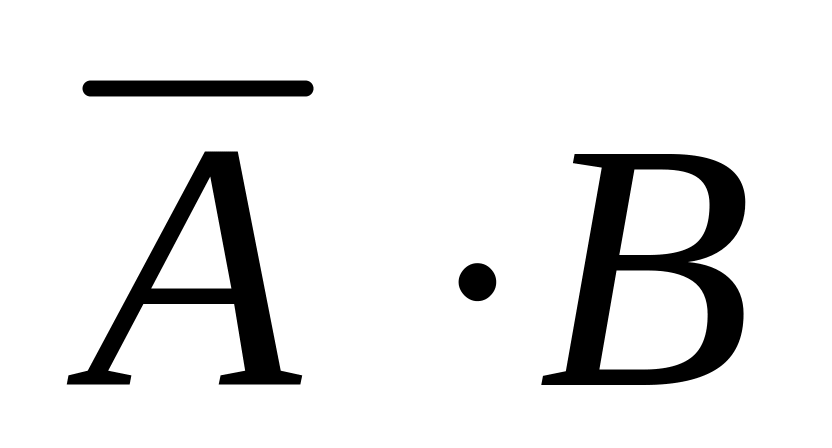 ;
;
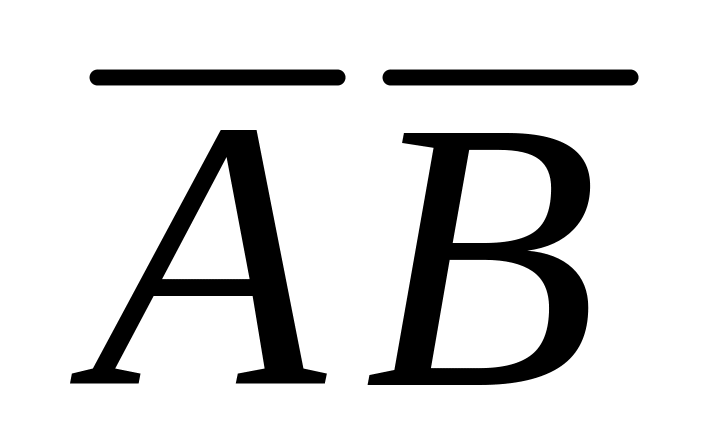 ?
?Урна содержит
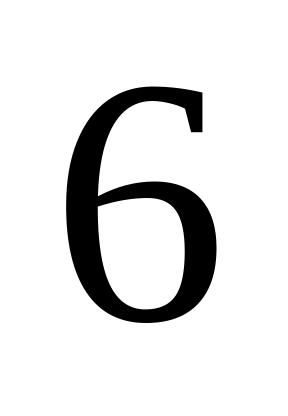 белых и
черных шара. Одновременно извлекаются
два шара, Определить вероятность того,
что а) оба шара черные; б) один черный,
другой белый.
белых и
черных шара. Одновременно извлекаются
два шара, Определить вероятность того,
что а) оба шара черные; б) один черный,
другой белый.Значения
 и
и
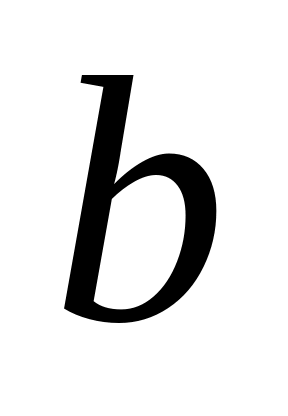 равновозможны в квадрате
равновозможны в квадрате
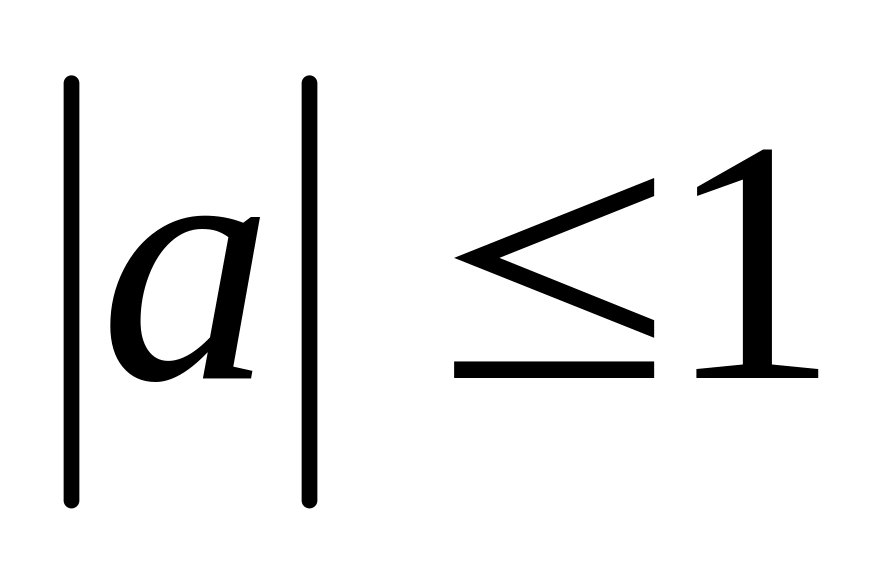 ,
,
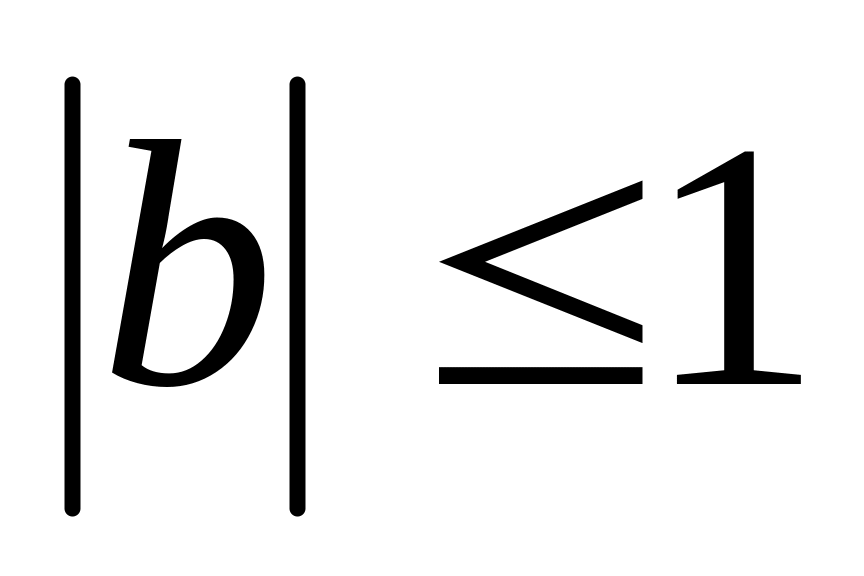 .
Найти вероятность того, что корни
квадратного трехчлена
.
Найти вероятность того, что корни
квадратного трехчлена
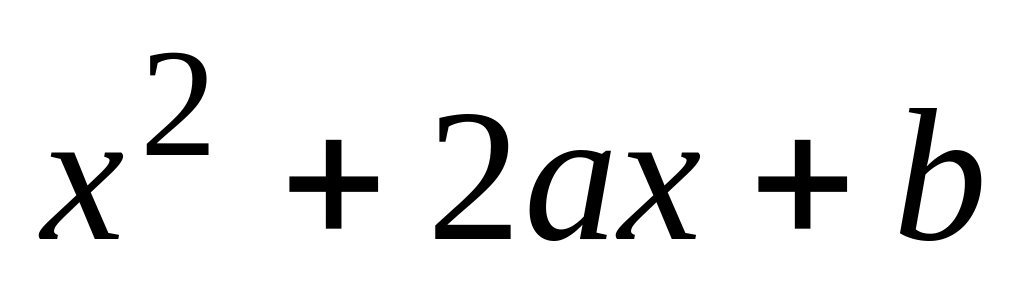 действительны.
действительны.Абонент забыл последнюю цифру номера телефона и потому набирает ее наудачу. Определить вероятность того, что ему придется звонить не более чем, в три места.
Из
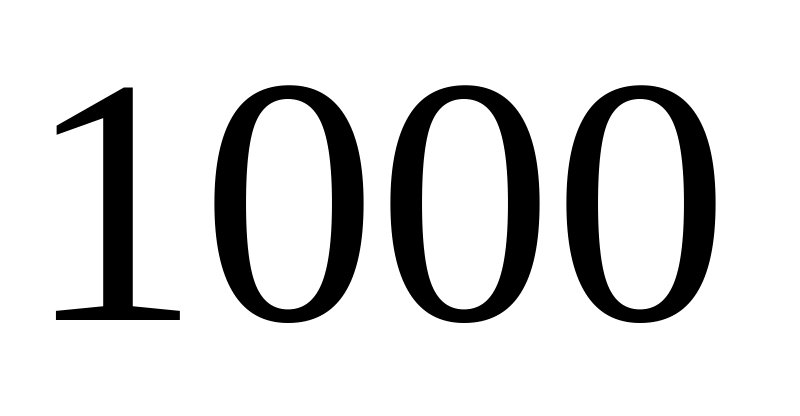 ламп
ламп
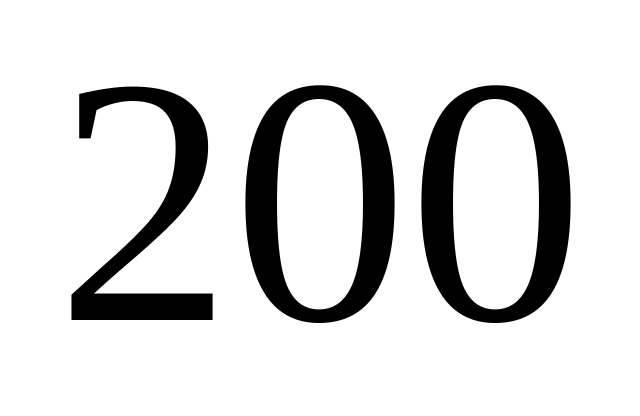 принадлежит первой партии,
принадлежит первой партии,
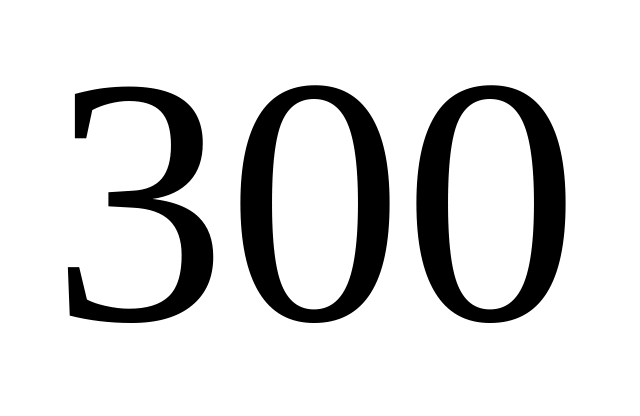 – второй,
– второй,
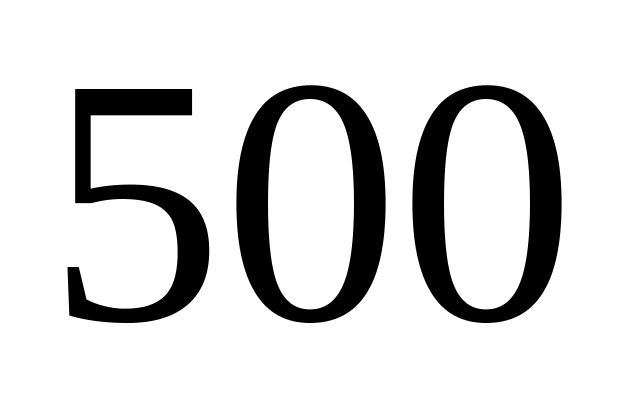 – третьей. В первой партии
– третьей. В первой партии
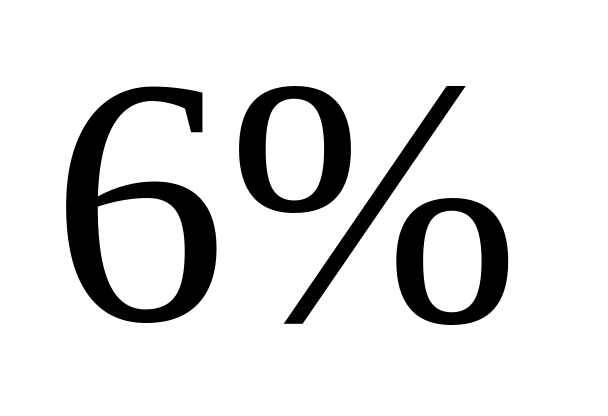 ,
во второй
,
во второй
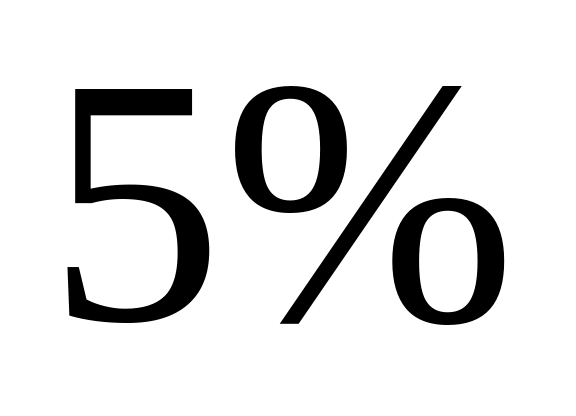 ,
а в
третьей
,
а в
третьей
 бракованных ламп. Определить вероятность
того, что: а) наудачу выбранная лампа
– бракованная; б) выбранная бракованная
лампа принадлежит третьей партии.
бракованных ламп. Определить вероятность
того, что: а) наудачу выбранная лампа
– бракованная; б) выбранная бракованная
лампа принадлежит третьей партии.Три монеты одновременно подбрасываются три раза. Определить вероятность того, что ровно в одном подбрасывании появится три "герба".
Дискретная случайная величина – появление трех "гербов" в предыдущей задаче. Найти: 1) ряд распределения; 2) функцию распределения и ее график; 3) ; 4) ; 5) СКВО, моду и медиану; 6)
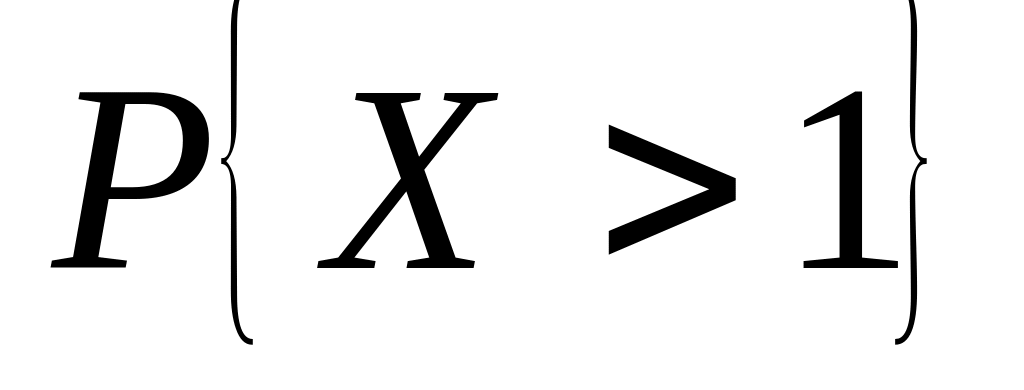 .
.Дана плотность распределения случайной величины
![]() .
.
Найти:
,
,
,
СКВО, моду и медиану, функцию распределения
,
![]() .
.
Поступление информации о результатах торгов на фондовой бирже подчиняется закону Пуассона со средним числом сообщений в минуту. Найти вероятность, что за минуты поступит пять сообщений.
Производится взвешивание вещества. Случайная ошибка взвешивания подчинена нормальному закону с параметрами
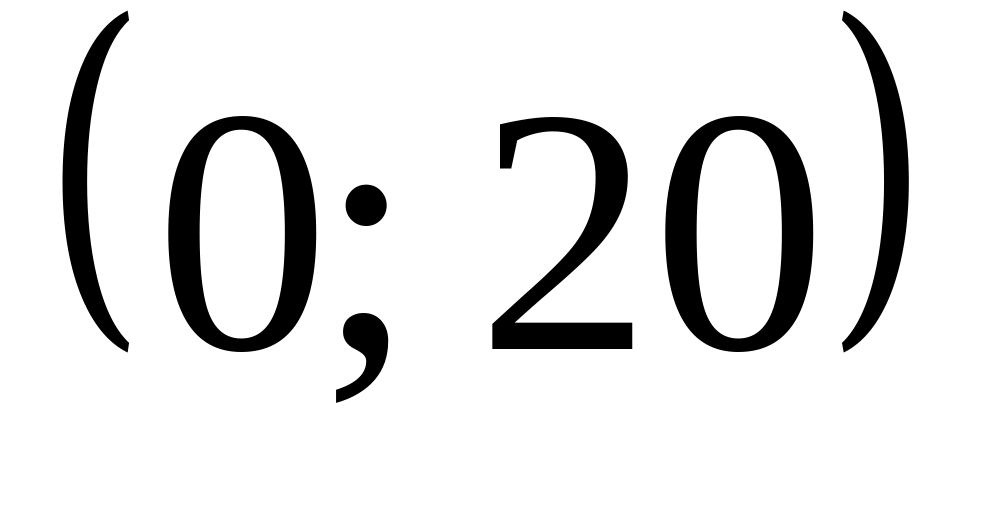 .
Определить вероятность того, что при
трех независимых взвешиваниях только
в одном ошибка по абсолютной величине
не превосходит
.
Определить вероятность того, что при
трех независимых взвешиваниях только
в одном ошибка по абсолютной величине
не превосходит
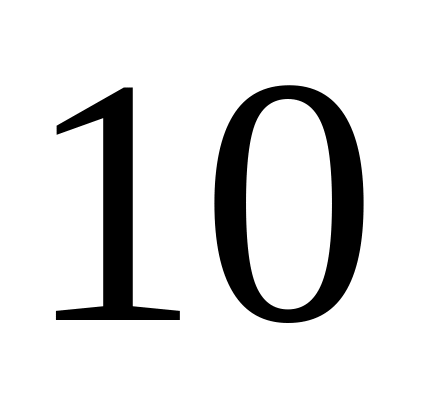 г.
г.
Вариант 3
Рабочий берет три детали из ящика. Событие – хотя бы одна из трех деталей бракованная; – не менее двух деталей из трех бракованные. Что означают события
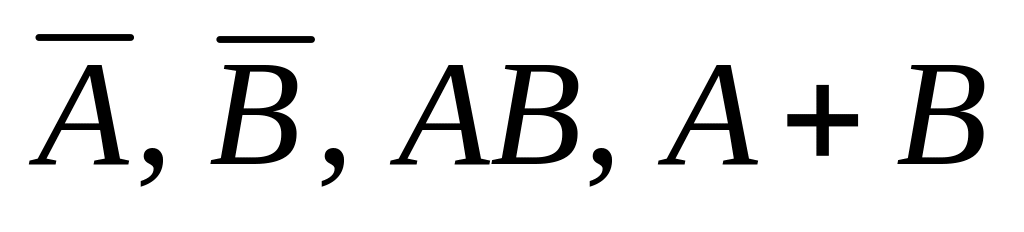 ?
?В группе из
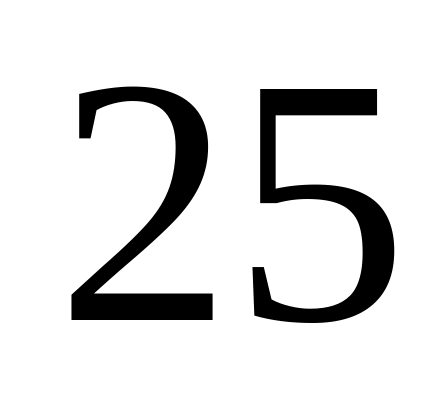 студентов
студентов
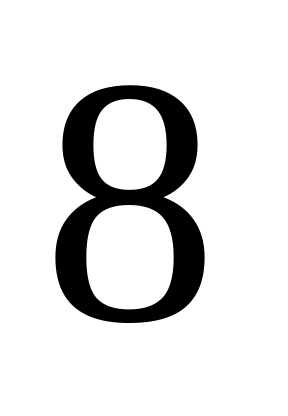 учатся отлично,
учатся отлично,
 хорошо,
удовлетворительно,
плохо. Преподаватель вызвал к доске
наугад
двух студентов. Определить вероятность
того, что а) оба учатся отлично; б) один
учится отлично, другой – плохо.
хорошо,
удовлетворительно,
плохо. Преподаватель вызвал к доске
наугад
двух студентов. Определить вероятность
того, что а) оба учатся отлично; б) один
учится отлично, другой – плохо.Наудачу взяты два положительных числа, каждое из которых не превышает двух. Определить вероятность того, что и их сумма не превышает двух.
В первой урне белых,
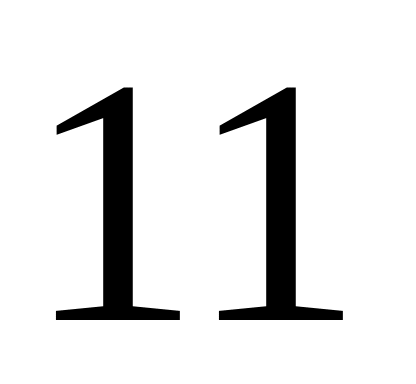 черных,
красных шаров, Во второй их соответственно
,
,
.
Из обеих урн извлекают по одному шару.
Какова вероятность, что оба шара одного
цвета?
черных,
красных шаров, Во второй их соответственно
,
,
.
Из обеих урн извлекают по одному шару.
Какова вероятность, что оба шара одного
цвета?В альбоме чистых и гашеных марок. Из них наугад берут одну марку, подвергают ее специальному гашению и возвращают в альбом. После этого снова берут одну марку. а) Определить вероятность того, что она чистая; б) Взятая вторая марка оказалась чистой. Чему равна вероятность, что до этого была погашена чистая марка.
Вероятность поражения крейсера торпедой равна
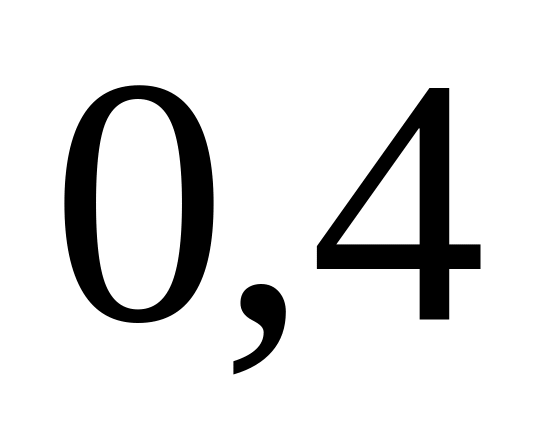 .
Произведено четыре залпа. Определить
вероятность того, что крейсер остался
невредим.
.
Произведено четыре залпа. Определить
вероятность того, что крейсер остался
невредим.Случайная величина – число попаданий в предыдущей задаче. Найти: 1) ряд распределения; 2) функцию распределения и ее график; 3) ; 4) ; 5) СКВО, моду и медиану; 6)
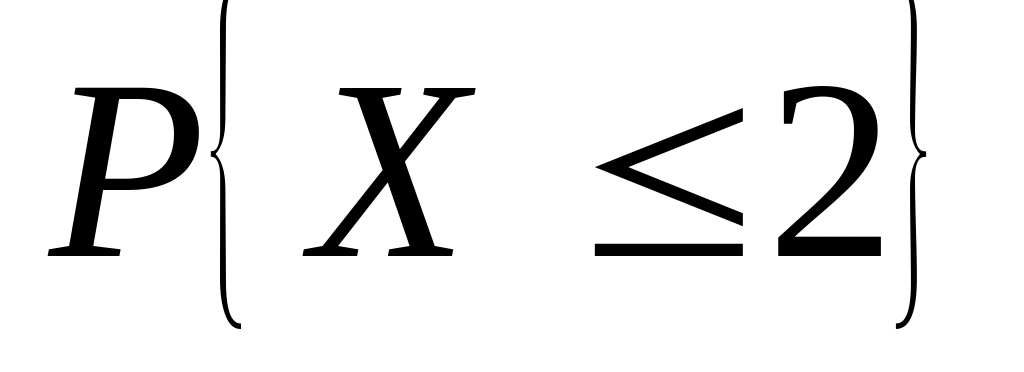 .
.Задана функция распределения непрерывной случайной величины
![]() .
.
Найти:
,
,
,
СКВО, моду и медиану, плотность
распределения
,
![]() .
.
Среднее число вызовов, полученных телефонисткой в час равно
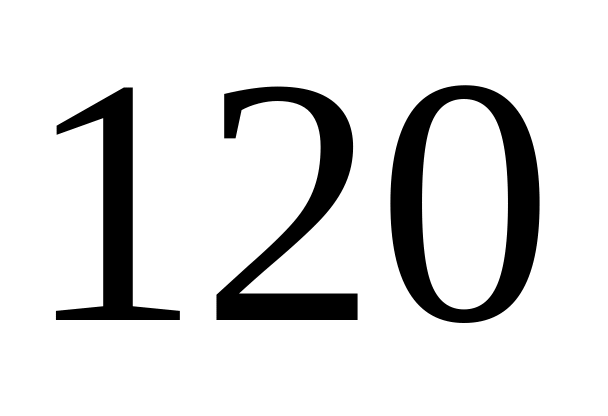 .
Какова вероятность, что в ближайшую
минуту она не получит вызов?
.
Какова вероятность, что в ближайшую
минуту она не получит вызов?Автомат изготовляет шарики. Шарик считается годным, если отклонение диаметра шарика от проектного размера (случайная величина ) по абсолютной величине меньше
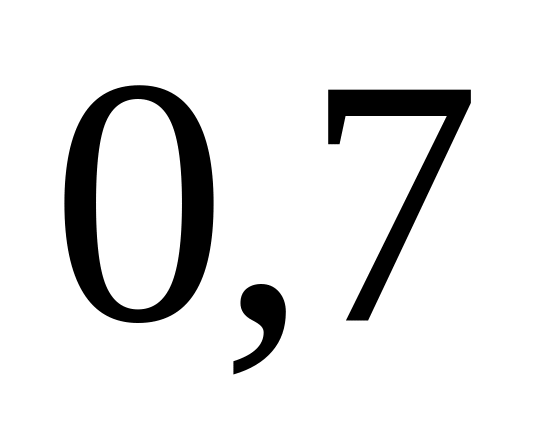 мм.
Случайная
величина
распределена
нормально с параметрами
мм.
Случайная
величина
распределена
нормально с параметрами
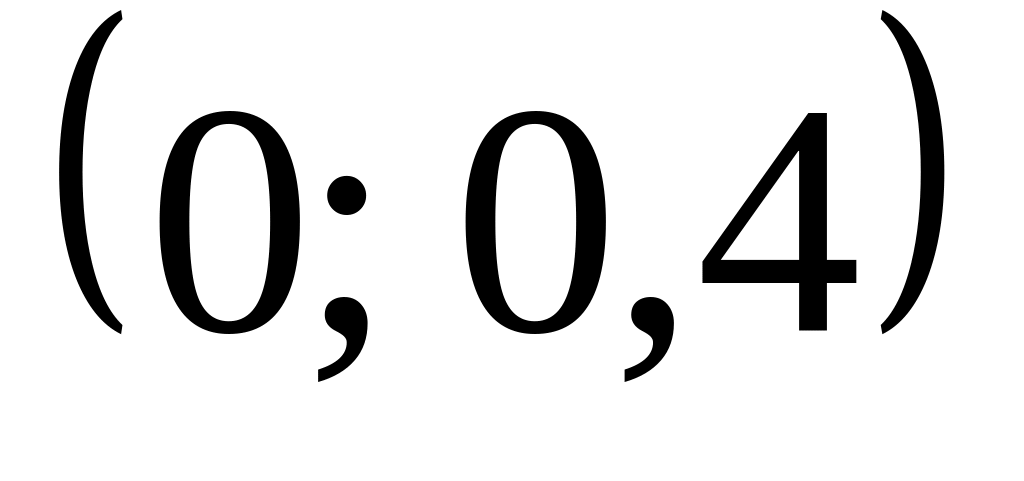 .
Найти вероятность того, что среди пяти
проверенных шариков все годные, если
измерения производились независимо.
.
Найти вероятность того, что среди пяти
проверенных шариков все годные, если
измерения производились независимо.
