17. Какая алгебраическая структура называется кольцом? Приведите пример кольца.

Если множество по сложению абелева группа, а по умножению – моноид, то это кольцо. (Целые числа)

18. Какая алгебраическая структура называется полем? Для поля Галуа gf(2) задайте с помощью таблиц бинарные операции сложения и умножения.

Если множество и по сложению и по умножению абелева группа, а также выполняется закон дистрибутивности: a(b+c)=ab+ac. (Вещественные числа).

+	0	1
0	0	1
1	1	0

*	0	1
0	0	0
1	0	1

19. Дайте определение метрического пространства. Перечислите аксиомы, которым должна удовлетворять метрика.

Множество Х элементов различной природы образует метрическое пространство, если любой паре элементов x_i, x_j, принадлежащих данному множеству (x_i, x_j Х), поставлено в соответствие (определено) неотрицательное вещественное число  (x_i, x_j), называемое расстоянием между элементами x_i и x_j.

Способ измерения расстояния должен удовлетворять:

1.  (x_i, x_j) = 0, только если x_i = x_j

2. Симметрия:  (x_i, x_j) =  (x_j, x_i).

3. Аксиома треугольника: x_i, x_j, x_k  Х (x_i, x_k)  (x_i, x_j) + (x_j, x_k)

20. Дайте определение метрического пространства. Приведите не менее двух примеров метрических пространств, указав используемые в них метрики.

Множество Х элементов различной природы образует метрическое пространство, если любой паре элементов x_i, x_j, принадлежащих данному множеству (x_i, x_j Х), поставлено в соответствие (определено) неотрицательное вещественное число  (x_i, x_j), называемое расстоянием между элементами x_i и x_j.

Примеры:

Множество действительных чисел R при задании расстояния как , где x и y – любые числа, принадлежащие R, образует метрическое пространство R.

Пусть для элементов множества Х  (x_i, x_j) = . - пространство изолированных точек.

Будем называть упорядоченную совокупность из n действительных чисел n-мерным вектором  = ( ). – векторное пространство. В нем бывают евклидова метрика: ; евклидова для комплексных чисел: ; метрика Хэмминга: ; метрика равномерного приближения:

21. Какие метрики обычно используются в пространствах Rn, c[a, b], l2[a, b]? Что это за пространства?

R_n – бесконечно мерное пространство (Евклидово), в нем используется евклидова метрика: , при

C [a, b] – пространство функций непрерывное на отрезке, в нем используется евклидова метрики:

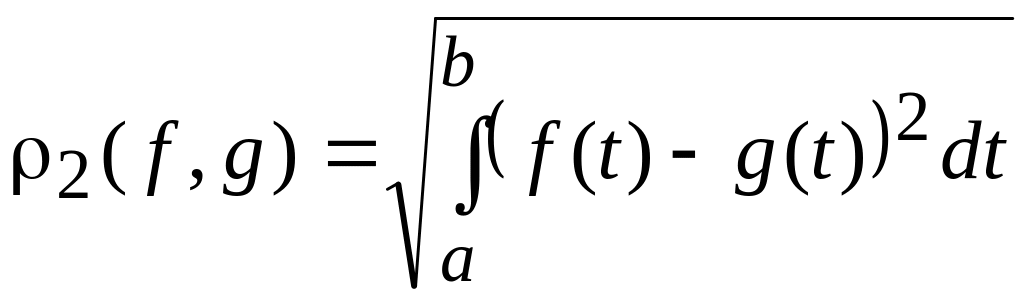
L2[a, b] – множество функций с интегрируемым квадратом ( ). Метрики те же самые.

22. Что называется нормой элемента произвольного векторного пространства? Каким условиям должен удовлетворять способ введения нормы?

Нормой элемента произвольного векторного пространства Х, обозначаемой как || ||, называют неотрицательное вещественное число. Способ введения нормы должен удовлетворять условиям:

1. || || = 0, только если = ;

2. || || = ||  || || , где  – скаляр;

3. || + ||  || || + || || (неравенство треугольника).