Все задания выполняються в Microsoft Excel В конце каждого задания находятся вопросы, на которые нужно уметь отвечать.

Минимум за две недели до зачета необходимо отправить электронный вид выполненого задания и отчета. 

Задание 1. Первичная обработка исходных данных

1. Собрать 360 данных за 1 календарный год по акциям ведущих компаний России. Данные записать в виде таблицы:

№ дня или t	дата	Цена открытия (y)
1	1 мая	32, 745
2	2 мая	32, 795
..........	............	............................................
360	30 июня	31, 195

2. По цене открытия построить гистограмму.

3. Провести первичную статистическую обработку данных. Использовать опции Данные →Анализ данных→Описательная статистика

4. Исследовать данные на однородность. Использовать коэффициент вариации

V_y = (σ_y/ ) 100%.

где - дисперсия (взять из таблицы описательная статистика), – среднее по цене открытия.

При этом следует ответить на вопрос: нужно ли разные порции данных обрабатывать разными способами?

5. Отсортировать данные и сгруппировать их в k = 3,22* ln(n) + 1 групп (число интервалов должно быть целое число!), где n-кол-во данных.

С помощью функции ЧАСТОТА определить количество данных, попавших в каждую группу. Для этого необходимо найти и размах .

Строим таблицу

Границы интервала	Частота (с помощью функции ЧАСТОТА)
…
…
…

Чтобы проверить правильность выполнения функции ЧАСТОТА, сумма в столбце Частота должна равняться кол-ву ваших данных.

Построить график частот. На этом графике показать моду, медиану, среднее значение, асимметрию, эксцесс.

6. По гистограмме построить 5 типов линий тренда. Выбрать из них наилучшую по R². И по экономическим соображениям( объяснить почему).

Контрольные вопросы.

1. Что такое среднее значение, мода, медиана, дисперсия? Их формулы и экономический смысл.

2. Что такое асимметрия, эксцесс, стандартная ошибка? Их формулы и экономический смысл.

3. Экономический смысл коэффициента вариации.

Задание 2. Построение и анализ линейной линии тренда

Построить линейное уравнение парной регрессии (линии тренда), заполнить все приведенные ниже таблицы и построить графики.

Ваше уравнение регрессии имеет вид: Y = a + b*t

1. Коэффициенты a, b определить с помощью Данные→Поиск решения из условия

∑(Y_t - a – b*t )² → min

В Excel это можно организовать с помощью функции Поиск Решений

(для подключения этого инструмента в программном продукте MS Office Exсel 2007 необходимо выполнить следующее:

1. Щелкните значок Кнопка Настройка панели быстрого доступа , а затем щелкните Другие команды.

2. Выберите команду Надстройки, а затем в окне Управление выберите пункт Надстройки Excel.

3. Нажмите кнопку Перейти.

4. В окне Доступные надстройки установите флажок Поиск решения и нажмите кнопку ОК.

Совет Если Поиск решения отсутствует в списке поля Доступные надстройки, чтобы найти надстройку, нажмите кнопку Обзор.

В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.

5. После загрузки надстройки для поиска решения в группе Анализ на вкладки Данные становится доступна команда Поиск решения.)

2. Заполнить все приведенные ниже 4 таблицы и построить 2 графика.

Для заполнения таблицы «Регрессионная статистика» (Таблица 1) находим:

1. Множественный R – r-коэффициент корреляции между у и t.

Для этого следует воспользоваться функцией КОРРЕЛ, введя массивы у и t.

Полученное в результате число показывает связь между опытными данными и расчетными.

2. Для расчета R-квадрат находим:

Объясняемая ошибка ,

.

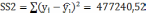Необъясняемая ошибка .

где

Следовательно, R-квадрат равен .

Соответственно 97% опытных данных объяснимы полученным уравнением регрессии.

3. Нормированный R-квадрат находим по формуле

n – количество наблюдений,

p – число степеней свободы (количество независимых переменных в уравнении регрессии)

Этот показатель служит для сравнения разных моделей регрессии при изменении состава объясняющих переменных.

4. Стандартная ошибка – квадратный корень из выборочной остаточной дисперсии:

.

В результате получаем следующую таблицу.

Таблица 1