
Тема 3. Банаховы пространства
Основные понятия: нормированное векторное пространство, последовательность Коши (фундаментальная последовательность), полнота пространства, эквивалентные нормы, ряды в банаховых пространствах, критерий банаховости.
Примеры решения задач
Задача №1. Доказать, что в пространстве C1[a, b] нормы
![]() ,
,
![]()
эквивалентны.
Решение.
Две нормы являются эквивалентными, если
они подчинены друг другу. Норма
![]() подчинена
подчинена
![]() ,
если сущeствует положительная константа
,
такая, что
,
если сущeствует положительная константа
,
такая, что
![]() .
.
![]()
![]() .
.
С другой стороны, используя формулу Ньютона-Лейбница для непрерывно-дифференцируемых функций
![]() ,
,
получим неравенство
![]() .
Проинтегрируем обе части по t:
.
Проинтегрируем обе части по t:
![]() или
или
![]() .
.
Таким образом,
![]()
![]()
![]()
 .
.
Задача № 2. Является ли пространство C1[0, 1] банаховым по норме
![]() .
.
Решение.
Нормальное векторное пространство
является банаховым, если любая
последовательность Коши в нем сходится.
По определению последовательность
является последовательностью Коши,
если
![]() при n, m
.
Имеем,
при n, m
.
Имеем,
![]() при n,
m
.
Значит,
при n,
m
.
Значит,
![]() и
и
![]() при n, m
одновременно.
при n, m
одновременно.
В силу полноты
пространства L[0,
1] последовательность
xn(t)
сходится в среднем к функции x0(t),
а последовательность непрерывных
функций
![]() сходится равномерно к непрерывной
функции (t).
Мы должны показать, что x0(t)
C1[0,
1] и
сходится равномерно к непрерывной
функции (t).
Мы должны показать, что x0(t)
C1[0,
1] и![]() .
Из сходимости в среднем следует, что
существует подпоследовательность
.
Из сходимости в среднем следует, что
существует подпоследовательность
![]() ,
сходящаяся к x0(t)
почти всюду. Пусть для t
= t0
и
,
сходящаяся к x0(t)
почти всюду. Пусть для t
= t0
и![]() при k
,
тогда
при k
,
тогда
 .
Перейдем к пределу при k
,
получим
.
Перейдем к пределу при k
,
получим
![]()
 почти всюду.
почти всюду.
Учитывая, что x0(t) абсолютно непрерывная функция, имеем .
Данная задача
может быть решена и следующим образом.
Известно, если в пространстве заданы
две эквивалентные нормы, по одной из
которых пространство банахово, то оно
банахово и по второй норме. В задаче №
1 мы показали, что наша норма эквивалентна
норме
![]() ,
по которой C1[0,
1] банахово. Значит C1[0,
1] банахово и по норме
,
по которой C1[0,
1] банахово. Значит C1[0,
1] банахово и по норме
![]() .
.
Задача №3.
Доказать, что пространство M[a,
b] - ограниченных
на отрезке [a,
b] функций с
нормой
![]() является банаховым.
является банаховым.
Решение:
Пусть xn
-
последовательность Коши в пространстве
M[a,
b]. Это значит,
что xn(t)
- ограниченные на отрезке [a,
b] функции и
![]() .
(*)
.
(*)
Зафиксируем t,
получим числовую последовательность
xn(t)
такую, что
![]() при n, m
.
Это означает, что xn(t)
является числовай последовательностью
Коши и сходится в силу полноты R.
Пусть
при n, m
.
Это означает, что xn(t)
является числовай последовательностью
Коши и сходится в силу полноты R.
Пусть
![]() .
Получили функцию x0(t),
к которой последовательность xn(t)
сходится точечно. Остается доказать,
что xn(t)
M[a,
b] и
.
Получили функцию x0(t),
к которой последовательность xn(t)
сходится точечно. Остается доказать,
что xn(t)
M[a,
b] и
![]() при n
.
Перейдем в равенстве (*) к пределу при
m
,
получим
при n
.
Перейдем в равенстве (*) к пределу при
m
,
получим
![]() .
.
Функция
![]() ограничена, значит и
ограничена, значит и
![]() ограничена, так как
ограничена, так как
![]() .
Таким образом, пространство M[a,
b] является
банаховым.
.
Таким образом, пространство M[a,
b] является
банаховым.
Задача № 4. Является ли последовательность

последовательностью Коши в пространстве L2 [-1, 1] ? Найти предел, если он существует.
Решение: По определению последовательность xn(t) является последовательностью Коши, если
 .
.
Поскольку интегралы
Лебега от эквивалентных функций
совпадают, заменим xn(t)
на yn(t)
такую, что xn(t)
yn(t),
где
![]() .
Имеем
.
Имеем
![]()
![]() при m
> n.
при m
> n.
Рассмотрим
последовательность
![]() ,
которая точечно сходится к нулю и
ограничена :
,
которая точечно сходится к нулю и
ограничена :![]() .
Воспользуемся теоремой Лебега о
предельном переходе под знаком интеграла
Лебега, получим
.
Воспользуемся теоремой Лебега о
предельном переходе под знаком интеграла
Лебега, получим
![]()
![]() .
.
Это означает, что
![]() ,
т.е. последовательность yn(t)
и, следовательно хn(t)
является последовательностью Коши и
сходится к функции t
L2
[-1,1].
,
т.е. последовательность yn(t)
и, следовательно хn(t)
является последовательностью Коши и
сходится к функции t
L2
[-1,1].
Задание №1.
Определите, являются ли две нормы
![]() и
и
![]() эквивалентными в нормированном
пространстве
эквивалентными в нормированном
пространстве
![]() два раза непрерывно-дифференцируемых
на отрезке
два раза непрерывно-дифференцируемых
на отрезке
![]() функций.
функций.
1.1.
![]() и
и
![]() ;
;
1.2.
и
![]() ;
;
1.3.
и
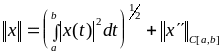 ;
;
1.4.
![]() и
и
![]() ;
;
1.5. и
 ;
;
1.6.
![]() и
и
;
Определите, являются
ли две нормы эквивалентными в нормированном
пространстве
![]() непрерывно-дифференцируемых на отрезке
[a,b] функций.
непрерывно-дифференцируемых на отрезке
[a,b] функций.
1.7.
![]() и
и
![]() ;
;
1.8.
и
![]() ;
;
1.9.
![]() и
и
![]() .
.
1.10. Доказать, что
в
![]() эквивалентна норме
эквивалентна норме
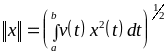 ,
где
,
где
![]() и v(t)
.
и v(t)
.
Доказать по
определению эквивалентность норм в
пространстве
![]()
1.11.
![]() и
и
![]() ;
;
1.12. .
![]() и
и
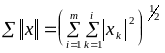 ;
;
1.13.
![]() и
и
![]() ;
;
1.14.
и
![]() ;
;
Задание №2.
Является ли последовательность
последовательностью Коши в пространстве
![]() .
Найти ее предел, если он существует.
.
Найти ее предел, если он существует.
2.1.
![]() ,
,
![]() ;
;
2.2.
![]() ,
,
![]() ;
;
2.3.
![]() ,
,
![]() ;
;
2.4.
![]() ,
,
![]() ;
;
2.5.
![]() ,
,
![]() ;
;
2.6.
![]() ,
,
![]() ;
;
2.7.
![]() ,
,
![]() ;
;
2.8.
![]() ,
,
![]() ;
;
2.9.
![]() ,
,
![]() ;
;
2.10.
![]() ,
,
![]() ;
;
2.11.
![]() ,
,
![]() ;
;
2.12.
![]() ,
;
,
;
2.13.
![]() ,
,
![]() ;
;
2.14.
![]() ,
.
,
.
Задание №3. Выяснить, является ли заданное пространство полным по указанной норме.
3.1. Пространство
![]() непрерывно-дифференцируемых
на отрезке [a,
b] функций с
нормой
непрерывно-дифференцируемых
на отрезке [a,
b] функций с
нормой
![]() ;
;
3.2. Пространство
с нормой
![]() ;
;
3.3. Пространство![]() с
нормой
с
нормой
![]() ;
;
3.4. Пространство
l2
числовых последовательностей
![]() ,
для которых выполняются следующие
соотношения:
,
для которых выполняются следующие
соотношения:
![]() с нормой
с нормой
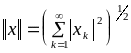 ;
;
3.5. Пространство
с нормой
![]() ;
;
3.6. Пространство
с нормой
![]() ;
;
3.7. Пространство
Rn
столбцов
![]() ,
,
![]() с нормой
с нормой
![]() ;
;
3.8. Пространство
Rn
столбцов
![]() ,
с нормой
,
с нормой
 ;
;
3.9. Пространство
![]() непрерывных функций с нормой
непрерывных функций с нормой
 ;
;
3.10. Пространство
с
нормой
![]() ;
;
3.11. Пространство
Rn
столбцов
![]() ,
с нормой
,
с нормой
 ;
;
3.12. Пространство Rn столбцов , с нормой
![]() ;
;
3.13. Пространство k непрерывных на R конечных функций (равных нулю за пределами некоторого промежутка, своего для каждой функции) с нормой
![]() ;
;
3.14. Пространство
![]()
![]() ,
,![]() с
нормой
с
нормой
![]() .
.
Задание
№4. Проверить,
сходится ли ряд
![]() в нормированном пространстве Е.
в нормированном пространстве Е.
4.1.![]()
4.2.
![]()
4.3.
![]()
4.4.
![]()
4.5.
![]()
4.6.
![]()
4.7.
![]()
4.8.
![]()
4.9.
![]()
4.10.

4.11.
![]()
4.12.

4.13.
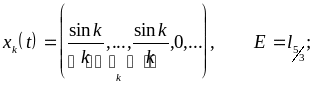
4.14.

