1.3. Задание системы в пространстве переменных состояний с помощью ss-объекта

Если известно описание системы в пространстве переменных состояний в виде матриц A, B, C и D, то задать эту систему в среде MATLAB можно с помощью функции ss:

sys=ss(A,B,C,D), где sys – любое выбираемое пользователем имя системы.

Пример.

Пусть система описана в пространстве переменных состояний с помощью матриц , , , .

Тогда для задания этой системы в среде MATLAB необходимо записать следующие строчки:

>> A=[0 1;-5 -2];

>> B=[0;3];

>> C=[0 1];

>> D=0;

>> sys=ss(A,B,C,D)

a =

x1 x2

x1 0 1

x2 -5 -2

b =

u1

x1 0

x2 3

c =

x1 x2

y1 0 1

d =

u1

y1 0

2. Функции реализации параллельного, последовательного и соединения с обратной связью

2.1. Параллельное соединение

Функция sys=parallel(sys1,sys2) реализует параллельное соединение двух систем. Эта функция эквивалентна операции сложения sys=sys1+sys2.

2.2. Последовательное соединение

Функция sys=series(sys1,sys2) реализует последовательное соединение двух систем. Эта функция эквивалентна операции умножения систем sys=sys1*sys2.

2.3. Соединение с обратной связью

Функция sys=feedback(sys1,sys2) возвращает систему sys, соответствующую соединению систем sys1 и sys2 в контур с отрицательной обратной связью. Причем система sys1 находится в прямой передаче, а система sys2 – в обратной связи.

Чтобы замкнуть систему положительной обратной связью, следует использовать следующее обращение: sys=feedback(sys1,sys2,+1).

Внимание! Очень частой ошибкой бывает использование следующей записи при построении соединения с обратной связью: . В данном случае операция замыкания контура обратной связью в среде MATLAB будет выполнена некорректно. Поэтому для реализации соединения с обратной связью необходимо использовать функцию feedback.

3. Анализ динамических систем в среде matlab

3.1. Вычисление нулей и полюсов системы

Функция p=pole(sys) возвращает вектор p, состоящий из полюсов системы sys.

Функция z=tzero(sys) возвращает вектор z, состоящий из нулей передаточной функции системы sys.

3.2. Вычисление и отображение полюсов и нулей системы на комплексной плоскости.

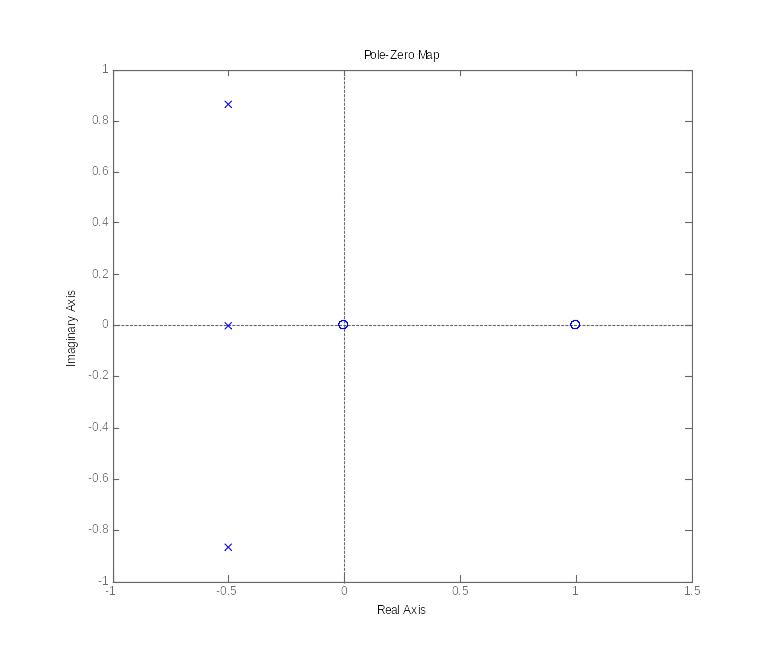
Для отображения полюсов и нулей системы на комплексной плоскости следует использовать функцию pzmap(sys).

Пример.

Пусть дана система в виде передаточной функции W:

Transfer function:

s^2 - s

-----------------------

2 s^3 + 3 s^2 + 3 s + 1

Тогда, воспользовавшись записью pzmap(W), получим следующий результат:

3.3. Построение логарифмических частотных характеристик

Функция bode(sys) предназначена для построения амплитудных и фазовых логарифмических частотных характеристик для динамических систем.

Пример.

Пусть требуется построить ЛАФЧХ для колебательного звена .

Обращение bode(W) позволит получить график ЛАФЧХ:

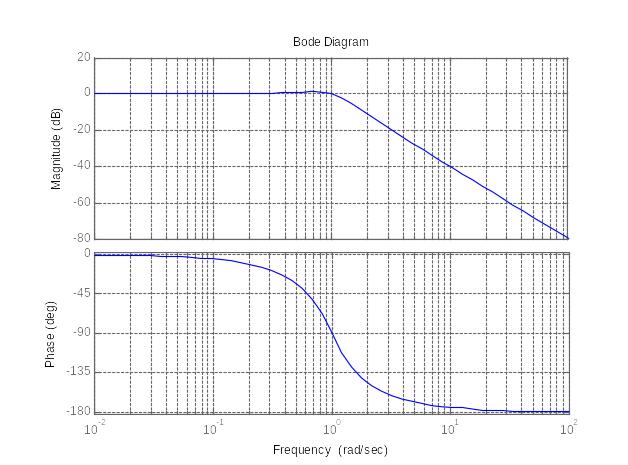
Примечание. Сетку на полученный график можно нанести с помощью команды grid on.

3.4. Построение годографа передаточной функции системы

Функция nyquist(sys) предназначена для построения частотного годографа передаточной функции динамической системы.

Пример. Пусть требуется построить годограф для колебательного звена из предыдущего примера.

Обращение nyquist(W) позволит получить годограф:

Примечание. По умолчанию система MATLAB строит годограф для полного диапазона частот от до . Часть годографа, соответствующую отрицательным частотам легко убрать. Для этого необходимо щелкнуть правой кнопкой мыши в области годографа, выбрать пункт меню Show и снять галочку с “Negative Frequencies”.

С помощью ЛАФЧХ и годографа возможно исследовать запасы устойчивости системы. Рассмотрим на следующем примере. Пусть дана система в разомкнутом состоянии .

Годограф этой системы будет иметь вид (для положительного диапазона частот):

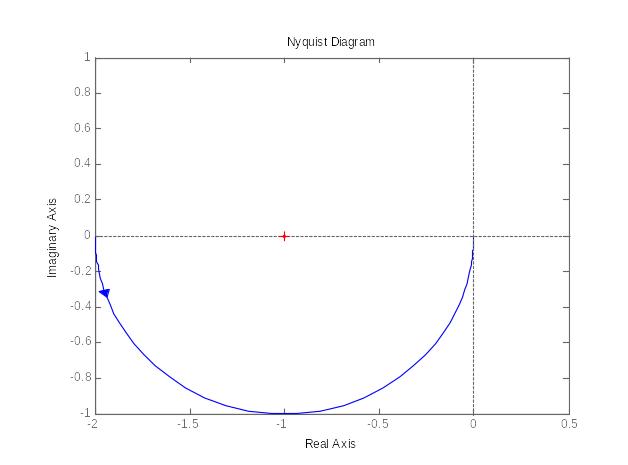
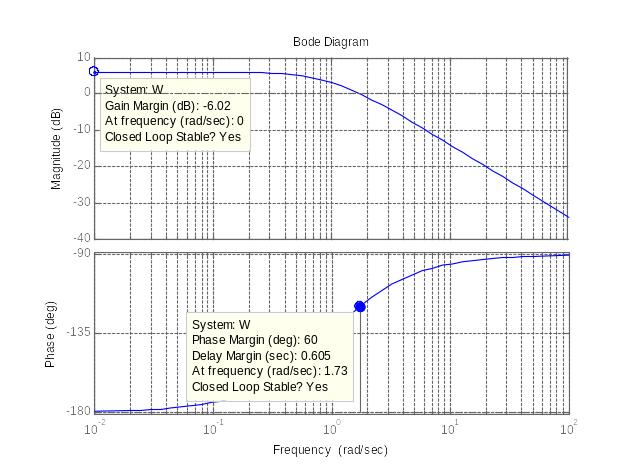
Щелкнув правой кнопкой мыши в области рисунка и выбрав пункт меню Characteristics->All Stability Margins, сможем увидеть запасы устойчивости по модулю и фазе:

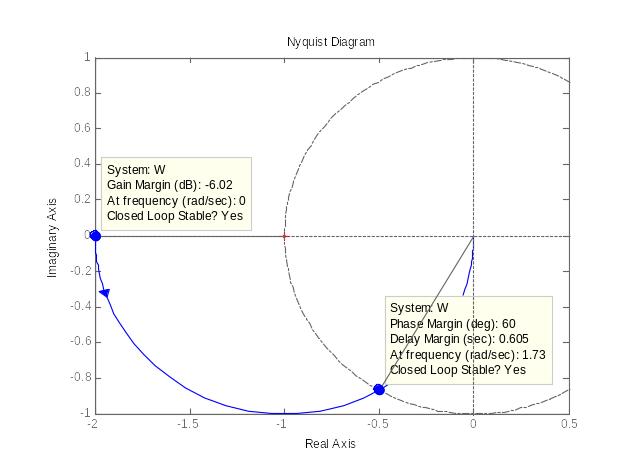
Примечание. Таким же образом запасы устойчивости можно увидеть и на ЛАФЧХ:

3.5. Построение переходной характеристики системы

Для построения переходной характеристики динамической системы предназначена функция step(W).

Пример.

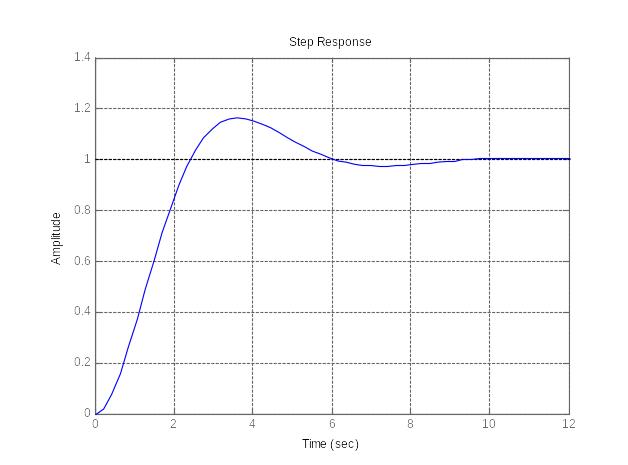
Пусть дана система в виде колебательного звена .

Тогда переходной процесс можно построить с помощью обращения step(W):

3.6. Построение импульсной переходной характеристики

Для построения импульсной переходной характеристики динамической системы предназначена функция impulse(W).

Примечание. Если дана система в разомкнутом состоянии, а требуется построить переходную или импульсную характеристику для замкнутой системы, то прежде чем использовать функцию step, сначала необходимо получить замкнутую систему с помощью функции feedback.

3.7. Построение корневого годографа (функция rltool)

При построении корневого годографа следует четко понимать, что исходными данными является разомкнутая система. А результатом построения корневого годографа является набор траекторий движения полюсов замкнутой системы при изменении коэффициента усиления разомкнутой системы от нуля до бесконечности.

Рассмотрим построение корневого годографа на примере.

Пусть дана разомкнутая система .

Расположение нулей и полюсов этой системы показано на рисунке:

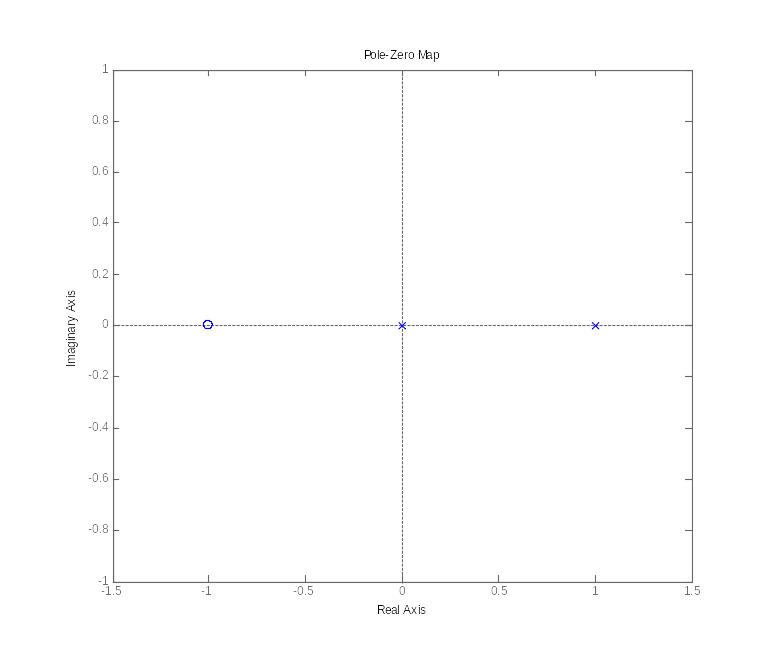
Задавать передаточную функцию разомкнутой системы следует для K=1 (истинный коэффициент усиления равен 1):

Сформируем заданную передаточную функцию, например, с помощью функции tf:

>> W=tf([1 1],[1 -1 0])

Transfer function:

s + 1

-------

s^2 – s

Корневой годограф можно построить с помощью обращения rltool(W):

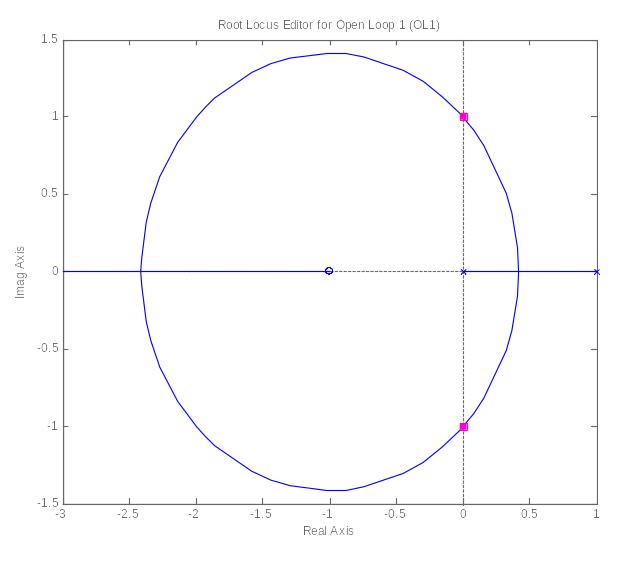
Квадратики, закрашенные красным цветом, показывают расположение полюсов замкнутой системы при том или ином значении коэффициента усиления разомкнутой системы. С помощью мыши можно перемещать эти полюса и следить за тем, как именно изменяется их расположение при изменении коэффициента усиления.

Примечение. Инструмент rltool позволяет в онлайн режиме добавлять нули и полюса в систему и следить за тем, как при этом изменится вид корневого годографа. Кроме того, в рамках этого инструмента есть возможность исследовать частотные и временные характеристики замкнутой системы.