
- •Лекция №1. Задачи начертательной геометрии. Методы проецирования. Комплексный чертеж точки.
- •1.1. Основные задачи начертательной геометрии (нг)
- •1.2. Методы проецирования
- •1.3. Проецирование точки на две взаимно - перпендикулярные плоскости. Образование комплексного чертежа (эпюр Монжа)
- •1.4. Проецирование точки на три взаимно- перпендикулярные плоскости. Законы проекционной связи.
- •1.5.Алгоритм построения комплексного чертежа точки по заданным координатам на три плоскости проекций
- •Лекция №2. Комплексный чертеж прямой линии
- •2.1. Определение и задание прямой линии в пространстве и на комплексном чертеже
- •2.2. Положение прямой относительно плоскостей проекций
- •Прямая общего положения.
- •Прямые уровня.
- •Проецирующие прямые
- •2.3. Определение натуральной величины отрезка прямой общего положения и углов наклона его к плоскостям проекций
- •2.5. Проекции плоских углов
- •2.5. Взаимное положение точки и прямой.
- •2.6. Взаимное расположение двух прямых в пространстве
2.5. Проекции плоских углов
Любой линейный угол проецируется на плоскость проекций в натуральную величину, если его стороны параллельны этой плоскости.
Рис. 2.14 |
Рис. 2.15 |
Прямые
|
Прямые
|
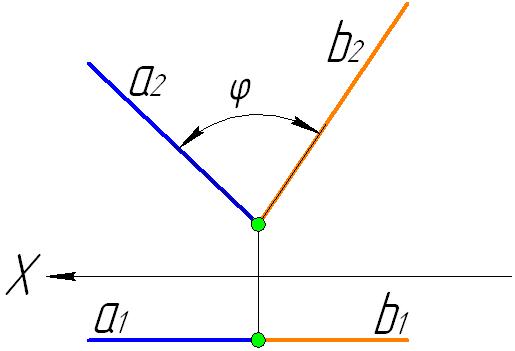
Прямой угол проецируется на плоскость в натуральную величину, если хотя бы одна из его сторон параллельна плоскости проекций, а другая является прямой общего положения.
|
|
Проекции прямого угла, одна сторона которого является фронталью
|
Проекции прямого угла, одна сторона которого является горизонталью
|
Рис. 2.16 |
Рис. 2.17 |
2.5. Взаимное положение точки и прямой.
Точка относительно прямой может занимать два положения: принадлежать этой прямой или находиться за ее пределами.
Если точка принадлежит прямой линии, то ее проекции лежат на одноименных проекциях этой прямой и на общей линии проекционной связи.
На рис.2.18
изображенная точка
,
которая принадлежит прямой
,
так как ее проекции
и
расположены соответственно на
горизонтальной
Если точка не принадлежит прямой линии, то возможные два варианта: 1)
ни одна из
проекций точки, например, точка
|
Рис. 2.18 |
2)
одна из проекций точки принадлежит
одноименной проекции прямой линии, а
вторая нет:
 .
.
Деление отрезка прямой в заданном отношении
Если точка делит прямую в некотором отношении, то проекции точки делят проекции прямой в том же отношении.
На рис. 2.19 показано
построение деления отрезка
точкой
Построение: (построение можно начинать с любой плоскости проекций П1,П2 или П3, а также с любой точки: или ): |
Рис. 2.19 |
1. из фронтальной
проекции точки
 произвольно проводим луч под любым
углом;
произвольно проводим луч под любым
углом;
2. отрезок
нужно разделить в отношении
 ,
следовательно, должно быть пять одинаковых
частей. На произвольном луче откладываем
пять произвольных, но равных между собой
отрезков. Получаем точку
’.
,
следовательно, должно быть пять одинаковых
частей. На произвольном луче откладываем
пять произвольных, но равных между собой
отрезков. Получаем точку
’.
3. соединяем точку
’
с фронтальной проекцией точки
 .
.
4. отрезок
 ’
имеет пять одинаковых частей. Обозначаем
на нем точку
’
имеет пять одинаковых частей. Обозначаем
на нем точку
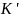 (три части от фронтальной проекции точки
);
(три части от фронтальной проекции точки
);
5. из точки
проводим линию
 - получаем фронтальную проекцию точки
- получаем фронтальную проекцию точки
 ;
;
6. в соответствии
с первым законом проекционной связи
определяем горизонтальную проекцию
точку
 ;
;
7. после выполненных
действий получаем:
 ,
,
 .
.


 и
- прямые фронтального уровня, поэтому
на фронтальную плоскость проекций П2
проецируются в натуральную величину.
Следовательно угол
и
- прямые фронтального уровня, поэтому
на фронтальную плоскость проекций П2
проецируются в натуральную величину.
Следовательно угол
 - угол между прямыми
и
проецируется в натуральную величину
на фронтальную плоскость проекций
П2.
- угол между прямыми
и
проецируется в натуральную величину
на фронтальную плоскость проекций
П2. и
и
 - прямые горизонтального уровня,
поэтому на горизонтальную плоскость
проекций П1
проецируются в натуральную величину.
Следовательно угол
- прямые горизонтального уровня,
поэтому на горизонтальную плоскость
проекций П1
проецируются в натуральную величину.
Следовательно угол
 между прямыми
и
проецируется в натуральную величину
на горизонтальную плоскость проекций
П1.
между прямыми
и
проецируется в натуральную величину
на горизонтальную плоскость проекций
П1.


 и фронтальной
и фронтальной
 проекциях прямой.
проекциях прямой. не принадлежит соответствующей
проекции прямой;
не принадлежит соответствующей
проекции прямой;

 в отношении
в отношении
 .
.