Проецирующие прямые

Проецирующие прямые – прямые, перпендикулярные к какой либо плоскости проекций.

Проецирующие прямые одновременно параллельные двум плоскостям проекций и потому, как следствие, они перпендикулярные третий.

Проецирующая прямая проецируется в точку на ту плоскость проекций, которой она перпендикулярна, а на две другие плоскости проекций - в натуральную величину, т к. она им параллельна.

Горизонтально проецирующая прямая	Фронтально проецирующая прямая	Профильно проецирующая прямая

Рис. 2.11. Проецирующие прямые

2.3. Определение натуральной величины отрезка прямой общего положения и углов наклона его к плоскостям проекций

Как видим с изложенного, для прямой частного положения не возникает проблем при определении на комплексном чертеже натуральной величины ее отрезка и углов наклона к плоскостям проекций. Но на практике часто возникает необходимость определить натуральную величину отрезка прямой общего положения и натуральную величину углов, которые она составляет с плоскостями проекций.

Рассмотрим рис.2.12, из которого вытекает так называемое правило прямоугольного треугольника, которое поможет решить эту проблему.

Возьмем на прямой произвольные точки , определяющие отрезок [ ], и построим их соответствующие проекции , ; , . Через точку проведем прямую , параллельную , а через точку - прямую , параллельную .

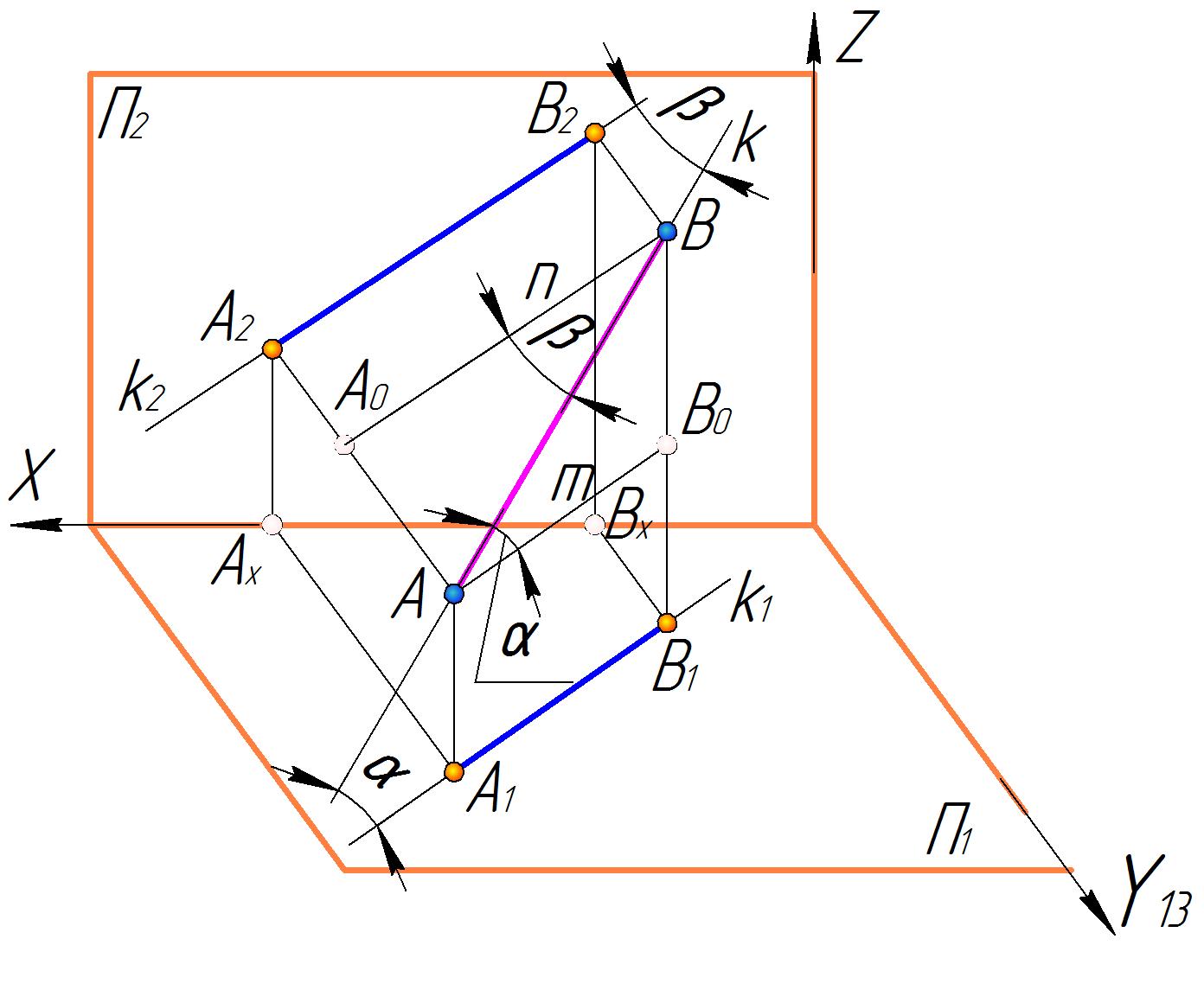
Рис. 2.12.

Получим два прямоугольных треугольника и , у которых: [ ] - гипотенуза (отрезок [ ] - натуральная величина), - угол наклона прямой к горизонтальной плоскости проекций П₁, - угол наклона прямой к фронтальной плоскости проекций П₂.

Для треугольника катет [ ] равняется величине горизонтальной проекции [ ] отрезка [ , т.е. [ ] = [ ]; второй катет [ ] равняется разности расстояний от концов отрезка (точки и ) к горизонтальной плоскости проекций, т.е. [ ] - [ ] = [ ] .

Аналогичные выводы также вытекают из рассмотрения треугольника относительно угла наклона прямой к фронтальной плоскости проекций, что дает основание сформулировать общее правило прямоугольного треугольника.

Для определения натуральной величины угла наклона прямой к плоскости проекций и натуральной величины отрезка этой прямой нужно на комплексном чертеже (рис.2.13) построить прямоугольный треугольник, у которого один (базовый) катет есть проекция отрезка [ ] на ту плоскость проекций, относительно которой определяется угол наклона прямой, а второй - алгебраическая разность расстояний от концов отрезка к той же плоскости проекций ( недостаточной координаты).

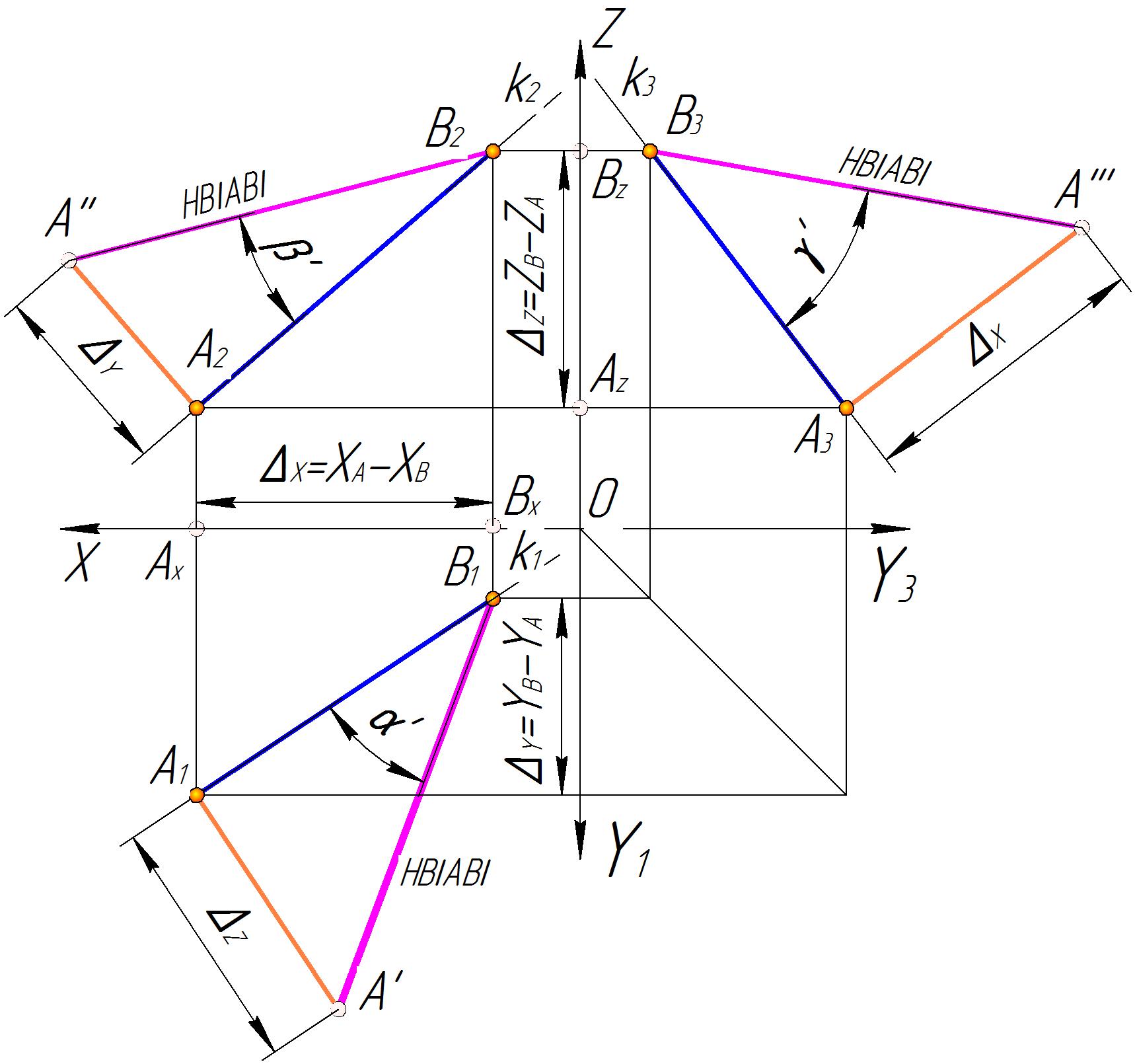
Рис. 2.13. Определение натуральной величины отрезка прямой линии общего положения

Тогда гипотенуза такого треугольника будет равняться натуральной величине отрезка [ ] прямой , а угол между соответствующей проекцией этого отрезка и его натуральной величиной равняться натуральной величине угла наклона прямой к этой плоскости проекций.

Итак, для построения угла 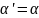за базовый катет нужно принять горизонтальную проекцию [ ] отрезка [ ], второй катет будет равняться отрезку (рис.2.13); для - фронтальную проекцию ], второй катет - ; для - профильную проекцию ], второй катет - .