
- •Лекция №1. Задачи начертательной геометрии. Методы проецирования. Комплексный чертеж точки.
- •1.1. Основные задачи начертательной геометрии (нг)
- •1.2. Методы проецирования
- •1.3. Проецирование точки на две взаимно - перпендикулярные плоскости. Образование комплексного чертежа (эпюр Монжа)
- •1.4. Проецирование точки на три взаимно- перпендикулярные плоскости. Законы проекционной связи.
- •1.5.Алгоритм построения комплексного чертежа точки по заданным координатам на три плоскости проекций
- •Лекция №2. Комплексный чертеж прямой линии
- •2.1. Определение и задание прямой линии в пространстве и на комплексном чертеже
- •2.2. Положение прямой относительно плоскостей проекций
- •Прямая общего положения.
- •Прямые уровня.
- •Проецирующие прямые
- •2.3. Определение натуральной величины отрезка прямой общего положения и углов наклона его к плоскостям проекций
- •2.5. Проекции плоских углов
- •2.5. Взаимное положение точки и прямой.
- •2.6. Взаимное расположение двух прямых в пространстве
1.5.Алгоритм построения комплексного чертежа точки по заданным координатам на три плоскости проекций
Алгоритмом называется ряд последовательных действий, которые необходимо выполнить.
Для решения определенной задачи необходимо иметь координаты точки. Алгоритм построения проекций точки (рис.1.20) по координатам ( ) заключается в следующем:
1. Построение горизонтальной проекции точки
|
1.1. На оси
откладываем значение координаты
1.2.
на оси
1.3. из полученных точек и проводим линии проекционной связи перпендикулярно осям и до их пересечения; 1.4. в результате выполненных действий получим горизонтальную проекцию точки → . |
2. Построение фронтальной проекции точки
|
2.1. На оси откладываем значение координаты , получаем ; 2.2.
на оси
откладываем значение координаты
2.3. из полученных точек и проводим линии проекционной связи перпендикулярно осям и до их пересечения; 2.4. в результате выполненных действий получим фронтальную проекцию точки → . |
3. Построение профильной проекции точки
|
3.1. На оси откладываем значение координаты , получаем ; 3.2.
на оси
3.3. из полученных точек и проводим линии проекционной связи перпендикулярно осям и до их пересечения; 3.4. в результате выполненных действий получим профильную проекцию точки → . |
где – координаты точки в пространстве.
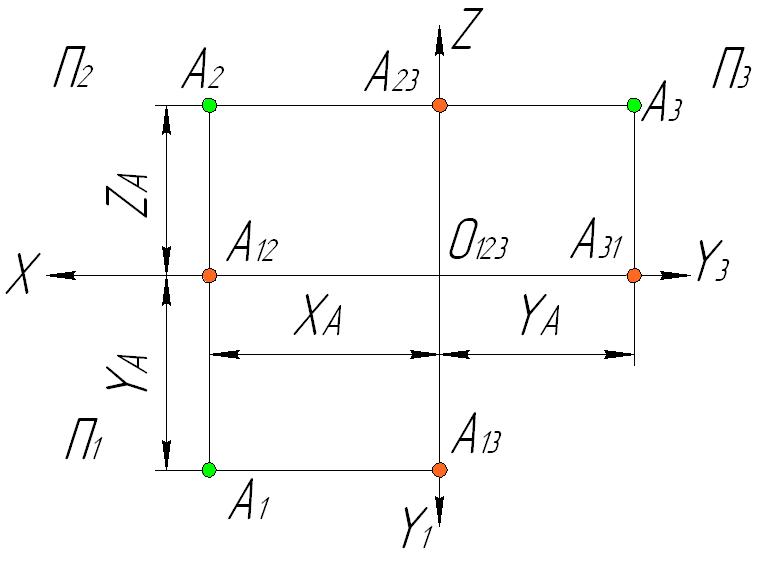
Рис.1.20
Лекция №2. Комплексный чертеж прямой линии
План
2.1. Определение и задание прямой линии в пространстве и на комплексном чертеже.
2.2. Положение прямой относительно плоскостей проекций.
2.3. Определение натуральной величины отрезка прямой общего положения и углов ее наклона к плоскостям проекций.
2.4. Проекции плоских углов.
2.5. Взаимное положение точки и прямой. Деление отрезка прямой в заданном отношении.
2.6. Взаимное положение двух прямых в пространстве.
2.8. Следы прямой линии.
2.1. Определение и задание прямой линии в пространстве и на комплексном чертеже
В общем случае прямая – это траектория некоторой точки, которая в процессе движения не изменяет своего направления.
Чтобы
задать прямую линию в пространстве,
необходимо задать совокупность таких
условий, которые бы определяли ее
однозначно. Исходя из этого, одну и ту
же прямую линию можно определить разными
элементами. Так, на рис.2.1а) прямая линия
определяется двумя точками
и
;
на рис. 2.1 б) - точкой
и направлением
;
на рис.2.1, в) - как результат пересечения
двух плоскостей ( ).
Но любой случай можно представить как
прямую, которая проходит через две
точки. Поэтому считается, что определителем
прямой являются две точки,
следовательно, на комплексном
чертеже прямая линия
будет определяться
соответствующими проекциями этих
элементов.
).
Но любой случай можно представить как
прямую, которая проходит через две
точки. Поэтому считается, что определителем
прямой являются две точки,
следовательно, на комплексном
чертеже прямая линия
будет определяться
соответствующими проекциями этих
элементов.

а) |
б) |
в) |
Рис. 2.1.
Рис. 2.2. |
Так, проведя,
например, через две точки пространства
и
(рис.2.2) прямые
и
перпендикулярные к плоскости проекций
П1,
получим проекции точек
и
|
Если
провести прямые, перпендикулярные к
плоскости П1
из двух других произвольных точек прямой
,
то так же получим проекцию прямой
.
Совокупность каждой из пар таких
перпендикулярных прямых образует
плоскость
 ,
которая перпендикулярная к плоскости
П1
и пересекается с ней по прямой
,
что подтверждает полученный результат.
,
которая перпендикулярная к плоскости
П1
и пересекается с ней по прямой
,
что подтверждает полученный результат.
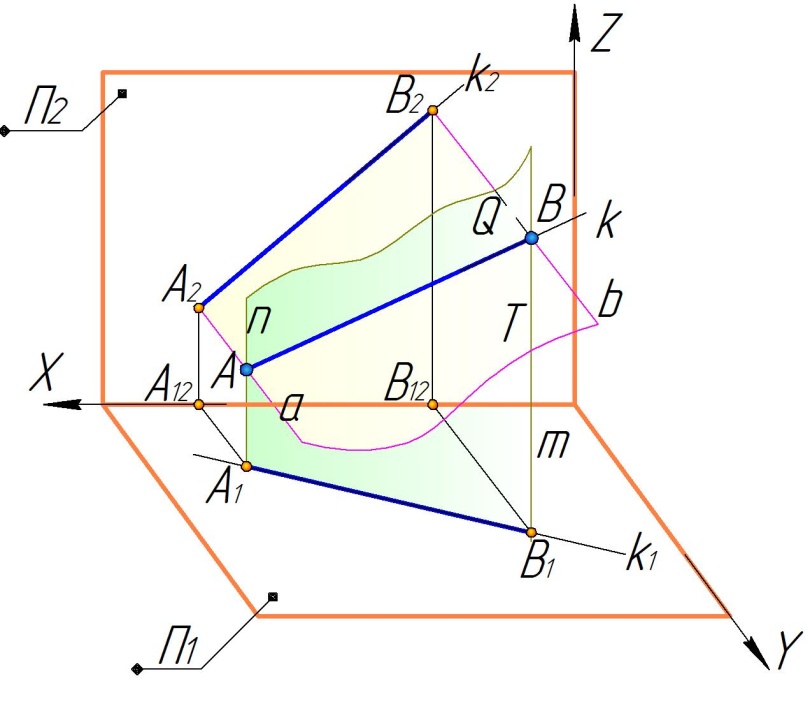
Рассматривая
аналогично процесс проецирования на
две взаимно перпендикулярные плоскости
проекций П1
и П2
получим соответственно горизонтальную
и фронтальную
 проекции прямой
(рис. 2.3).
проекции прямой
(рис. 2.3).
Нетрудно
заметить (рис. 2.2), что одна
проекция прямой не определяет ее
положения в пространстве.
Так, отрезок [ ]
может быть проекцией любого отрезка
[
]
может быть проекцией любого отрезка
[ ]
прямой
]
прямой
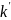 или отрезка [
или отрезка [ ]
прямой
]
прямой
 ,
расположенных в плоскости
.
Положение прямой в пространстве
определяется совокупностью, по крайней
мере, двух ее проекций. Итак, зная
положение горизонтальной
,
расположенных в плоскости
.
Положение прямой в пространстве
определяется совокупностью, по крайней
мере, двух ее проекций. Итак, зная
положение горизонтальной
 и фронтальной
и фронтальной
 проекций точек
и
прямой
(рис. 2.3), можно получить саму прямую
как результат пересечения плоскостей
и
проекций точек
и
прямой
(рис. 2.3), можно получить саму прямую
как результат пересечения плоскостей
и
 ,
которые получились соответственно из
проецирующих лучей
,
и
,
которые получились соответственно из
проецирующих лучей
,
и
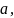
 .
.
|
Удаляя все
пространственные построения на рис.2.3
и оставляя только то, что получено на
плоскостях проекциях, получим
комплексный чертеж прямой
Напомним полученные названия проекций:
Построение третьей проекции выполненная с помощью второго и третьего законов |
Рис. 2.3. |
|
|
|
Рис. 2.4. |
проекционной связи относительно точек и .
Основные свойства прямой линии выражаются следующими аксиомами:
1. Через две точки пространства можно провести прямую и притом только одну.
2. Две прямые пересекаются только в одной точке.
3. Прямую линию можно продолжить в обе стороны.
Прямая
линия обозначается
 …;
проекции обозначаются -
…;
проекции обозначаются -
 …
…


 ,
получаем
;
,
получаем
; откладываем значение координаты
откладываем значение координаты
 ,
получаем
,
получаем
 ;
;
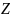 ,
получаем
,
получаем
 ;
;
 откладываем значение координаты
,
получаем
откладываем значение координаты
,
получаем
 ;
;
 ,
как результат пересечения этих
перпендикуляров с плоскостью П1.
Прямая
,
как результат пересечения этих
перпендикуляров с плоскостью П1.
Прямая
 ,
которая проходит через точки
и
- является соответствующей проекцией
прямой
.
,
которая проходит через точки
и
- является соответствующей проекцией
прямой
.
 ,
при этом совмещая в одну плоскость П1
и П2
(рис.2.4).
,
при этом совмещая в одну плоскость П1
и П2
(рис.2.4). - горизонтальная
проекция прямой
(отрезка [
]);
- горизонтальная
проекция прямой
(отрезка [
]); - фронтальная
проекция прямой
(отрезка [
]);
- фронтальная
проекция прямой
(отрезка [
]); - профильная
проекция прямой
(отрезка [
]).
- профильная
проекция прямой
(отрезка [
]).