1.3. Проецирование точки на две взаимно - перпендикулярные плоскости. Образование комплексного чертежа (эпюр Монжа)

Как видим из изложенного материала, метод проекций дает возможность полностью строить изображение. Согласно этому методу каждой точке трехмерного пространства относится в соответствие определенная точка двумерного пространства (плоскости). Поэтому в начертательной геометрии постоянно и почти параллельно решаются две основных задачи (прямая и обратная). Прямая задача заключается в том, что по оригиналу по определенным правилам строят его изображение.

Обратная задача решает другую проблему- по заданному изображению

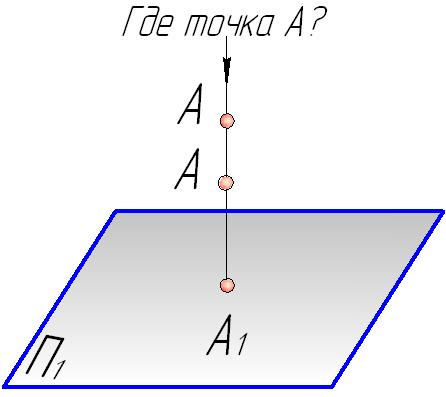
восстановить форму, положение оригинала в пространстве, а также решить определенную задачу метрического или позиционного характера. Но обратную задачу по одной проекции решить невозможно, так как одна проекция точки не определяет ее положения в пространстве, и чертеж является необратимым (рис.1.8).

Рис.1.8.

Для получения обратимого чертежа объект проецируют на две и три взаимно перпендикулярные плоскости проекций.

Рис.1.9. Гаспар Монж

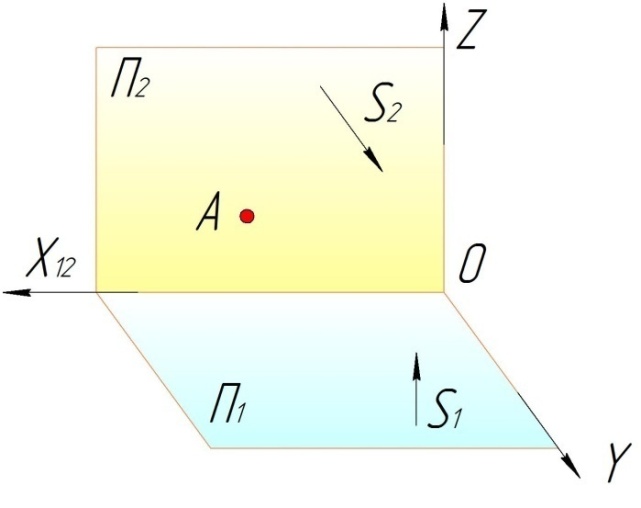
Французский ученый Гаспар Монж (1746-1818) предложил плоскости проекций П1 и П2 располагать между собой под прямым углом и строить изображение по методу параллельного ортогонального проецирования. Исходя из этого, модель Монжа (рис.1.10) предусматривает такой аппарат проецирования: имеются две взаимно - перпендикулярные плоскости

проекций, а проецирующие лучи должны проводиться перпендикулярно к соответствующим плоскостям проекций. Согласно этому через точку проведем проецирующие лучи: и (рис.1.11).

Рис.1.10

Рис.1.11

В результате образуется плоскость , которая однозначно перпендикулярна и к плоскости П₁ и к П₂ – следовательно она всегда пересекает их по прямым линиям: 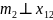и (рис.1.11). Отсюда является точкой пересечения проецирующего луча с плоскостью проекций П₁ и соответственно - луча с плоскостью П₂. Тогда, согласно определению, сделанному раньше, точки и 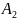являются соответствующими проекциями точки , и обозначения на рис.1.11 будут называться:

П₁ - горизонтальная плоскость проекций;

П₂ - фронтальная плоскость проекций;

- ось проекций (пересечение П₁ с П₂);

– точка, объект проецирования;

– проецирующие лучи;

- горизонтальная проекция точки ;

- фронтальная проекция точки ;

- осевая проекция точки ;

- линия проекционной связи.

Пространственная модель проецирования на две взаимно перпендикулярные плоскости, которая представлена на рис.1.11 очень неудобна для использования ее на практике, при выполнении исследований, а также на производстве, поэтому ее приводят к плоскому виду. Для этого после окончания процесса проецирования и, следовательно, получения соответствующих проекций надо точку , проецирующие лучи и , а также плоскость условно изъять, оставив только то, что получилось на плоскостях проекций при проецировании. В результате получим модель, представленную на рис.1.12 а). Дальше, вращая горизонтальную плоскость проекций П₁ вместе со всеми полученными на ней изображениями вокруг оси проекций (как это показано стрелочкой ) к полному совпадению ее с фронтальной плоскостью проекций П₂, получим изображение точки на совмещенных плоскостях проекций (рис.1.12 б). Такая плоская модель называется комплексный чертеж точки (или эпюр Монжа). Поскольку плоскости проекций имеют бесконечные размеры, становится нецелесообразным создавать «рамочку». Более того, обозначение плоскостей проекций П₁ и П₂ также можно изъять. В результате получим комплексный чертеж точки в конечном виде (рис.1.12 в).

а) б) в)

Рис.1.12.

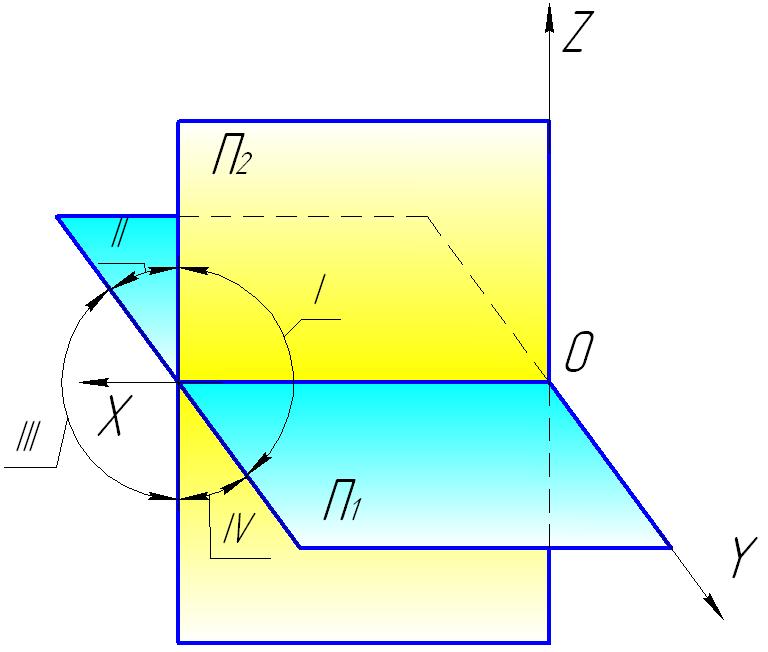
Рассматривая плоскости проекций П1 и П2 безграничными во все стороны, можно заметить (рис.1.13), что все пространство разделено на четыре части, каждая из которых имеет название четверть. Их нумерация показана на рис.1.13.

Рис.1.13.

Очевидно, что в зависимости от того, в какой четверти расположена точка, проекции ее также будут определенным образом расположены относительно оси проекций . В случае ее расположения в первой четверти (рис.1.11) фронтальная проекция должна быть только выше оси - луч будет пересекать фронтальную плоскость проекций П₂ всегда выше оси пока точка не совпадет с , т.е. это есть рубеж перехода от верхних четвертей (І, ІІ) к нижним (ІІІ, ІV). Рассмотрим горизонтальную проекцию : она должна быть расположена ниже оси , поскольку передняя пола горизонтальной плоскости проекций П₁, по принятому направлению совмещения, занимает именно это место. Если точка расположена во второй четверти, то ее фронтальная проекция будет выше оси (верхняя четверть). Горизонтальная проекция может быть только на заднем поле горизонтальной плоскости проекций П₁. При этом заднее поле горизонтальной плоскости проекций П₁ при принятом направлении движения (рис.1.12 а) займет положение над осью . Поэтому комплексный чертеж точки будет иметь в этом случае вид, представленный на рис.1.14 а

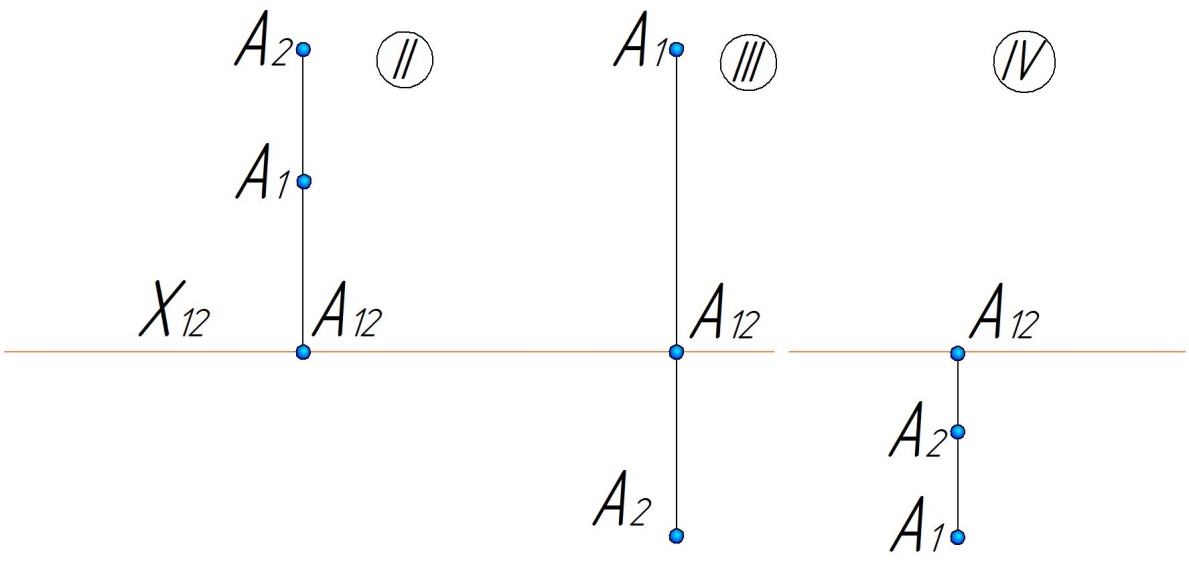
а) б) в)

Рис.1.14.

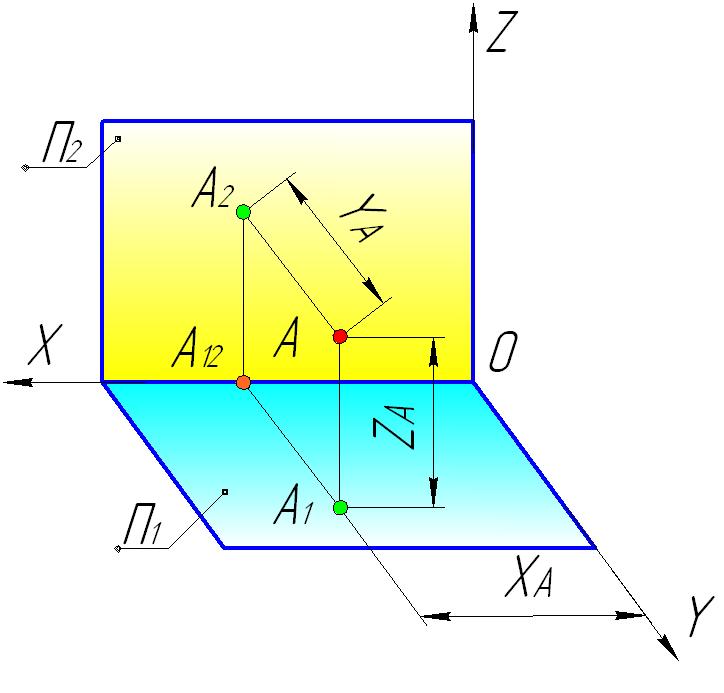
Последнее приводит к выводу, который для точки, в которой бы четверти она не была расположена, выполняется условие: на комплексном чертеже расстояние от горизонтальной проекции точки до оси всегда равняется в пространстве расстоянию от самой точки до фронтальной плоскости проекций П2, а расстояние от фронтальной проекции точки

Рис.1.15

до оси всегда равняется в пространстве расстоянию от самой точки до горизонтальной плоскости проекций П₁.

Отметим также, что горизонтальная и фронтальная проекции точки всегда находятся на одной прямой линии, перпендикулярной к оси , которая имеет название линия проекционной связи.

Установленные закономерности и сделанные выводы указывают на то, что комплексный чертеже в двух проекциях метрически определен, и позволяет восстановить форму, размеры оригинала и его положение в пространстве. Вытекает и механизм решения обратной задачи. Он заключается в том, что, во-первых, необходимо мысленно вернуть горизонтальную плоскость проекций П₁ в исходное положение, т.е. расположить ее перпендикулярно к фронтальной плоскости проекций П₂, как это изображено на рис.1.12 а. Во-вторых, через горизонтальную проекцию точки провести прямую линию , а через фронтальную проекцию - провести . На пересечении линий и получим оригинал - точку .