- •Лекция №1. Задачи начертательной геометрии. Методы проецирования. Комплексный чертеж точки.
- •1.1. Основные задачи начертательной геометрии (нг)
- •1.2. Методы проецирования
- •1.3. Проецирование точки на две взаимно - перпендикулярные плоскости. Образование комплексного чертежа (эпюр Монжа)
- •1.4. Проецирование точки на три взаимно- перпендикулярные плоскости. Законы проекционной связи.
- •1.5.Алгоритм построения комплексного чертежа точки по заданным координатам на три плоскости проекций
- •Лекция №2. Комплексный чертеж прямой линии
- •2.1. Определение и задание прямой линии в пространстве и на комплексном чертеже
- •2.2. Положение прямой относительно плоскостей проекций
- •Прямая общего положения.
- •Прямые уровня.
- •Проецирующие прямые
- •2.3. Определение натуральной величины отрезка прямой общего положения и углов наклона его к плоскостям проекций
- •2.5. Проекции плоских углов
- •2.5. Взаимное положение точки и прямой.
- •2.6. Взаимное расположение двух прямых в пространстве
1.2. Методы проецирования
Для построения изображений предметов на плоскости в НГ используется метод проецирования. Различают два метода проецирования:
а) центральное;
б) параллельное, которое в свою очередь подразделяется на прямоугольное (ортогональное) и косоугольное.
Центральное проецирование
Наиболее общим методом проецирования является метод центрального проецирования, поскольку он целиком совпадает с процессом нашего зрения, с помощью которого мы воспринимаем окружающий мир. Поэтому рассмотрим суть центрального проецирования на примере рис.1.1.
Допустим,
в пространстве заданная некоторая
плоскость проекций П1
и вне ее границ точка
 - центр проекций. Возьмем также в этом
пространстве произвольные точки
- центр проекций. Возьмем также в этом
пространстве произвольные точки
 ..., которые нужно изобразить на плоскости
П1.
Необходимо сразу предостеречь, что
изображение каждой точки должно быть
определенным и единственным. Тогда,
учитывая то, что через две точки
пространства проходит только одна
прямая и прямая пересекает плоскость
только в одной точке, за проецирующие
линии примем прямые.
..., которые нужно изобразить на плоскости
П1.
Необходимо сразу предостеречь, что
изображение каждой точки должно быть
определенным и единственным. Тогда,
учитывая то, что через две точки
пространства проходит только одна
прямая и прямая пересекает плоскость
только в одной точке, за проецирующие
линии примем прямые.
Итак,
для построения проекции
 некоторой точки
на плоскости П1
через эту точку
и центр проекций
проводят проецирующий луч
некоторой точки
на плоскости П1
через эту точку
и центр проекций
проводят проецирующий луч
 до пересечения с плоскостью проекций
П1
в точке
.
до пересечения с плоскостью проекций
П1
в точке
.
|
Рис.1.1. Центральное проецирование |
При
заданном аппарате проецирования -
зафиксированном положении точки
и плоскости П1,
каждая точка пространства будет иметь
одну и только одну центральную проекцию.
Однако, обратное утверждение: каждой
центральной проекции точки однозначно
отвечает точка пространства, будет не
верно, поскольку, например, множество
точек ,
... прямой
,
... прямой
 (рис. 1.1) имеют одну и ту же проекцию -
.
(рис. 1.1) имеют одну и ту же проекцию -
.
Центральное проецирование имеет ряд свойств, которые сохраняются при любых преобразованиях. Такие свойства называются инвариантами. Отметим главные из них:
1)
Проекция точки, которая не совпадает с
центром проецирования, есть также точка
(рис.1.2):

2)
Если прямая линия не проходит через
центр проецирования, то ее проекцией
также будет прямая линия (рис.1.2):

3) Если прямая линия проходит через центр проецирования, то ее проекцией будет точка (рис.1.2):
|
Рис.1.2. |
4) Если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой (рис.1.3):
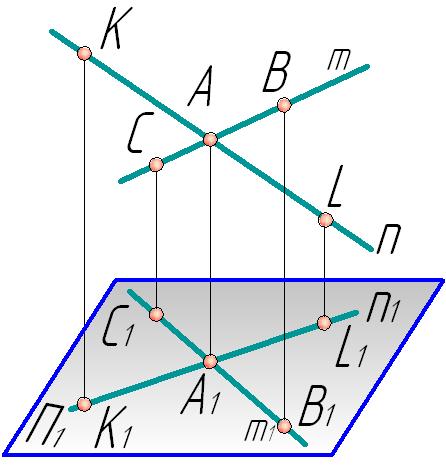
5) Точка пересечения прямых проецируется в точку пересечения их проекций (рис.1.3):
|
Рис.1.3. |
По принципу центрального проецирования работают фотоаппараты и кинокамеры. Упрощенная схема работы человеческого глаза близка к этому виду проецирования: роль центра проецирования выполняет оптический центр хрусталика, роль проецирующих прямых - лучи света; плоскостью проекций служит сетчатка глаза. Поэтому изображения, построенные по принципу центрального проецирования, наиболее наглядны и их широко используют в своей работе художники, архитекторы, дизайнеры и многие другие специалисты.
Однако, центральные проекции не обратимы - невозможно по изображению полностью восстановить геометрические формы предмета.
Параллельное проецирование
Параллельное проецирование можно рассматривать как частный случай центрального, когда центр проецирования удален в бесконечность. В этом случае все проецирующие лучи между собой будут параллельны. В результате этого центральное проецирование перейдет в параллельное (рис.1.4), а бесконечно отдаленный центр будет обозначаться вектором , параллельно которому должны проводиться все проецирующие лучи. Аппарат параллельного проецирования полностью определяется положением плоскости П1 и направлением проецирования .
В общем случае, когда проецирующие лучи с плоскостью проекций П1 составляют угол , который не равняется 90°, параллельное проецирование называется косоугольным (рис.1.4):
|
Рис.1.4. Косоугольное проецирование |
Если угол наклона проецирующего луча составляет с плоскостью проекций 90°, то такое параллельное проецирование называется прямоугольным или ортогональным (рис.1.5):
|
Рис.1.5. Прямоугольное (ортогональное) проецирование |
Параллельное проецирование имеет также название цилиндрического, поскольку совокупность лучей ... в просторные образовывает цилиндрическую поверхность.
При параллельном проецировании сохраняются свойства центрального проецирования и добавляются следующие:
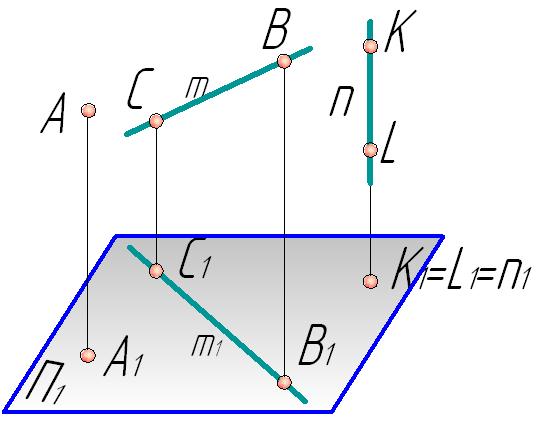
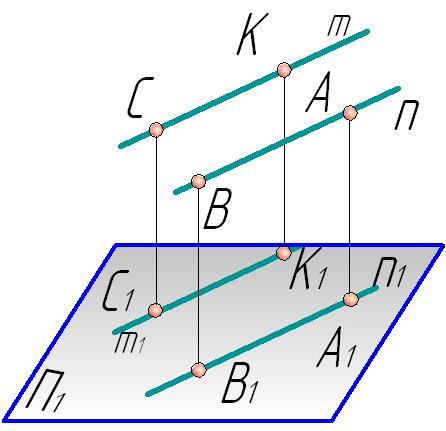
1. Если прямые линии параллельны между собой в пространстве, то параллельны и их проекции (рис.1.6):
|
Рис.1.6. |
2. Если точка
|
Рис.1.7. |
В
параллельном проецировании, как и при
центральном проецировании, каждая точка
пространства при заданном аппарате
проецирования, также имеет одну и только
одну параллельную проекцию. Но, как и
раньше, обратное утверждение не имеет
места, поскольку множество точек
 ...
прямой
(рис. 1.4-1.5) имеют одну и одну и ту же
проекцию -
.
...
прямой
(рис. 1.4-1.5) имеют одну и одну и ту же
проекцию -
.
Поэтому, к проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:
1. Обратимость - восстановление оригинала по его проекционным изображениям (чертежу) - возможность определять форму и размеры объекта, его положение и связь с окружающей средой.
2. Наглядность - чертеж должен создавать пространственное представление о форме предмета.
3. Точность - графические операции, выполненные на чертеже, должны давать достаточно точные результаты.
4. Простота - изображение должно быть простым по построению и должно допускать однозначное описание объекта в виде последовательности графических операций.

 – точки
объекта в пространстве.
– точки
объекта в пространстве. ,
,
 – проецирующие лучи.
– проецирующие лучи. с плоскостью П1).
с плоскостью П1).









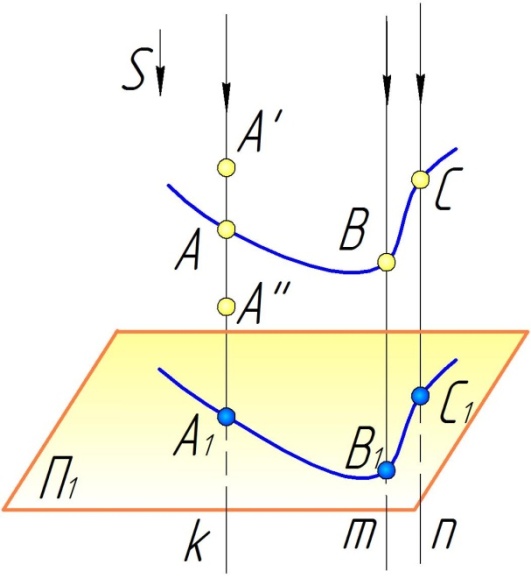

 делит отрезок [
]
в отношении
делит отрезок [
]
в отношении
 ,
то в том же отношении будут разделены
проекции этого отрезка соответствующими
проекциям точки
:
,
то в том же отношении будут разделены
проекции этого отрезка соответствующими
проекциям точки
: