Спочатку використаємо перше правило

Область визначення функції критичними точками ділиться на проміжки: (мал.10). Знайдемо знаки

п охідної в кожному з цих проміжків, підставивши конкретні числа з них в похідну.

Наприклад ,

Отже, в точці максимум.

В точці мінімум.

При застосуванні другого правила знаходимо другу похідну

Підставляємо значення і в другу похідну:

,

В точці максимум , в точці мінімум.

§16. Найменше та найбільше значення функції на відрізку

За теоремою Вейєрштраса неперервна функція на замкнутому відрізку досягає свого найбільшого і найменшого значення. Ці значення функція може досягти на одному з кінців відрізка або всередині відрізка. Тому задачу знаходження найбільшого і найменшого значень функції на відрізку розв’язують так:

1). Знаходять похідну, і прирівнявши її до нуля, знаходять критичні точки першого роду.

2). Обчислюють значення функції в усіх критичних точках, що належать проміжку і значення функції на кінцях відрізка.

3). Серед цих значень вибирають найбільше і найменше значення.

Зауваження. Якщо всередині проміжку функція має тільки одну критичну точку і досягає в ній максимуму, то він буде найбільшим значенням, а якщо досягає в ній мінімуму, то він буде найменшим значенням.

Приклад. Знайти найбільше і найменше значення функції

на проміжку .

Розв’язування. Знаходимо похідну

Прирівнявши похідну до нуля, знаходимо критичні точки першого роду: ,

Оскільки точка не входить в даний проміжок, її до уваги не беремо. Обчислюємо значення функції:

Отже, найбільше значення функції в точці а найменше значення в точці

§17. Приклади задач оптимізації з економічним змістом

З адача 1. На підприємстві з відходів бляшаних листів прямокутної форми розмірами вирішили виготовляти відкриті зверху ящики найбільшого об’єму, вирізавши по кутах рівні квадратики і загнувши бляху, щоб отримати бічні стінки. Якої довжини мають бути сторони вирізаних квадратів?

Розв’язування. Нехай сторони вирізаних квадратів (мал.11).

Тоді розміри ящика будуть і Об’єм ящика

. Знайдемо найбільше значення цієї функції при умові , що . Обчислимо похідну

Прирівнявши її до нуля, знайдемо критичні точки першого роду:

,

,

Оскільки точка не входить у вказаний проміжок, то вона відкидається.

Знайдемо другу похідну

.

Отже, в точці функція досягає максимуму. При і , .

Відповідь: досягається при .

Задача 2. Треба виготовити відкритий циліндричний бак об’єму . Матеріал, з якого виготовляють дно бака коштує гривень за а вартість матеріалу бокової поверхні - гривень за При якому співвідношенні радіуса дна до висоти витрати на матеріал будуть найменшими?

Розв’язування. Нехай радіус основи, а висота бака. Тоді об’єм бака , а витрати на матеріал .

Виразимо з формули об’єму і підставимо у вираз для Z. Одержимо функцію однієї змінної

. Знайдемо похідну

.

Знаходимо критичні точки:

,

друга точка не входить в область визначення функції.

Знайдемо

Отже, в точці функція витрат має мінімум.

Знаходимо : .

Знайдемо відношення : .

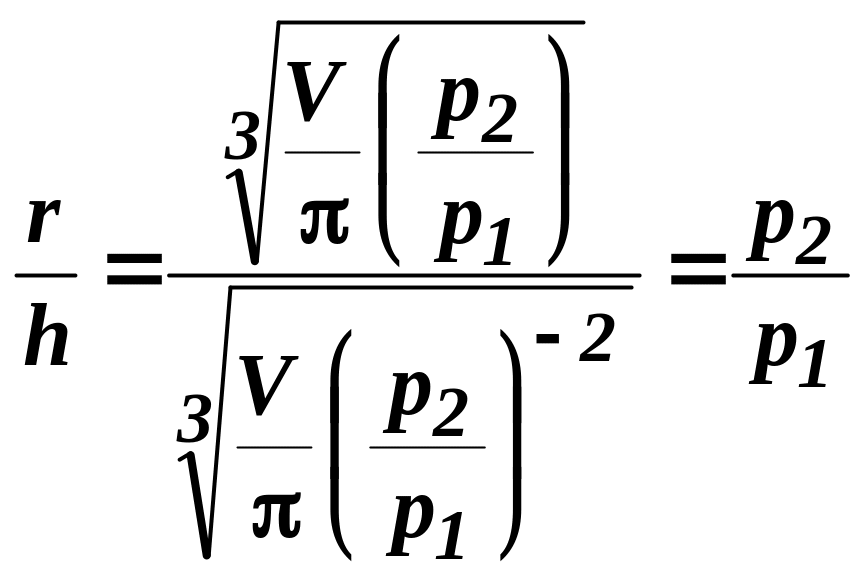Отже, радіус дна до висоти бака повинен відноситись як ціна матеріалу дна до ціни матеріалу бокової поверхні.

Задача 3. Фірма вирішила випускати нові радіоприймачі. Економічним підрозділом фірми встановлено, що при випуску

приймачів щоквартально затрати будуть (гривень), а кількість проданих приймачів в залежності від ціни (гривень) за один приймач становитиме При якому випуску фірма матиме найбільший дохід і прибуток? Який найбільший дохід і прибуток, і при якій ціні, якщо фірма щоквартально може випускати до 5000 приймачів?

Розв’язування. Знайдемо ціну р:

Тоді дохід від реалізації

радіоприймачів

Знайдемо маржинальний дохід і, прирівнявши його до нуля, знайдемо критичні точки:

.

Оскільки а точка єдина входить в даний проміжок [0;5000], то в цій точці D(x) досягає найбільшого значення. (гривень).

Досягається це значення доходу при ціні на приймач

(гривень).

Прибуток шукаємо як різницю між доходом

і витратами :

Знаходимо маржинальний прибуток і, прирівнявши його до нуля, критичні точки:

; ; .

Оскільки , а точка єдина входить в проміжок [0;5000], то в цій точці P(x) досягає найбільшого значення.

(гривень).

З формули прибутку видно, що максимальний прибуток досягається, якщо , тобто коли маржинальні витрати дорівнюють маржинальному доходу.

Максимальний прибуток досягається при випуску і продажі 4050 приймачів по ціні (гривень).

Отже, максимальна виручка (дохід) 675000грн. досягається при випуску і реалізації 4500 радіоприймачів по ціні 150 грн. за приймач, а максимальний прибуток 456750 грн. при випуску і реалі-

зації 4050 радіоприймачів по ціні 165 грн. за приймач.