§5 Похідна від складної функції

Нехай у є функція від аргументу u, тобто y = f(u), і нехай аргумент u є деяка функція від незалежної змінної x: .Тоді y є функція від x: В таких випадках говорять, що у є функція від функції або складною функцією від аргументу x.

Нехай ми вміємо обчислювати похідну від у по аргументу и, а також похідну від аргументу и по незалежній змінній х. Встановимо, як обчислюється похідна від у по незалежній змінній х.

ТЕОРЕМА. Якщо функції і мають

похідні, то похідна складної функції дорівнює похідній від функції у по проміжному аргументу и, помноженій на похідну від проміжного аргументу и по незалежній змінній х.

Тобто, .

Доведення. Надамо x довільний малий приріст Δx. Тоді

функція u=φ(x) дістане приріст Δu, а функція y = f(u) дістане приріст , викликаний приростом . Оскільки похідна за умовою існує, то .

Звідки де разом з .

А тому Розділивши обидві частини рівності

на , маємо . Перейдемо до границі при

і , врахувавши, що внаслідок неперервності функції u , що зумовлює і , одержимо

або ,

що доводить теорему.

Зауваження. В даній теоремі розглянуто складну функцію, де y залежить від x через проміжну змінну u. Можлива і більш складна залежність з двома, трьома і більшим числом проміжних змінних. При цьому правило диференціювання залишається тим же.

Так, наприклад, якщо y=f(u), де u=φ(t), а t=ψ(x), то

.

Приклад 1. Знайти похідну функції y = sin³ x.

Розв’язування.Покладаємо u = sin x , тоді y = u³ .

Звідси , . Отже, .

При певному досвіді проміжний аргумент не пишуть, а використовують його неявно.

Приклад 2. Знайти y′, якщо y = tg ( +4) .

Розв’язування. Пам’ятаючи, що u = x + 4 , знаходимо

.

Приклад 3. Знайти похідну функції

.

Розв’язування. Цю функцію можна розглядати як складну з двома проміжними змінними

де ,

§6. Похідна від оберненої функції

6.1. Поняття оберненої функції і її похідна

Нехай y=f(x) деяка диференційована функція від аргументу x.

Якщо в цьому рівнянні у розглядати як аргумент, а х як функцію, то ця функція , де , називається оберненою до даної функції.

Наша задача, знаючи похідну , знайти .

Теорема 1. Похідна функції , оберненої до даної функції y = f(x) дорівнює величині, оберненій до похідної даної функції, якщо остання не дорівнює нулю.

Тобто, або .

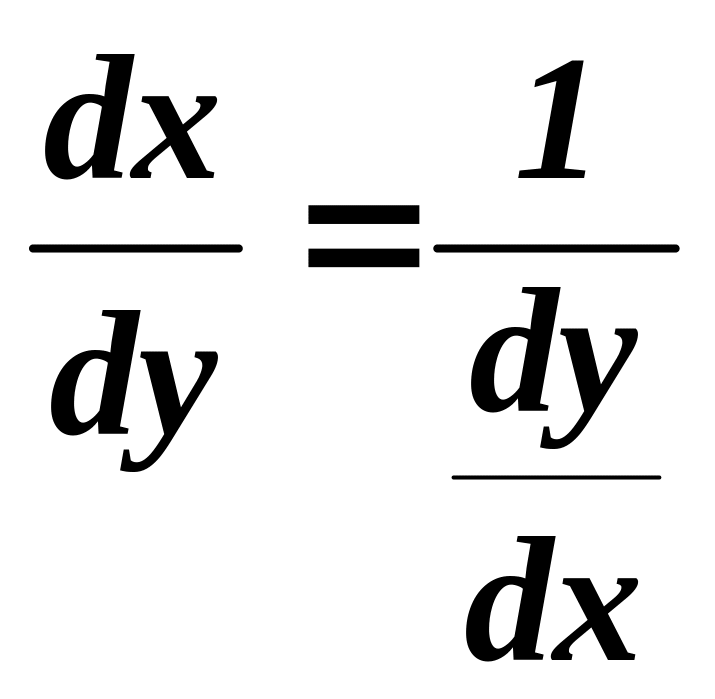Доведення. Нехай дана функція y = f(x) і обернена їй функція . Тоді = .

Отже, х можна розглядати як складну функцію. Диференціюючи цю рівність по х , і враховуючи , що застосовуючи попередню теорему про диференціювання складної функції, маємо

. Звідси або

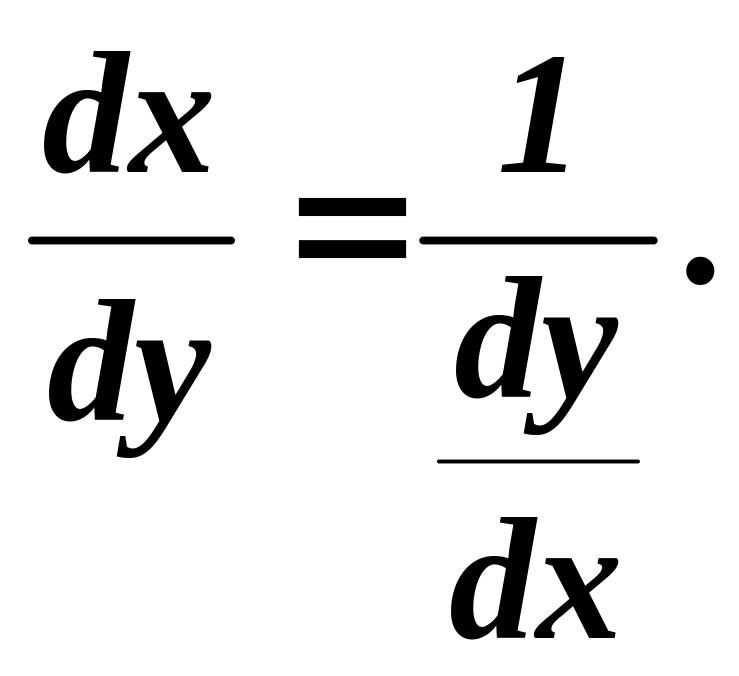
Теорема доведена.

6.2.Похідні від обернених тригонометричних функцій

Наслідок 1. Справедливі формули:

;

Доведення. Якщо , то обернена до неї Оскільки а то .

Виразимо через х. Маємо

Тоді Перед коренем беремо знак

“+”, тому що cos y для всіх додатний. Отже,

.

Аналогічно доводиться .

Наслідок 2. Похідні функцій x, знаходяться за формулами:

; .

Доведення. Оберненою до функції є функція .

Оскільки то

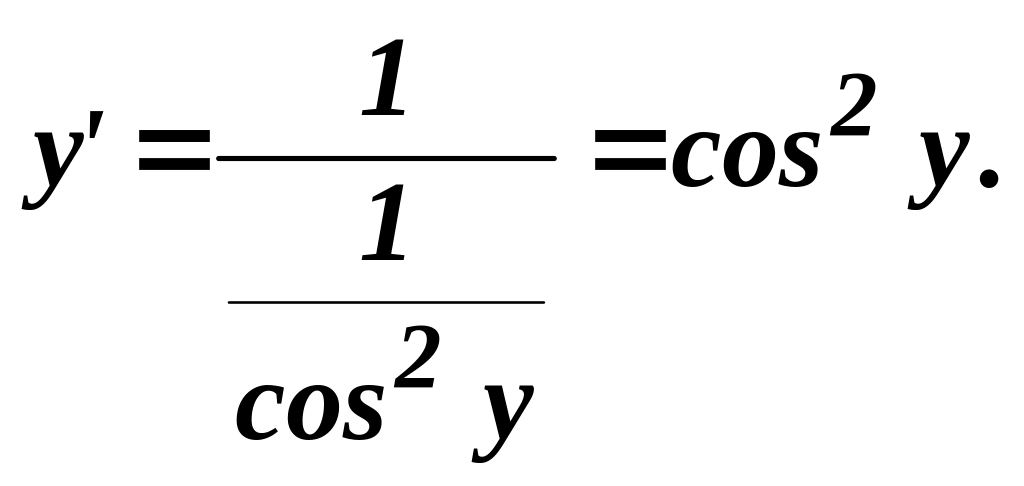
Виразимо через х. Маємо tg y = x. З шкільного курсу відомо Тому .

Отже, = .

Аналогічно доводиться .