§4. Основні правила диференціювання

Знаходження похідних за означенням не проста задача. Тому для відшукання похідних від функцій, які утворені з декількох елементарних функцій використовують правила диференціювання, що сформульовані у вигляді теорем.

ТЕОРЕМА 1. Похідна постійної величини дорівнює .

Доведення. Нехай , де стала.Надаємо довільному приросту .Враховуючи, що функція прийме одне і теж значення при всіх значеннях аргументу, маємо .

Знаходимо відношення приростів .

Похідна цієї функції . Отже .

ТЕОРЕМА 2. Якщо кожна з скінченого числа функцій диференційовна в деякій точці то диференційовною в цій точці є їх алгебраїчна сума, причому похідна алгебраїчної суми цих функцій дорівнює алгебраїчній сумі їх похідних.

.

Доведення. Візьмемо функцію з трьох доданків . Надамо аргументу приріст . Тоді функція та її складові одержать відповідно прирости причому

Складемо відношення приросту функції до приросту аргументу і перейдемо до границі при умові, що . Використавши властивості границь і врахувавши, що похідні функцій існують, одержимо

- або

, що треба було довести.

ТЕОРЕМА 3. Якщо функції і

диференційовні в точці , то їх добуток диференційовний в цій точці і має місце формула .

Доведення. Позначимо . Надамо приросту х

аргументу х. Тоді функції и, ,у одержать відповідно прирости

причому

.

Знайдемо приріст :

Складаємо відношення приростів

Перейдемо до границі при умові , що , використавши властивості границь і врахувавши, що функція неперервна, оскільки вона диференційовна, і тому .

Отже,

= , а тому . Теорема доведена.

Наслідок 1. Сталий множник можна виносити за знак похідної.

Доведення. (Cy)′ = C′y + Cy′ = Cy′ , оскільки

Наслідок 2. Похідна добутку декількох диференційованих функцій дорівнює сумі добутків похідної кожної з цих функцій на всі решта функції співмножники.

Доведення проведемо для випадку трьох співмножників.

.

Приклад. Знайти похідну функції ( натуральне число).

Розв’язування.

= x x x … x .

n – раз

Використовуючи наслідок 2 , маємо

= .

О

n

тже, . (4.2)

ТЕОРЕМА 4. Якщо функції

диференційовні в точці , причому , то їх частка

також має похідну в цій точці, яка обчислюється за формулою:

.

Доведення. Позначимо . Надамо аргументу приросту

. Тоді одержать відповідно прирости , причому . Знайдемо приріст :

.

Складемо відношення приростів .

Перейдемо до границі при умові, що , використавши властивості границь і врахувавши, що функція неперервна, оскільки вона диференційовна, і тому .

Отже,

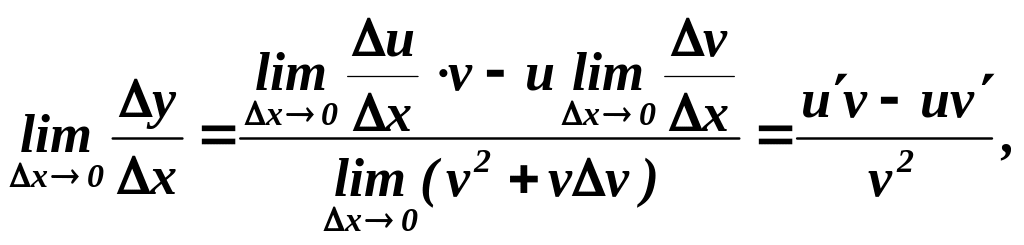
а тому . Теорема доведена.

Наслідок 3. Якщо знаменник дробу постійна величина, то

.

Дійсно,

Наслідок 4. Якщо чисельник дробу – постійна величина, то

Зокрема, при маємо .

Наслідок 5. (похідні функцій ).

Справедливі формули:

; , .

Доведення.

=

= , що треба довести.

Приклади.

1.Знайти похідні функцій:

а) .

Розв’язування. Використовуючи послідовно теорему 2,

наслідок 1 і формулу похідних від степеня (4.2), одержимо:

а)

= .

б) .

Розв’язування. Використовуючи теорему 3, одержимо

+ .

в) .

Розв’язування. Використовуючи теорему 4 і наслідок 5, одержимо

=

= .

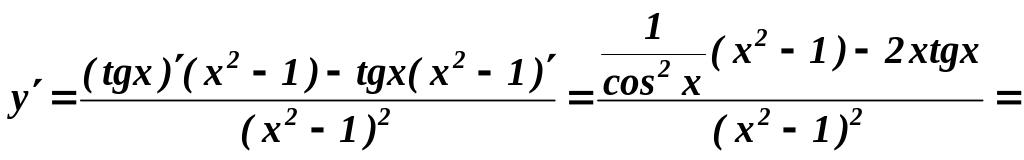
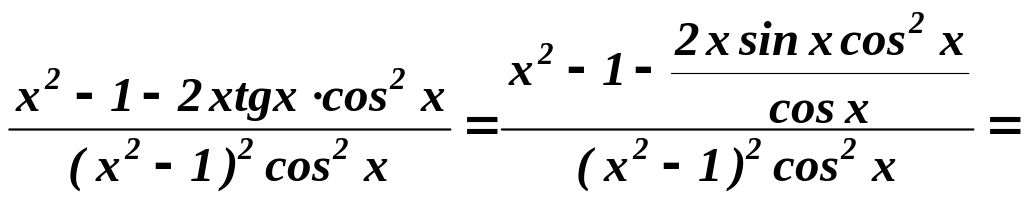
2.Економічним підрозділом підприємства встановлено, що витрати виробництва одиниць продукції виражаються формулою (у гривнях). V(x)=0,01x²+40x+2000.

Знайти маржинальні (граничні) витрати та середні витрати і обчислити їх при х=200.

Розв’язування. Маржинальні витрати для довільної кількості виготовленої продукції визначаються як похідна від функції витрат

. При маємо

.

Середні витрати на одиницю продукції .

При , одержимо

Проаналізувавши одержані результати, можна зробити висновок, що при середніх витратах на виробництво одиниці продукції в розмірі 52 грн., додаткові витрати на виробництво одиниці додаткової продукції складуть 44 грн. і не перевищать середніх витрат.

3. Визначити маржинальний дохід і прибуток підприємства, якщо місячні витрати на виготовлення і реалізацію одиниць продукції виражаються формулою , а кількість реалізованих виробів в залежності від роздрібної ціни визначаються формулою .Знайти маржинальний дохід і прибуток при виробництві одиниць продукції.

Розв’язування. Визначимо роздрібну ціну одиниці продукції , .

Дохід підприємства буде

, а прибуток

=

Маржинальний дохід

а маржинальний прибуток

При x=500 маємо D′(500)=400-0,2∙500=400-100=300,

P′(500)=300-0,24∙500=300-120=180.