Розділ 4. Диференціальне числення функцій однієї змінної

Закономірності, які вивчають різні галузі науки, в тому числі й економіки, описуються за допомогою функцій. Описавши процес функцією, дослідження процесу зводиться до вивчення властивостей функції. Відповідь на такі питання , як швидкість процесу в даний момент, проміжки часу, коли буде прискорення чи уповільнення процесу та інші можна одержати за допомогою похідної даної функції.

§1. Означення похідної

Уточнимо поняття похідної функції, з яким знайомі з шкільного курсу математики.

Нехай задано функцію визначену на проміжку Візьмемо деяку точку з цього проміжку. Значення функції в ній буде Hадамо аргументу приріст х, такий, що точка не вийде за вказаний проміжок.Тоді функція одержить нове значення , а її приріст . Складемо відношення

приросту функції до приросту аргументу

. (4.1)

Знайдемо границю відношення (4.1) при умові, що прямує до нуля. Якщо ця границя існує, то її називають похідною функції в точці і позначають .

.

Якщо похідна існує для всіх точок проміжку,то вона є функцією від х . Для кожного конкретного значення похідна є число.

Означення. Похідною функції у = f(x) в точці х називається границя відношення приросту функції в цій точці до приросту аргументу, коли приріст аргументy прямує до нуля.

Похідну позначають так:

.

Покажемо застосування цього означення для знаходження похідних деяких функцій.

Приклад 1. Знайти похідну функції .

Розв’язування.

1. Надаємо аргументу х приросту х.

2. Знаходимо приріст функції , віднявши від значення функції в новій точці значення функції в початковій точці

3. Складаємо відношення приростів

4. Обчислюємо границю цього відношення при умові , що приріст аргументу прямує до нуля

.

Отже, або .

Приклад 2. (самостійно). Знайти похідну функції . Відповідь:

Приклад 3. Знайти похідну функції у=sin x.

Розв’язування.

1. Надаємо довільному х приросту .

2. Знаходимо приріст функції

(x+

3. Складаємо відношення приростів

4. Обчислюємо границю цього відношення при умові , що

.

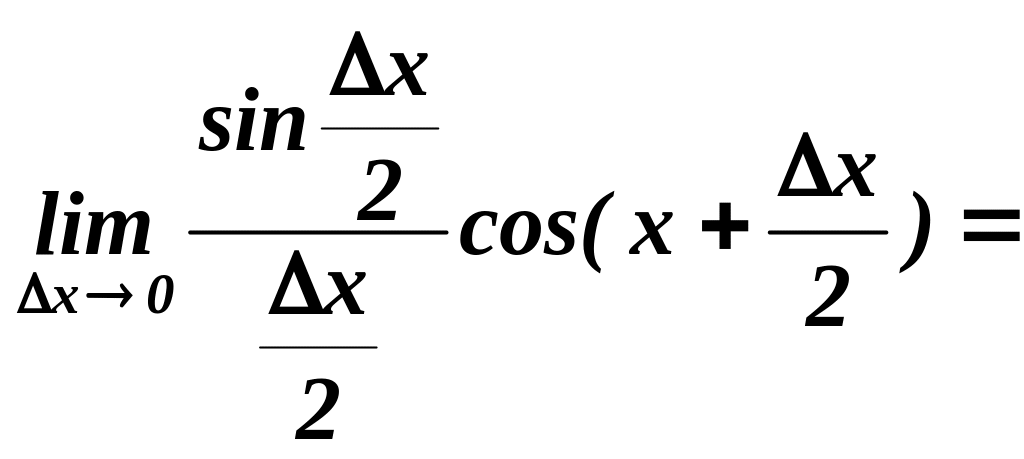
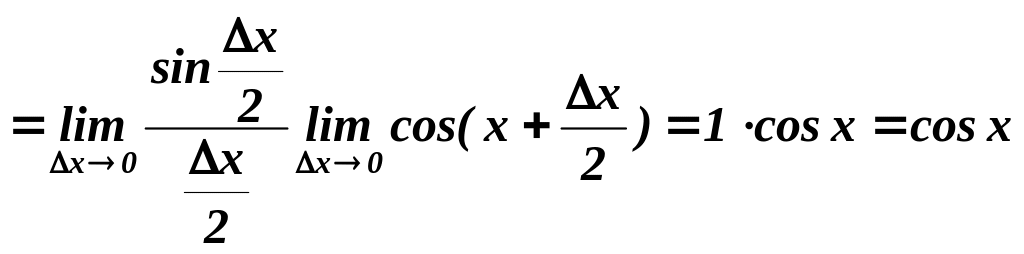Отже, (sin x) = cos x.

Таким способом можна довести, що .

§2. Задачі, що приводять до поняття похідної

2.1.Геометричний зміст похідної

О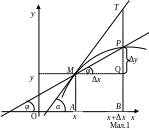 днією з задач геометрії, яка тісно пов’язана з історією виникнення диференціального числення є задача про проведення дотичних до кривих.

Означення. Дотичною до кривої, заданої рівнянням в точці дотику називають граничне положення січної , коли точка , рухаючись по кривій прямує до точки .

Розглянемо графік y=f(x). Візьмемо на графіку точку М(x,y) і другу точку Р( Проведемо січну МР і позначимо кут нахилу її до додатнього напрямку осі через . Позначимо кут, який утворює дотична з додатнім напрямом осі через .

Якщо пересувати точку Р по кривій до точки М, то граничним положенням січної МР буде дотична МТ до графіка в точці М. Як видно з

малюнка f( ),

.

Отже, ,

а .

Отже, похідна в даній точці x дорівнює тангенсові кута, утвореного дотичною до графіка функції в точці з додатнім напрямом осі . Інакше, похідна в точці x дорівнює кутовому коефіцієнту дотичної до графіка функції в точці