Завдання 4

Є наступні дані про внутрішньорічну динаміку чисельності працівників організації по кварталах за три роки, чол.:

Квартали	2008*	2009*	2010*
I	157	152	147
II	145	131	119
III	151	137	131
IV	159	157	155

* Чисельність працівників + № варіанту

Провести аналіз внутрішньорічної динаміки чисельності працівників організації, для чого:

1. Визначити індекси сезонності методом постійної середньої.

2. Зобразити на графіці сезонну хвилю зміни чисельності працівників. Зробити висновки.

3. Здійснити прогноз чисельності працівників організації на 2011 р. по кварталах на основі розрахованих індексів сезонності за умови, що середньорічна чисельність працівників в прогнозованому році складе 167 чоловік(160 чол. + 7).

8.1. Дослідження структури сукупності

Для побудови ряду розподілу необхідно визначити ознаку - середньооблікова чисельність працівників (таблиця 2.1.) і відсортувати ці дані (таблиця 2.2).

Таблиця 2.1

Початкові дані

№ п/п	Середньооблікова чисельність, чол. (У)
1	201
2	190
3	192
4	191
5	193
6	192
7	193
8	189
9	190
10	193
11	188
12	189
13	190
14	196
15	194
16	192
17	191
18	190
19	191
20	190
21	190
22	191
23	193
24	192
25	194
26	190
27	196
28	199
29	200
30	203

Таблиця 2.2

Відсортовані дані

№ п/п	Середньооблікова чисельність, чол.(У)
1	188
2	189
3	189
4	190
5	190
6	190
7	190
8	190
9	190
10	190
11	191
12	191
13	191
14	191
15	192
16	192
17	192
18	192
19	193
20	193
21	193
22	193
23	194
24	194
25	196
26	196
27	199
28	200
29	201
30	203

Ряд розподілу - це угрупування, що є розподілом чисельності одиниць сукупності за значенням якої-небудь ознаки, в нашому випадку за ознакою - середньооблікова чисельність працівників. Якщо ряд побудований за кількісною ознакою, його називають варіаційним. При побудові варіаційного ряду з рівними інтервалами визначають число груп (n) і величину інтервалу (h). По умові завдання необхідно утворити п'ять груп (n=5). Величина рівного інтервалу розраховується по формулі:

,

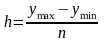де y_max и y_min – максимальне і мінімальне значення ознаки.

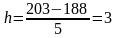_чол.

Величина інтервалу рівна 3. Звідси шляхом збільшення величини інтервалу до мінімального рівня ознаки в групі отримаємо наступні групи організацій за середньообліковою чисельністю (таблиця 2.3.).

Таблиця 2.3.

№ інтервалу	Група п/п	Число п/п
		в абсолютному вигляді	у відносному вигляді , %
1	188-191	10	33,33
2	191 - 194	12	40
3	194- 197	4	13,33
4	197 -200	1	3,34
5	200 - 203	3	10
Разом		30	100

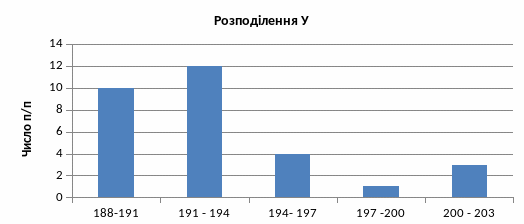
Дані угрупування показують, що 40 % організацій мають середньооблікову чисельність працівників 192 чол.

Мода (Мо) - це значення випадкової величини, що зустрічається з найбільшою вірогідністю в дискретному варіаційному ряді, - це варіант, що має найбільшу частоту. У інтервальному варіаційному ряді мода обчислюється за формулою:

,

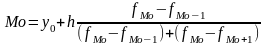де y₀ – нижня межа модального інтервалу;

h – розмір модального інтервалу;

f_Mo – частота модального інтервалу;

f_Mo-1 – частота інтервалу, що стоїть перед модальною частотою;

f_Mo+1 – частота інтервалу, що стоїть після модальної частоти.

Звідси: 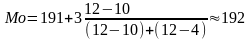чол.

Графічне знаходження моди:

Медіана (М_е) – це величина ознаки, яка знаходиться в середині ранжируваного ряду, тобто розташованого в порядку зростання або спадання.

Для інтервального варіаційного ряду М_е розраховується по формулі:

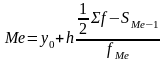
де y₀ – нижня межа медіанного інтервалу;

h – нижня межа медіанного інтервалу;

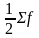- половина від загального числа спостережень;

S_Me-1 – сума спостережень,які накопичені до медіанного інтервалу;

f_Me – частота медіанного інтервалу.

Визначуваний медіанний інтервал, в якому знаходиться порядковий номер медіани (n).

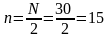
У графі “Сума накопичених спостережень” таблиці 2.4. значення 15 відповідає інтервалу №2, тобто 191- 194. Це і є медіанний інтервал, в якому знаходиться медіана.

Звідси: 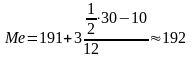чол.

Таблиця 2.4.

№ інтервалу	Група п/п	Число п/п		Сума накопичених часток (S)	Середина інтервалу, Yi
		в абсолютному вигляді	у відносному вигляді, %
1	188-191	10	33,33	10		189,5
2	191 - 194	12	40	22		192,5
3	194- 197	4	13,33	26		195,5
4	197 -200	1	3,34	27		198,5
5	200 - 203	3	10	30		201,5
Разом		30	100

Графічне знаходження медіани:

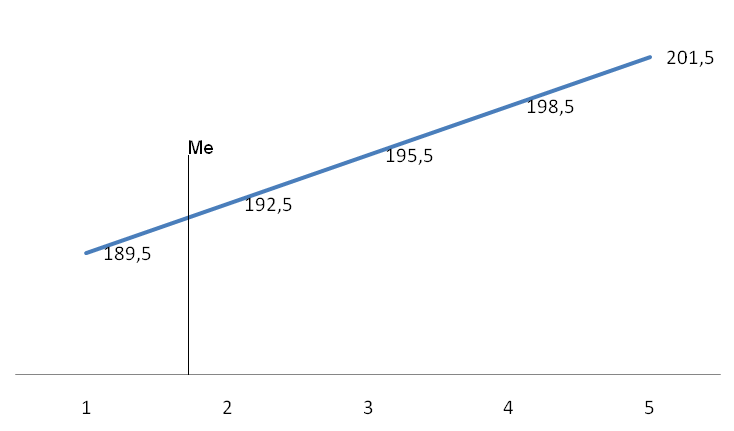
Розрахуємо характеристики ряду розподілу.

Для розрахунку необхідно визначити середини інтервалів розподілу середньооблікової чисельності працівників (таблиця 2.5.).

Таблиця 2.5.

Група п/п	Середина інтерва-лу, Yi	Кількість п/п, Ni	Yi * Ni	Yi - Ycp	(Yi - Ycp)2 * Ni
188-191	189,5	10	1895	-3,5	122,5
191 - 194	192,5	12	2310	-0,5	3
194- 197	195,5	4	782	2,5	25
197 -200	198,5	1	198,5	5,5	30,25
200 - 203	201,5	3	604,5	8,5	216,75
Разом		30	5790		397,5

Середня арифметична зважена визначається по формулі:

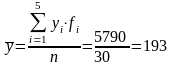чол., де

y – варіанти або середини інтервалів варіаційного ряду;

f – відповідна їм частота;

Середнім квадратичним відхиленням є корінь квадратний з дисперсії і він дорівнює:

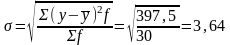чол.

Тобто в середньому середньооблікова чисельність працівників по організаціях коливається в межах ± 3,64 чол. від його середнього значення 193 чол.

Коефіцієнтом варіації є процентне відношення середнього квадратичного відхилення до середньої арифметичної:

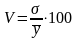
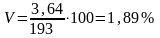
На підставі отриманого коефіцієнта варіації можна зробити висновок, що за рівнем середньооблікової чисельності працівників організації дані є однорідними, оскільки коефіцієнт не перевищує 33%.

Обчислимо середню арифметичну за початковими даними таблиці 1. Середня арифметична проста дорівнює сумі значень ознаки, що ділиться на їх кількість:

,

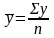де y – значення ознаки;

n – кількість одиниць ознаки.

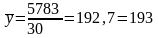чол.

Розбіжності між арифметичною середньою простою і зваженою виникли через те, що арифметична середня зважена визначається за згрупованими даними.