3.2. Решение системы уравнений

После выяснения совместности системы строят ее общее решение. Для этого вновь полученную после элементарных преобразований матрицу записывают в виде системы, отбросив нулевые строки. Количество уравнений в этой системе определяет количество основных неизвестных. Все остальные неизвестные считаются свободными, им придаются произвольные значения. В качестве основных неизвестных берут неизвестные при ступенчато-диагональных элементах.

Примеры.

а) Построим общее решение системы из первого примера предыдущего пункта. После элементарных преобразований (см. выше) получаем систему

.

Уравнений два, поэтому считаем х₁ и х₂ (стоящие при ступенчато-диаго-нальных элементах) основными, а х₃ и х₄ свободными. Находим из системы основные неизвестные через свободные:

,

.

Таким образом, общее решение системы имеет вид:

б) Решим систему

Записываем расширенную матрицу системы и преобразуем ее

Выбираем в качестве основных переменные х₁ и х₃, как стоящие при ступенчато-диагональных элементах, переменная х₂ берется свободной. Итак,

и общее решение системы

3.3. Задачи для самостоятельного решения

Исследовать и в случае совместности решить предлагаемые ниже системы линейных уравнений.

Задача 1) Задача 2)

Задача 3)

4. Векторы, простейшие действия над ними

4.1. Основные понятия

Понятие вектора известно из школьного курса. Наиболее часто мы будем пользоваться координатной формой записи векторов: . Напомним, что всегда вектор предполагается свободным, т.е. его можно без изменения длины и направления переносить в любую точку пространства. В случае координатного задания вектора его длина вычисляется по формуле:

. (4.1)

Направление же вектора определяется углами , , , образованными вектором с положительными полуосями координат Ох, Оу, Oz, которые можно найти из формул для направляющих косинусов этих углов:

(4.2)

4.2. Операции над векторами

Произведение вектора на скалярный множитель  определяется по формуле  = (а₁, а₂, а₃).

Для двух векторов , их сумма и разность определяются по правилам:

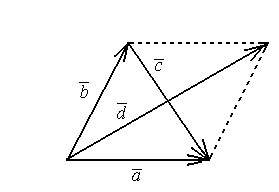
Геометрически сумма и разность векторов строится как на рис. 1.

Рис. 1

Если точка О – начало координат, а М – точка с координатами (x, y, z), то вектор называется радиусом-вектором точки М.

Вектор с началом в точке А(x₁, y₁, z₁) и концом в точке В(x₂, y₂, z₂) в координатном виде записывается так: = .

Примеры.

а) В треугольнике АВС сторона АВ точками М и N разделена на три равные части: Найти вектор , если . Если построить треугольник и указанные вектора, то из геометрических правил сложения и вычитания легко получаются равенства т.е. . Так как , то Та-ким образом,

б) Найти длину вектора = (10, 15, -30) и его направляющие косинусы.

По формулам (4.1) и (4.2) определяем

в)Найти вектор , если А(2, 1, 0) и В(3, 0, 5).

Из формулы для координат вектора имеем = (3-2, 0-1, 5-0) =

= (1, -1, 5).