
- •Isbn 978–5–4221–0442-0
- •Isbn 978–5–4221–0442-0 Уфимский государственный
- •Оглавление
- •Вычисление определителей
- •1.1. Определители второго порядка
- •1.2. Определители третьего порядка
- •Задачи для самостоятельного решения
- •1.4. Определители произвольного порядка
- •2.5. Задачи для самостоятельного решения
- •2.6. Обратная матрица
- •Найдем разность матриц
- •2.7. Задачи для самостоятельного решения
- •3. Решение систем уравнений
- •3.1. Линейные системы уравнений
- •Матрицы
- •3.2. Решение системы уравнений
- •3.3. Задачи для самостоятельного решения
- •4. Векторы, простейшие действия над ними
- •4.1. Основные понятия
- •4.2. Операции над векторами
- •4.3. Задачи для самостоятельного решения
- •5. Скалярное произведение векторов
- •5.1. Определение скалярного произведения и его свойства
- •5.2. Задачи для самостоятельного решения
- •6. Векторное произведение
- •6.1. Определение векторного произведения
- •6.2. Свойства векторного произведения
- •6.3. Задачи для самостоятельного решения
- •7. Смешанное произведение векторов
- •7.1. Определение смешанного произведения и его свойства
- •7.2. Задачи для самостоятельного решения
- •8. Прямая на плоскости
- •8.1. Различные виды уравнений прямой на плоскости
- •8.2. Задачи для самостоятельного решения
- •8.3. Нормальное уравнение прямой. Расстояние от точки до прямой
- •8.4. Геометрические задачи с использованием различных
- •8.5. Задачи для самостоятельного решения
- •9. Прямая и плоскость в пространстве
- •9.1. Плоскость в пространстве
- •9.2. Задачи для самостоятельного решения
- •9.3. Прямая и плоскость
- •9.4. Задачи для самостоятельного решения
- •10. Кривые второго порядка на плоскости
- •11. Введение в анализ
- •11.1. Предел функции. Основные определения и обозначения
- •11.2. Неопределенности вида 0/0
- •11.3. Неопределенности вида /
- •11.4. Неопределенности вида - , 0, 00, 0, 1
- •11.5. Непрерывность функции в точке. Классификация точек разрыва
- •12. Дифференциальное исчисление функций одной переменной
- •12.1. Производная функции. Основные определения и обозначения
- •12.2. Правило Лопиталя
- •12.3. Геометрические приложения производной
- •13. Исследование функций и построение графиков
- •13.1. Возрастание и убывание функций. Экстремум
- •13.2. Направление выпуклости и точки перегиба
- •13.3. Асимптоты
- •13.4. Построение графиков функций
- •14. Дифференциальное исчисление функций нескольких переменных
- •14.1. Предел и непрерывность функции нескольких переменных
- •14.2. Частные производные
- •14.3. Дифференциал
- •14.4. Экстремумы функций нескольких переменных
- •1) Параллельно данной прямой;
- •Список литературы
1) Параллельно данной прямой;
2) перпендикулярно данной прямой.
Исходные данные взять из табл. 1.
Таблица 1
№ вари- анта |
А |
В |
С |
М0 |
А1 |
В1 |
С1 |
D1 |
А2 |
В2 |
С2 |
D2 |
М1 |
1 |
1 |
-2 |
5 |
3;-1 |
5 |
-3 |
1 |
-18 |
2 |
-1 |
-1 |
-2 |
1;1;0 |
2 |
2 |
3 |
3 |
-2;3 |
-2 |
-1 |
0 |
1 |
0 |
6 |
2 |
6 |
1;0;2 |
3 |
2 |
-4 |
1 |
7;5 |
3 |
4 |
5 |
-26 |
3 |
-3 |
-2 |
-5 |
0;0;1 |
4 |
5 |
0 |
3 |
2;3 |
5 |
0 |
3 |
18 |
0 |
-5 |
1 |
11 |
2;1;-1 |
5 |
1 |
5 |
0 |
-3;7 |
1 |
-2 |
1 |
-3 |
1 |
1 |
-1 |
2 |
1;2;2 |
6 |
-2 |
0 |
9 |
4;5 |
3 |
2 |
0 |
8 |
2 |
0 |
2 |
-2 |
2;3;5 |
7 |
3 |
3 |
4 |
1;-2 |
3 |
-2 |
1 |
3 |
4 |
-3 |
4 |
1 |
1;-1;-1 |
8 |
2 |
7 |
3 |
2;-1 |
2 |
-2 |
1 |
3 |
3 |
-2 |
2 |
17 |
2;3;-1 |
9 |
5 |
6 |
7 |
3;-2 |
2 |
-3 |
0 |
0 |
0 |
-2 |
-2 |
14 |
1;-5;3 |
10 |
4 |
6 |
5 |
0;10 |
1 |
-1 |
-1 |
-22 |
2 |
2 |
-1 |
-10 |
-7;5;9 |
11 |
2 |
4 |
3 |
5;-5 |
3 |
1 |
3 |
7 |
5 |
-3 |
2 |
5 |
-3;2;5 |
12 |
2 |
-3 |
-3 |
1;-7 |
1 |
-2 |
3 |
-5 |
1 |
-2 |
-4 |
3 |
3;-4;-6 |
13 |
-3 |
4 |
5 |
-9;1 |
2 |
-1 |
1 |
-3 |
1 |
2 |
-1 |
-5 |
2;5;7 |
14 |
1 |
-3 |
8 |
3;4 |
3 |
2 |
0 |
1 |
0 |
4 |
3 |
-7 |
0;0;5 |
15 |
5 |
1 |
1 |
4;2 |
4 |
-1 |
-5 |
4 |
2 |
1 |
-4 |
2 |
3;-2;0 |
16 |
4 |
-1 |
5 |
7;0 |
1 |
1 |
-3 |
-1 |
2 |
-1 |
-9 |
-2 |
7;0;3; |
17 |
-4 |
2 |
1 |
1;-2 |
2 |
1 |
2 |
5 |
2 |
-2 |
-1 |
2 |
-3;60 |
18 |
2 |
5 |
-3 |
2;8 |
1 |
-6 |
-6 |
2 |
2 |
2 |
9 |
-1 |
4;0;0 |
19 |
0 |
6 |
1 |
1;3 |
1 |
-1 |
-4 |
-5 |
2 |
1 |
-2 |
-4 |
3;0;4 |
20 |
1 |
3 |
2 |
4;-5 |
3 |
2 |
-5 |
-4 |
1 |
-2 |
3 |
-4 |
0;5;1 |
21 |
5 |
-1 |
3 |
0;0 |
5 |
1 |
1 |
0 |
2 |
3 |
-2 |
5 |
0;0;0 |
22 |
7 |
1 |
-15 |
1;1 |
2 |
-1 |
1 |
1 |
1 |
2 |
-1 |
-6 |
1;2;2 |
23 |
3 |
-2 |
-13 |
1;-2 |
5 |
-2 |
-1 |
3 |
-2 |
-1 |
1 |
-1 |
2;3;-1 |
24 |
5 |
7 |
3 |
2;-3 |
1 |
3 |
1 |
2 |
1 |
-1 |
-3 |
-2 |
3;-5;7 |
25 |
1 |
5 |
-7 |
-2;1 |
1 |
1 |
-3 |
1 |
1 |
-1 |
1 |
3 |
2;4;-6 |
Задача 3. Для матрицы третьего порядка вычислить ее определитель; найти ее обратную матрицу:

Задача 4) Найти определитель четвертого порядка:



Задача 5) Для прямых Ах + Ву + С = 0 и А1х + В1у + С1 = 0 найти их взаимное расположение. В случае их пересечения найти угол между ними, в случае их параллельности – расстояние. Исходные данные взять из табл. 1.
Задача 6) Даны вершины треугольника с координатами (А, А1), (В, В1) и (С, С1). Найти уравнения высоты и медианы этого треугольника (на ваш выбор). Исходные данные взять из табл. 1.
Задача 7) Вычислить расстояние от точки М1 до плоскости А1х + В1у + С1z + D1 = 0. Исходные данные взять из табл. 1.
Задача 8) Найти угол между плоскостями А1х + В1у + С1z + D1 = 0 и А2х + В2у + С2z + D2 = 0. Исходные данные взять из табл. 1.
Задача 9) Найти точку Q, симметричную точке М1 относительно прямой
![]()
Исходные данные взять из табл. 1.
Задача 10) Написать уравнение прямой, проходящей через точки (x0, y0, z0) и P. Исходные данные взять из табл. 2.
Задача
11) Вычислить расстояние d
от точки Р
до прямой
![]() Исходные данные взять в табл. 2.
Исходные данные взять в табл. 2.
Задача
12) По координатам вершин пирамиды
![]() найти: 1) длины ребер
найти: 1) длины ребер
![]() и
и
![]() ;
2) угол между ребрами
и
;
2) угол между ребрами
и
![]() ;
3) площадь грани
;
3) площадь грани
![]() ;
4) объем пирамиды; 5) уравнение
прямых
;
4) объем пирамиды; 5) уравнение
прямых
![]() и
;
и
;
6)
уравнения плоскостей
![]() и
и
![]() ;
7) угол между плоскостями
и
;
7) угол между плоскостями
и
![]() ;
;
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
Таблица 2
№ варианта |
(x0,y0,z0) |
(l,m,n) |
P |
№ варианта |
(x0,y0,z0) |
(l,m,n) |
P |
1 |
1;-1;7 |
2;-3;3 |
1;2;-3 |
14 |
1;-1;0 |
1;-2;6 |
1;0;-1 |
2 |
-5;2;-3; |
3;-2;-1 |
1;-2;5 |
15 |
-2;1;3 |
-2;3;2 |
4;3;0 |
3 |
-3;-2;8 |
3;2;-2 |
-1;1;0 |
16 |
2;-1;5 |
3;-4;4 |
2;1;0 |
4 |
-7;5;9 |
3;-1;4 |
2;0;-2 |
17 |
5;-3;5 |
-2;2;-1 |
3;0;-1 |
5 |
1;-2;5 |
2;-3;4 |
0;2;3 |
18 |
-2;0;1 |
2;-3;4 |
3;1;7 |
6 |
7;2;1 |
3;2;-2 |
0;2;3 |
19 |
3;-2;0 |
1;-1;2 |
1;2;-7 |
7 |
5;6;-3 |
13;1;-4 |
3;-4;-2 |
20 |
0;1;0 |
1;-2;3 |
3;3;5 |
8 |
2;3;-3 |
2;-3;2 |
0;0;0 |
21 |
3;2;-6 |
2;3;-4 |
5;-1;-4 |
9 |
-4;4;-1 |
2;-1;-2 |
3;3;1 |
22 |
5;-1;-4 |
1;-4;1 |
3;2;-6 |
10 |
-5;5;5 |
4;-3;-5 |
1;0;2 |
23 |
1;-2;1 |
2;3;-6 |
0;5;6 |
11 |
2;-4;1 |
3;-2;2 |
3;-2;-4 |
24 |
3;5;-2 |
-4;3;-12 |
2;2;3 |
12 |
5;-3;-1 |
2;-4;3 |
4;2;-1 |
25 |
1;-1;3 |
3;2-5 |
-1;2;-3 |
13 |
9;0;2 |
6;-2;-1 |
-5;-5;1 |
|
|
|
|
Задача 13) Решить задачу по теории кривых 2-го порядка:
1.
Составьте каноническое уравнение
эллипса, если его малая ось равна 24, а
расстояние между фокусами
![]()
2.
Составьте каноническое уравнение
гиперболы, если ее фокусы находятся в
точках
![]() а её эксцентриситет
а её эксцентриситет
![]()
3. Составить каноническое уравнение
гиперболы, если известны её эксцентриситет
![]() ,
фокус
,
фокус
![]() и уравнение соответствующей директрисы
5х–16=0.
и уравнение соответствующей директрисы
5х–16=0.
4. Составить каноническое уравнение
эллипса, если известны его эксцентриситет
![]() ,
фокус
,
фокус
![]() и уравнение соответствующей директрисы
х–6=0.
и уравнение соответствующей директрисы
х–6=0.
5.
Составьте каноническое уравнение
гиперболы, фокусы которой лежат на оси
абсцисс симметрично относительно начала
координат и даны уравнения асимптот
![]() и уравнения директрис
и уравнения директрис
![]()
6.
Прямая
![]() касается гиперболы, фокусы которой
находятся в точках
касается гиперболы, фокусы которой
находятся в точках
![]() Составить уравнение этой гиперболы.
Составить уравнение этой гиперболы.
7.
Эксцентриситет гиперболы
![]() ,
расстояние от точки М
гиперболы до директрисы равно 4. Вычислить
расстояние от точки М
до фокуса, одностороннего с этой
директрисой.
,
расстояние от точки М
гиперболы до директрисы равно 4. Вычислить
расстояние от точки М
до фокуса, одностороннего с этой
директрисой.
8.
Убедившись, что точка
![]() лежит на гиперболе
лежит на гиперболе
![]() ,
определить фокальные радиусы точки М.
,
определить фокальные радиусы точки М.
9.
Найти точки гиперболы
![]() ,
расстояние от которых до левого
фокуса равно 7.
,
расстояние от которых до левого
фокуса равно 7.
10.
Найти расстояние от правого фокуса
гиперболы
![]() до её асимптот.
до её асимптот.
11.
Написать уравнение окружности, имеющей
центр в фокусе параболы
![]() и касающейся её директрисы. Найти точки
пересечения параболы и окружности.
и касающейся её директрисы. Найти точки
пересечения параболы и окружности.
12.
Написать каноническое уравнение
гиперболы, имеющей эксцентриситет
![]() и проходящей через точку
и проходящей через точку
![]() .
.
13. Найти эксцентриситет эллипса, если расстояние между фокусами равно расстоянию между концами большой и малой полуосей.
14.
Найти эксцентриситет гиперболы, асимптота
которой составляет с вещественной осью
угол
![]() .
.
15.
Составить каноническое уравнение
эллипса, зная, что большая ось равна
![]() ,
а расстояние между фокусами
,
а расстояние между фокусами
![]() .
.
16.
Привести к каноническому виду уравнение
![]() .
Найти полуоси, эксцентриситет, уравнения
директрис.
.
Найти полуоси, эксцентриситет, уравнения
директрис.
17.
Привести к каноническому виду уравнение
![]() .
Найти полуоси, эксцентриситет, уравнения
директрис.
.
Найти полуоси, эксцентриситет, уравнения
директрис.
18.
Привести к каноническому виду уравнение
![]() .
Нарисовать кривую.
.
Нарисовать кривую.
19. Написать каноническое уравнение эллипса, если и расстояние между директрисами равно 5.
20.
Составьте каноническое уравнение
гиперболы, если
и
![]() .
.
21.
Вычислить расстояние от точки М, лежащей
на параболе
![]() ,
до фокуса параболы, если
,
до фокуса параболы, если
![]() .
.
22.
На эллипсе, симметричном относительно
осей координат, даны точки
![]() и
и
![]() Написать уравнение эллипса и найти
расстояние от точки
Написать уравнение эллипса и найти
расстояние от точки
![]() до фокусов.
до фокусов.
23.
Составить уравнение гиперболы,
симметричной относительно осей координат,
если она проходит через точки
![]() и
и
![]()
24.
Составить каноническое уравнение
параболы, если ее фокус находится в
точке пересечения прямой
![]() с осью
с осью
![]()
25.
Составить каноническое уравнение
эллипса, если
![]() ,
,
![]() а расстояние между директрисами равно
32.
а расстояние между директрисами равно
32.
Задача 14) Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1. |
1)
|
2)
|
|
3)
|
4)
|
2. |
1)
|
2)
|
|
3)
|
4)
|
3. |
1)
|
2)
|
|
3)
|
4)
|
4. |
1)
|
2)
|
|
3)
|
4)
|
5. |
1)
|
2)
|
|
3)
|
4)
|
6. |
1)
|
2)
|
|
3)
|
4)
|
7. |
1)
|
2)
|
|
3)
|
4)
|
8. |
1)
|
2)
|
|
3)
|
4)
|
9. |
1)
|
2)
|
|
3)
|
4)
|
10. |
1)
|
2)
|
|
3)
|
4)
|
11. |
1)
|
2)
|
|
3)
|
4)
|
12. |
1)
|
2)
|
|
3)
|
4)
|
13. |
1)
|
2)
|
|
3)
|
4) |
14. |
1)
|
2)
|
|
3)
|
4)
|
15. |
1)
|
2)
|
|
3)
|
4)
|
16. |
1)
|
2)
|
|
3)
|
4)
|
17. |
1)
|
2)
|
|
3)
|
4)
|
18. |
1)
|
2)
|
|
3)
|
4)
|
19. |
1)
|
2)
|
|
3)
|
4)
|
20. |
1)
|
2)
|
|
3)
|
4)
|
21. |
1)
|
2)
|
|
3)
|
4)
|
22. |
1)
|
2)
|
|
3)
|
4)
|
23. |
1)
|
2)
|
|
3)
|
4)
|
24. |
1)
|
2)
|
|
3)
|
4)
|
25. |
1)
|
2)
|
|
3)
|
4)
|
Задача
15) Исследовать функцию
![]() на непрерывность: найти точки разрыва
функции и определить их тип. Построить
схематический график функции.
на непрерывность: найти точки разрыва
функции и определить их тип. Построить
схематический график функции.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
|
Задача 16) Найти производные функций.
1. |
1)
|
2)
|
|
3)
|
4)
|
2. |
1)
|
2)
|
|
3)
|
4)
|
3. |
1)
|
2)
|
|
3)
|
4)
|
4. |
1)
|
2)
|
|
3)
|
4)
|
5. |
1)
|
2)
|
|
3)
|
4)
|
6. |
1)
|
2)
|
|
3)
|
4)
|
7. |
1)
|
2)
|
|
3)
|
4)
|
8. |
1)
|
2)
|
|
3)
|
4)
|
9. |
1)
|
2)
|
|
3)
|
4)
|
10. |
1)
|
2)
|
|
3)
|
4)
|
11. |
1)
|
2)
|
|
3)
|
4)
|
12. |
1)
|
2)
|
|
3)
|
4)
|
13. |
1)
|
2)
|
|
3)
|
4)
|
14. |
1)
|
2)
|
|
3)
|
4)
|
15. |
1)
|
2)
|
|
3)
|
4)
|
16. |
1)
|
2)
|
|
3)
|
4)
|
17. |
1)
|
2)
|
|
3)
|
4)
|
18. |
1)
|
2)
|
|
3)
|
4)
|
19. |
1)
|
2)
|
|
3)
|
4)
|
20. |
1)
|
2)
|
|
3)
|
4)
|
21. |
1)
|
2)
|
|
3)
|
4)
|
22. |
1)
|
2)
|
|
3)
|
4)
|
23. |
1)
|
2)
|
|
3)
|
4)
|
24. |
1)
|
2)
|
|
3)
|
4)
|
25. |
1)
|
2)
|
|
3)
|
4)
|
Задача 17) Найти производные функций, заданных параметрически.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
|
Задача 18) Найти производные функций, заданных неявно.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10. |
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
|
Задача 19) Найти предел функции, применяя правило Лопиталя.
1. |
1)
|
2)
|
2. |
1)
|
2)
|
3. |
1)
|
2)
|
4. |
1)
|
2)
|
5. |
1)
|
2)
|
6. |
1)
|
2)
|
7. |
1)
|
2)
|
8. |
1)
|
2)
|
9. |
1)
|
2)
|
10. |
1)
|
2)
|
11. |
1)
|
2)
|
12. |
1)
|
2)
|
13. |
1)
|
2)
|
14. |
1)
|
2)
|
15. |
1) |
2)
|
16. |
1)
|
2)
|
17. |
1)
|
2)
|
18. |
1) |
2)
|
19. |
1)
|
2)
|
20. |
1)
|
2)
|
21. |
1)
|
2)
|
22. |
1)
|
2)
|
23. |
1)
|
2)
|
24. |
1)
|
2)
|
25. |
1)
|
2)
|
Задача
20) Написать уравнение касательной и
нормали к графику функции
в точке
![]()
1.
|
2.
|
3.
|
4.
|
5. |
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
|
Задача 21) Исследовать функции и построить их графики.
1. |
1)
1.
|
2)
|
2. |
1)
|
2)
|
3. |
1)
|
2)
|
4. |
1)
|
2)
|
5. |
1)
|
2)
|
6. |
1)
|
2)
|
7. |
1)
|
2)
|
8. |
1)
|
2)
|
9. |
1)
|
2)
|
10. |
1)
|
2)
|
11. |
1)
|
2)
|
12. |
1)
|
2)
|
13. |
1)
|
2)
|
14. |
1)
|
2)
|
15. |
1)
|
2)
|
16. |
1)
|
2)
|
17. |
1)
|
2)
|
18. |
1)
|
2)
|
19. |
1)
|
2)
|
20. |
1)
|
2)
|
21. |
1) . |
2)
|
22. |
1)
|
2)
|
23. |
1) . |
2)
|
24. |
1)
|
2)
|
25. |
1)
|
2)
|
Задача 22) Найти частные производные первого порядка.
1)
![]() .
2)
.
2)![]() .
.
3)
![]() .
4)
.
4)
![]() .
.
5)
![]() .
6)
.
6)
![]() .
.
7)
![]() .
8)
.
8)
 .
.
9)
![]() .
10)
.
10)
![]() .
.
11)
![]() .
12)
.
12)
![]()
13)
![]() .
14)
.
14)
![]() .
.
15)
![]() .
16)
.
16)
![]() .
.
17)
![]() .
18)
.
18)
![]() .
.
19)
![]() .
20)
.
20)
![]() .
.
21)
![]() .
22)
.
22)
![]() .
.
23)
![]() .
24)
.
24)
![]() .
.
25)
![]() .
.
Задача 23) Найти полный дифференциал от заданной функции двух переменных.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
|
Задача 24) Найти частные производные второго порядка.
1)
![]() .
.
2)
![]() .
.
3)
![]() .
.
4)
![]() .
.
5)
![]() .
.
6)
![]() .
.
7)
![]() .
.
8)
![]() .
.
9)
![]() .
.
10)
![]() .
.
11)
![]() .
.
12)
![]() .
.
13)
![]() .
.
14)
![]() .
.
15)
![]() .
.
16)
![]() .
.
17)
![]() .
.
18)
![]() .
.
19)
![]() .
.
20)
![]() .
.
21)
![]() .
.
22)
![]() .
.
23)
![]() .
.
24)
![]() .
.
25)
![]() .
.
Задача 25) Найти экстремумы функции.
1)
![]() .
.
2)![]() .
.
3)
![]() .
.
4)
![]() .
.
5)
![]() .
.
6)
![]() .
.
7)
![]() .
.
8)
![]() .
.
9)
![]() .
.
10)
![]()
11)
![]() .
.
12)
![]() .
.
13)
![]() .
.
14)
![]() .
.
15)
![]() .
.
16)
![]() .
.
17)
![]() .
.
18)
![]() .
.
19)
![]() .
.
20)
![]() .
.
21)
![]() .
.
22)
![]() .
.
23)
![]() .
.
24)
![]() .
.
25)
 .
.














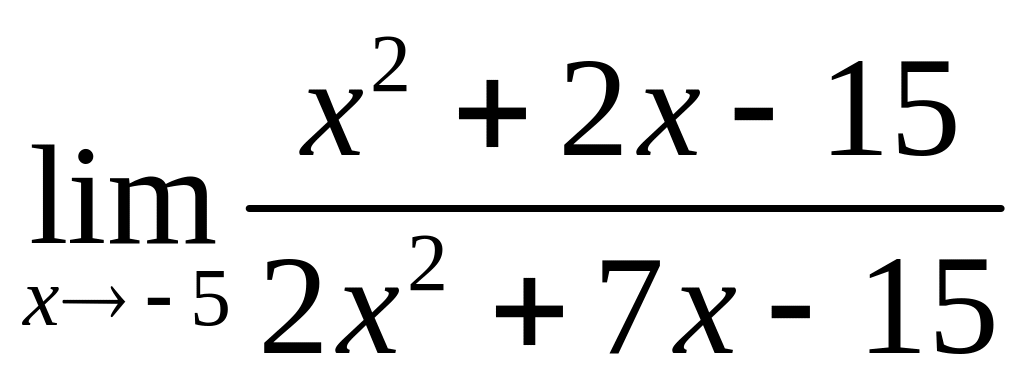































































































 . 2.
. 2.  .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.