5. Дәріс. Функция және оның берілу тәсілдері. Функция шегі. Біржақты шектер. Тамаша шектер. Бірінші тамаша шек. Екінші тамаша шек

Х және У сан жиындары болсын.

1- анықтама. Әрбір санына белгілі ереже немесе заң бойынша сәйкестендірілсе жиынында сан функциясы немесе функция берілген деп атайды f:X Y, X Y бейнелеу X=D(f), Y=E(f) -ты функцияның анықталу облысы, ал -ті функцияның мәндер жиыны деп айтады.

2-анықтама. функциясының графигі деп координаталары x пен болатын жазықтықтағы нүктелер жиынын айтады.

Функцияның берілу тәсілдері:

1. аналитикалық тәсіл,

2. кестелік тәсіл,

3. графиктік тәсіл.

3- анықтама. Егер Х жиынының х₁< x ₂ теңсіздігін қанағаттандыратын кез келген х₁және х₂ нүктелері үшін f(x₁)<f(x₂) (f(x₁)>f(x₂)) теңсіздіктері орындалса, онда f(x) функциясын Х жиынында өспелі (кемімелі) функция деп атайды.

4- анықтама.Егер үшін х₁<x₂ болғанда болса, онда f(x) функциясы Х жиынында кемімейтін (өспейтін) функция деп атайды.

5-анықтама. Өспелі, кемімелі, кемімейтін және өспейтін функцияларды монотонды функциялар деп атайды.

6- анықтама. Егер х₀ нүктесінің кез келген аймағында Х жиынының х₀- ден өзгеше х нүктесі жатса, онда х₀ нүктесін Х жиынының шектік нүктесі деп атайды. Айталық y=f(x) X жиынында анықталсын және х₀ осы Х-тың шектік нүктесі болсын.

Анықтама (Гейне бойынша). Егер х₀ нүктесіне жинақты болатын Х жиынының кез келген тізбегі бойынша құрылған тізбегі санына жинақты болса, онда санын y=f(x) функциясының х₀ нүктесіндегі (немесе дағы) шегі деп атайды. Оны былай жазады:

немесе

Анықтама. (Коши бойынша). Егер сәйкес саны табылып шартты қанағаттандыратын х-тің барлық мәндері үшін теңсіздігі орындалса, онда санын y=f(x) функциясының х₀ нүктесіндегі шегі деп атайды.

7- анықтама. Егер санына сәйкес саны табылып, шарттарын қанағаттандыратын үшін теңсіздігі орындалса, онда функциясы х₀ нүктесінде Коши шартын қанағаттандырады дейді.

Теорема (Коши белгісі). y=f(x)функциясының х₀ нүктесінде тиянақты шегі бар болуы үшін y=f(x) функциясының х₀ нүктесінде Коши шартын қанағаттандыруы қажетті және жеткілікті.

Бірінші тамаша шек

Салдарлар:

1. 2. 3.

Екінші тамаша шек

.

Айталық y=f(x) және z=F(y)функциялары берілсін, онда z=F(f(x)) күрделі функция (супперпозиция) болады.

Теорема. Егер шектер бар болса және үшін болса, онда х₀ нүктесінде күрделі функциясының шегі бар және

= .

8-анықтама. Егер х₀ нүктесінде =0 болса, онда функциясын х₀ нүктесінде шексіз аз деп атайды.

Егер онда пен аздығы ( кішілігі) бірдей ретті дейді; онда , , онда шексіз аз шексіз аз ке қарағанда аздығы к- ретті дейді, оны жазады.

Біржақты шектер ұғымын енгіземіз.

8–анықтама.(Коши бойынша).Егер кез келген > 0 санына сәйкес > 0 x₀<x<x₀₊ ( x₀- <x<x₀) шартты қанағаттандыратын х –тің барлық мәндері үшін теңсіздігі орындалса, онда b санын y=f(x) функциясының x₀ нүктесіндегі оң (сол) жақты шегі деп атайды.

Оны былай жазады:

( )

немесе =f(x₀+0) ( ).

Функцияның оң және сол жақты шектерін функцияның біржақты шектері деп атайды.

Мысалдар:

1. функциясының да шегі бар және ол =6 екенін дәлелдеу керек.

Дәлелдеу:Коши анықтамасын пайдаланамыз. санын аламыз да

болғанда теңсіздігі орындалатынына көз жеткіземіз.

демек демек, онда болады.

2. Барлық нүктелерде анықталған функциясының нүктесінде шегі жоқ екендігін дәлелдеу керек.

Гейне анықтамасы бойынша нольге жинақты болатын екі тізбек алайық:

( =1,2,..)

Осы тізбектерге сәйкес функция мәндерінен екі тізбек құрамыз

=0,

Сонымен

f(x_n)=0, f(x_n¹)=1.

Демек, х=0 нүктесінде f(x)=sin функциясының шегі жоқ.

3. f(x)=хsin функциясының х=0 нүктесіндегі шегі 0 екенін дәлелдеу керек.

болғандықтан онда

6- дәріс. Үзіліссіз функциялар. Больцано- Коши, Вейерштрасс теоремалары.

Айталық f(x) функциясы Х сан жиынында анықталсын.

1. анықтама. Егер f(x) функциясының нүктесінде шегі бар болып, ол f(x) функциясының сол нүктедегі мәні f(x₀)-ге тең болса, онда f(x) функциясын х₀ нүктесінде үзіліссіз деп атайды.

Бұл анықтаманы үзіліссіздіктің формальды анықтамасы дейді.

Функция үзіліссіз болатын нүктені үзіліссіздік нүктесі дейді.

2. анықтама. (Гейне). Егер Х жиынынан алынған кез келген х₁, х₂,...,х_n,.. тізбегі х₀ санына жинақты болғанда осы тізбекке сәйкес келетін f(x₁), f(x₂)…,f(x_n)…тізбегі f(x₀) санына жинақты болса, онда f(x) функциясын х₀ нүктесінде үзіліссіз дейді.

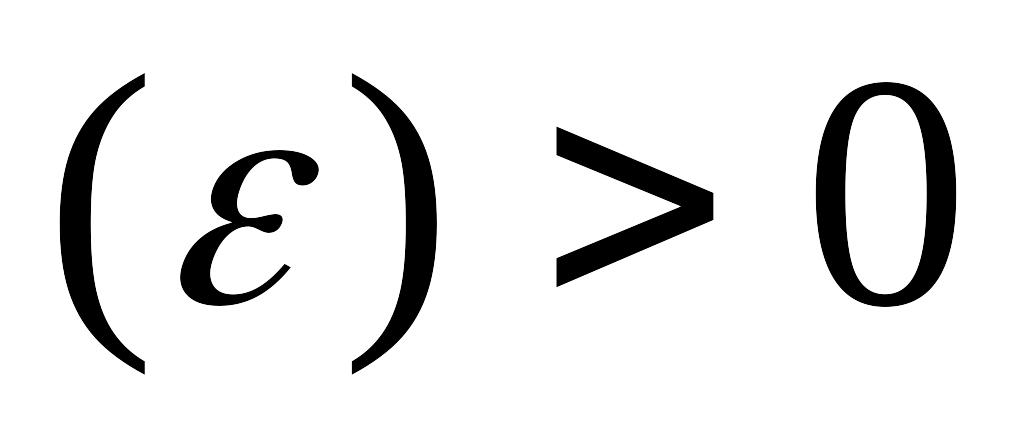3. анықтама. (Коши). Егер кез келген санына сәйкес саны табылып

теңсіздігін қанағаттандыратын х-тің барлық мәндері үшін

теңсіздігі орындалса, онда f(x) функциясын х₀ нүктесінде үзіліссіз деп атайды. Оны жазады.

Енді ал сәйкес келетін функция өсімшесін деп белгілейміз.

4. анықтама. Егер х₀ нүктесіндегі аргументтің шексіз аз өсімшесіне функцияның шексіз аз өсімшесі сәйкес келсе, онда y=f(x) функциясын х₀ нүктесінде үзіліссіз деп атайды да былай жазады:

5-анықтама. Егер y=f(x) функциясы Х сан жиынының әрбір нүктесінде үзіліссіз болса, онда f(x) функциясын Х жиынында үзіліссіз деп атайды.

6- анықтама. Егер х₀ нүктесінде f(x) функциясы үзіліссіз болмаса, онда х₀ нүктесін f(x) функциясының үзіліс нүктесі деп атайды, ал функцияның өзін осы нүктеде үзілісті дейді.

Егер f(x) функциясы х₀ нүктесінде үзіліссіз болса, онда

f(x₀+0) =f(x₀-0)=f(x₀) орындалатыны белгілі.

7- анықтама. Егер f(x₀+0) және f(x₀-0)шекті шектер бар, бірақ ол f(x₀)- ден өзгеше болса, онда х₀ нүктесін бірінші текті үзіліс нүкте деп атайды.

f(x₀+0)-f(x₀-0)- айырмасын f(x) функциясының х₀ нүктесіндегі “секірісі” деп атайды.

Егер болса, онда х₀ нүктесін жойылатын үзіліс нүкте деп атайды.

8- анықтама. Егер оң немесе сол жақты шектердің жоқ дегенде біреуі болмаса, онда х₀ нүктесін f(x) функциясының екінші текті үзіліс нүктесі дейді.

Больцано- Кошидің бірінші теоремасы.

f(x) функциясы кесіндісінде үзіліссіз және кесіндінің ұштарында функция мәндерінің таңбалары әр түрлі болса, онда аралығында ең болмаса бір нүкте табылып, f(c)=0 болады.

Больцано- Кошидің екінші теоремасы.

Егер f(x) функциясы кесіндісінде үзіліссіз және болса, онда функция осы сегментте мен сандарының арасында жатқан кез келген мәнін қабылдайды, демек теңдігін қанағаттандыратын кемінде бір с саны табылады.

Вейерштрасстың 1-теоремасы.

кесіндісінде үзіліссіз f(x) функциясы осы кесіндіде шектелген.

Вейерштрасстың 2-теоремасы. Егер функциясы кесіндісінде үзіліссіз болса, онда осы сегментте функция өзінің дәл төменгі және дәл жоғарғы шекараларын қабылдайды, демек х₁, х₂, нүктелер табылып

Қайсыбір тамаша шектер:

1. 2.

3. 4.

8. дәріс. Бір айнымалыдан тәуелді функциялардың дифференциалдық есептеуі. Туынды ұғымы, дифференциалдау ережелері. Күрделі және параметрлік түрде берілген функциялардың туындысы. Кері функциялардың туындысы. Туынды кестесі.

1- анықтама. функциясы қайсыбір нүктесінің аймағында анықталсын нүктесіндегі аргумент өсімшесі , ал сәйкес функция өсімшесі және - шекті шек бар болсын. Онда оны функциясының нүктесіндегі туындысы деп атайды:

Туындыны анықтауды функцияны дифференциалдау деп атайды. нүктесінде шекті туындысы бар функцияны дифференциалданатын функция деп атайды.

1-теорема. Егер , функциалары х нүктесінде дифференциалданатын болса, онда осы нүктеде ; және дифференциалданады және

1.

2.

3.

Күрделі функцияның туындысы.

2-теорема. Егер пен функциялары сәйкес және нүктелерінде дифференциалданатын болса, онда күрделі функция нүктесінде дифференциалданады және .

Кері функцияның туындысы.

3- теорема. Егер функциясы аралығында үзіліссіз, өспелі (кемімелі) және қандай да бір нүктесінде болса, онда кері функциясының осы нүктеде туындысы бар және ол немесе анықталады.

Енді у- тің х-ке тәуелділігі параметрлік түрде берілсін

4- теорема. Егер , дифференциалданатын болса және онда функциясы х нүктесінде дифференциалданады және

Туынды кестесі

1. .

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

Мысалдар. Туынды анықтамасы бойынша туындыларын анықтау керек:

1. сондықтан

2. онда

.

3.

4. дәл осылай дәлелденеді:

5.

6. және

дәлелдейік.

Дәл осылай

7.

8. табыңдар.