3. Фокустары -те жататын және олардың қашықтқы 10-қа тең, осі бойынша ұзындықы 8-ге тең гиперболаның канондық теңдеуін жаз.
Шешуі:
Есептң
шарты бойынша
іздеп отырқан теңдеуіміз
4. Параболаның теңдеуі берілген
Р
параметрі мен төбесінң координатасын
табу керек.
Шешуі:
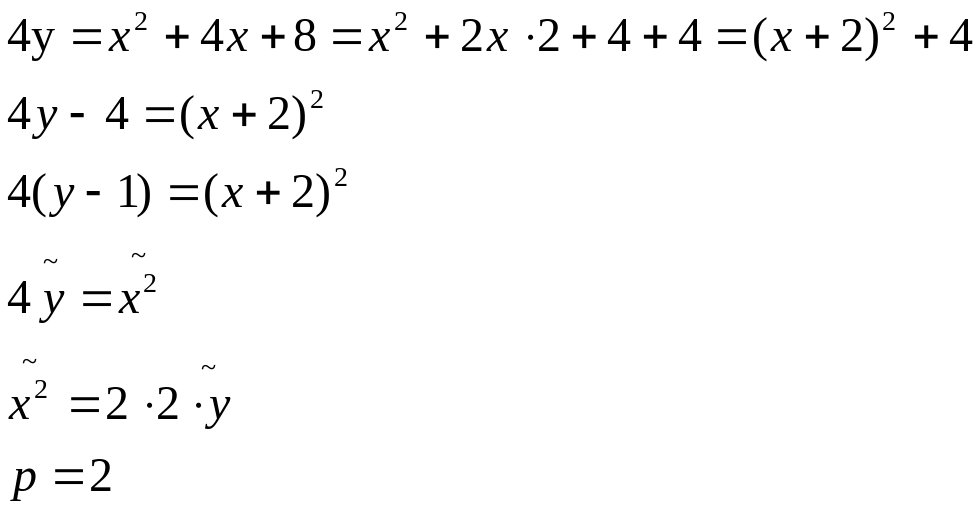
төбесі (-2,1)
3. Ү.Ж.: [14], №№ 2.234, 2.236, 2.247, 2.266, 2.286, 2.300, 2.329, 3.345, 2.349, 2.357, 2.363, 2.369, 2.373, 2.390.
4. Тексеру сұрақтары
1 Параболаның канондық теңдеуі. Директриса деген не?
2. Нүктелердң геометриялық орны арқылы эллипсті анықтау.
№ 29-30 жаттығу сабағы. Екінші ретті беттер.
А.Ж.: [14], 2.348, 2.356, 2.362, 2.368, 2.372, 2.389.
Есептердің шешу үлгілері
1.
Мына теңдеу қай бетті анықтайды
,
схемалық чертеж салу керек
.
Шешуі.
Бұл теңдеуде
айнымалысы жоқ демек, бұл бет цилиндр,
осіне параллель. Бақыттаушының теңдеуі
мына түрде берілген.
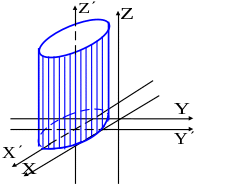
2. Мына теңдеумен берілген беттң түрін анықта. Схемалық сызба жаса .
Шешуі.
.
немесе
эллиптикалық
цилиндр
3. Бір қуысты гиперболоидті қима әдісімен зертте
жазықтықтар
Шешуі
-
эллипс жарты осьтермен
.
-
эллипс жарты
осьтермен
-
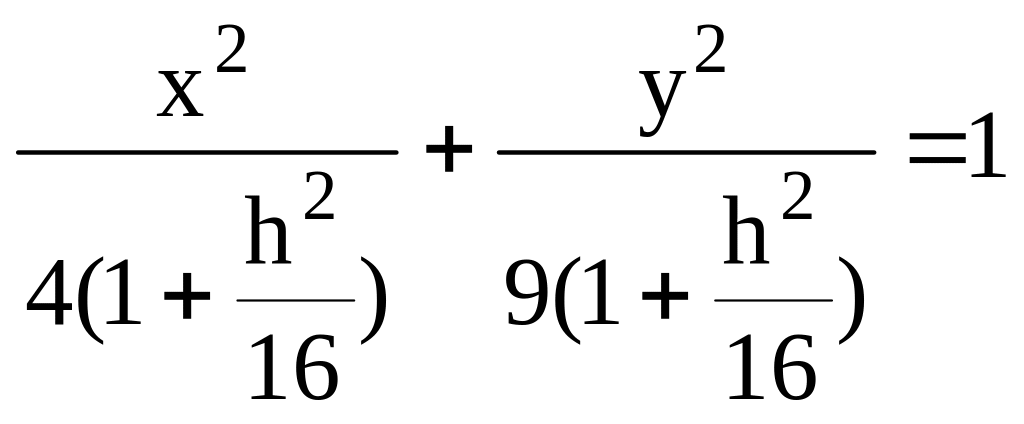эллипс жарты
осьтермен
-
эллипс жарты
осьтермен
.
Сөйтіп,
өзгеруімен
-тен
қимадан
эллипс
аламыз..
Егер
бетті
және
жазықтықтарымен қисақ,
онда гипербола қимасын аламыз.
гипербола,
гипербола
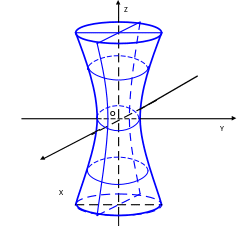
4. Координаталар жүйесіне байланысты беттң формасы мен орналасуын зертте
Шешуі.
Қима
әдісін қолданамыз.
жазықтықымен қиямыз, мынандай эллипс
аламыз
болсын.
Онда
парабола
төбелері
Егер
,
онда
парабола.
Z
O
Y
3
X
5. Қандай бет мына теңдеумен анықталады
Шешуі.
және
мүшелері бойынша топтаймыз:
.
нүктелері
бойынша параллель көшіреміз.
Мынандай
беттң теідеуін аламыз.
Бұл екі қуысты гиперболоид
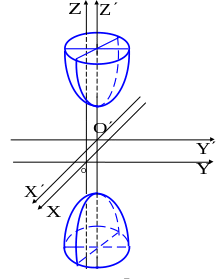
6. Қандай бет мына теңдеумен анықталады
.
Шешуі.
және
бойынша
топтаймыз.
.
,
.
,
бұл - гиперболалық параболоид
3. Ү.Ж.: [14], №№ 2.349, 2.357, 2.363, 2.369, 2.373, 2.390.
4. Тексеру сұрақтары
1. Қима әдісі нені білдіреді?
2. Қандай бет цилиндрлік деп аталады?
Студенттің өзіндік жұмыстарына арналған материалдар
Курс бойынша жазбаша жұмыстың тақырыптары.
Бақылау жұмыстарының тақырыптары
1. Сызықты алгебра
2. Векторлық алгебра
Ұсынылатын ңдебиет: Рябушко А.П., Бархатов В.В. және т.б. «Индивидуальные задания по высшей математике», бөлім 1,2