Построение двумерных температурных полей.

Рассмотрим два метода, которые могут быть сравнительно просто использованы в инженерной практике для расчета двумерных температурных полей конструкций.

Метод сеток.

Область двумерного сечения конструкции, для которой требуется пост-

роить температурное поле, делят на элементарные площадки, центры которых соединяют сосредоточенными термическими сопротивлениями (рис. а). Таким образом, переходят от поля к тепловой сетке (рис. б) с сосредоточенными параметрами.

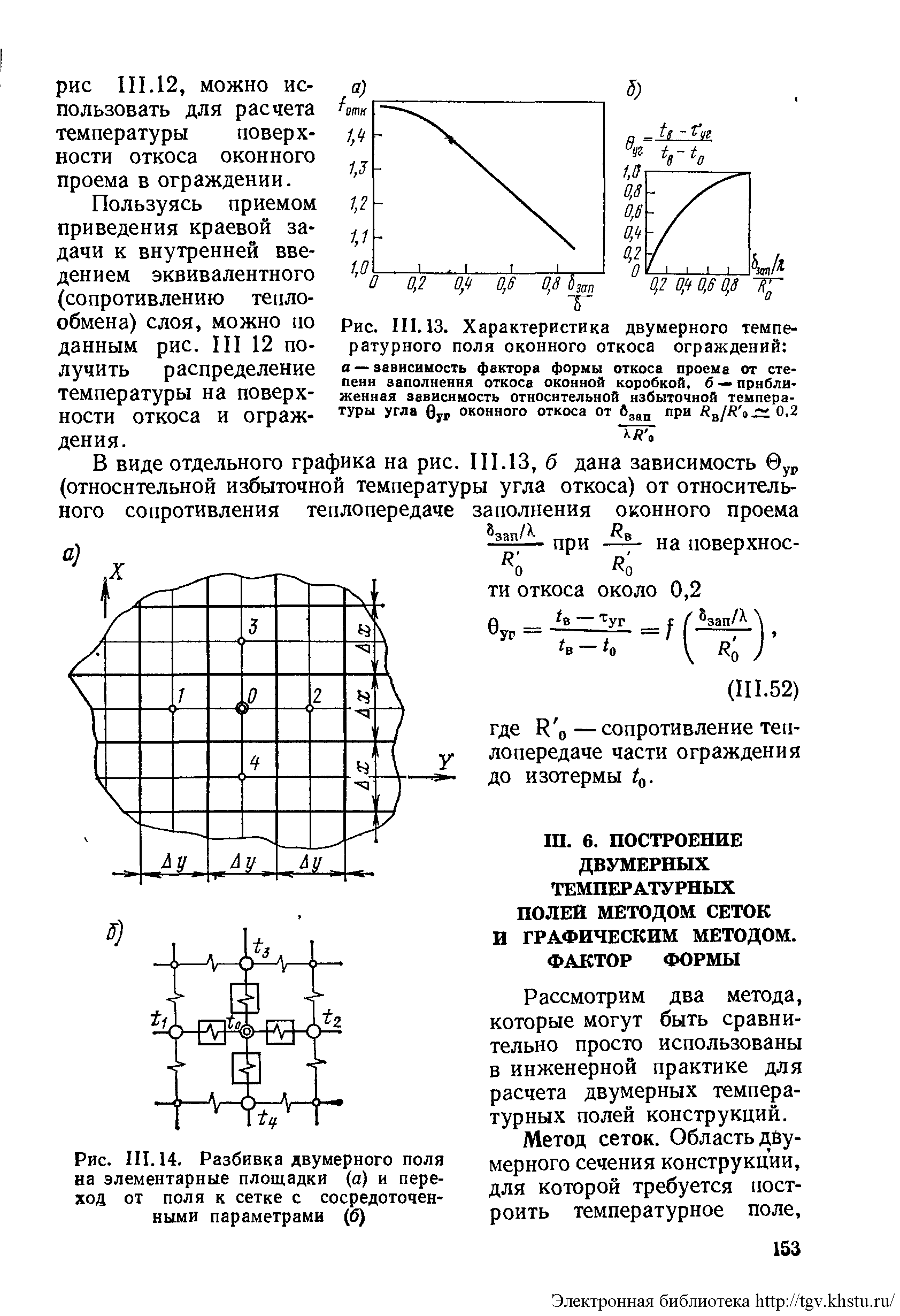
Уравнение стационарной теплопроводности для такой сетки (поле однородное) в конечных разностях имеет вид

Вторые конечные разности приращения температуры равны:

Решение уравнения относительно температуры в произвольном узле сетки, если шаг сетки одинаковый, может быть получено в виде

Таким образом, при однородном поле температура в произвольном узле сетки равна среднеарифметическому значению температуры в соседних узлах.

Для конструкции неоднородной и с произвольным шагом разбивки сетки решение конечноразностного уравнения относительно to имеет вид

где - показатели проводимости соединений тепловой сетки

между соответствующими узлами в центрах элементарных площадок.

Из уравнения следует, что в общем случае температура в произвольном узле равна средневзвешенному (по проводимостям связей) значению температур в соседних узлах. Это общее уравнение может быть использовано, в том числе для определения температуры в узлах, граничащих с поверхностью ограждения, а также в узлах на стыках материальных слоев.

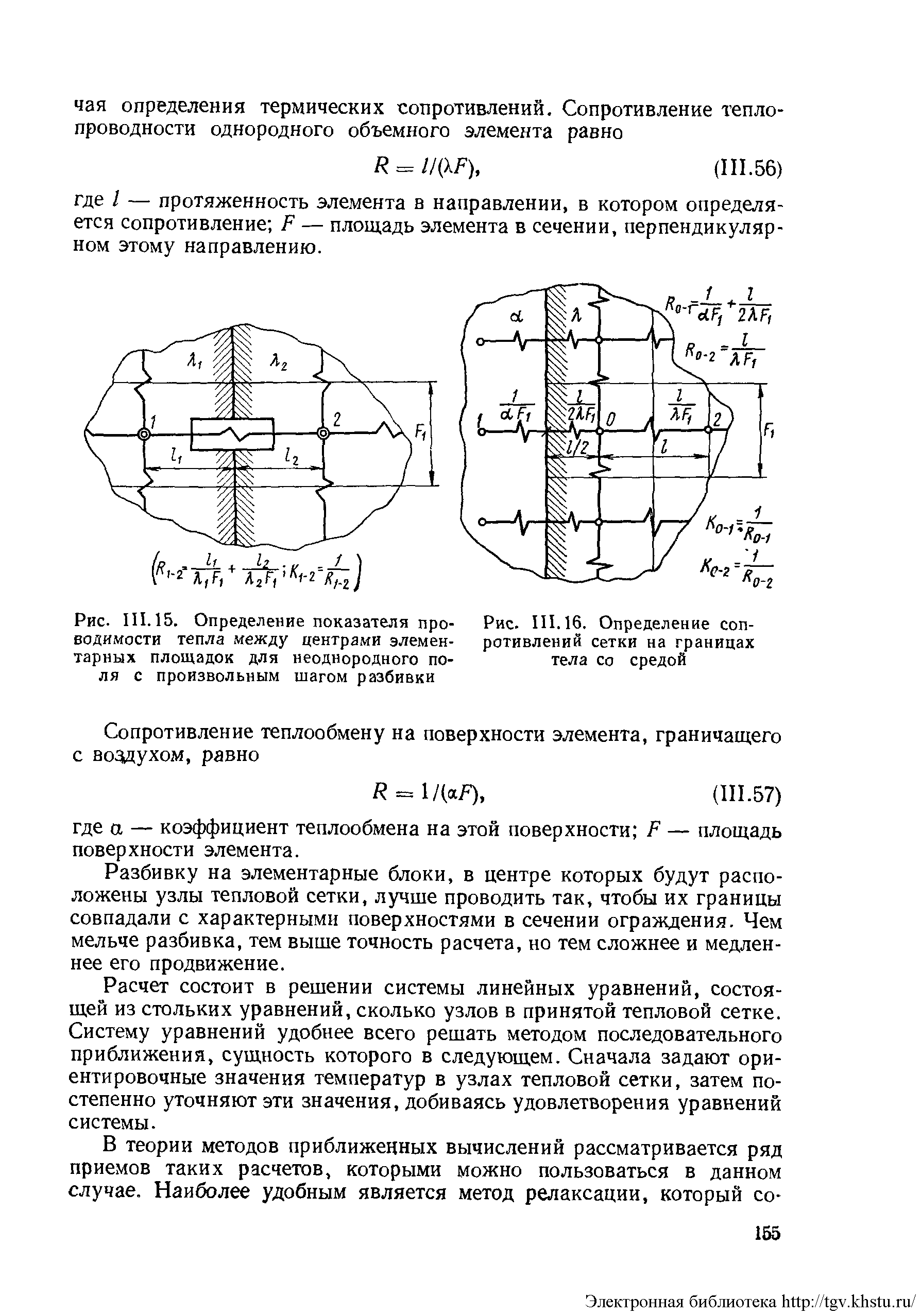
Показатель проводимости К между узлами должен определяться по правилу сложения параллельно и последовательно расположенных термических сопротивлений. Может быть два случая определения термических сопротивлений. Сопротивление теплопроводности однородного объемного элемента равно

где 1-протяженность элемента в направлении, в котором определяется сопротивление; F - площадь элемента в сечении, перпендикулярном этому направлению.

Сопротивление теплообмену на поверхности элемента, граничащего

с воздухом, равно

где α- коэффициент теплообмена на этой поверхности; F - площадь поверхности элемента.

Расчет состоит в решении системы линейных уравнений, состоящей из стольких уравнений, сколько узлов в принятой тепловой сетке. Систему уравнений удобнее всего решать методом последовательного приближения, сущность которого в следующем. Сначала задают ориентировочные значения температур в узлах тепловой сетки, затем постепенно уточняют эти значения, добиваясь удовлетворения уравнений системы.

Наиболее удобным является метод релаксации, который состоит в определении дебаланса в каждой точке, с постепенным его уменьшением и доведением до величин, близких к нулю, изменением температуры в данной и соседних точках.

Для простейшего случая однородной конструкции дебаланс в узле Δt можно записать в виде

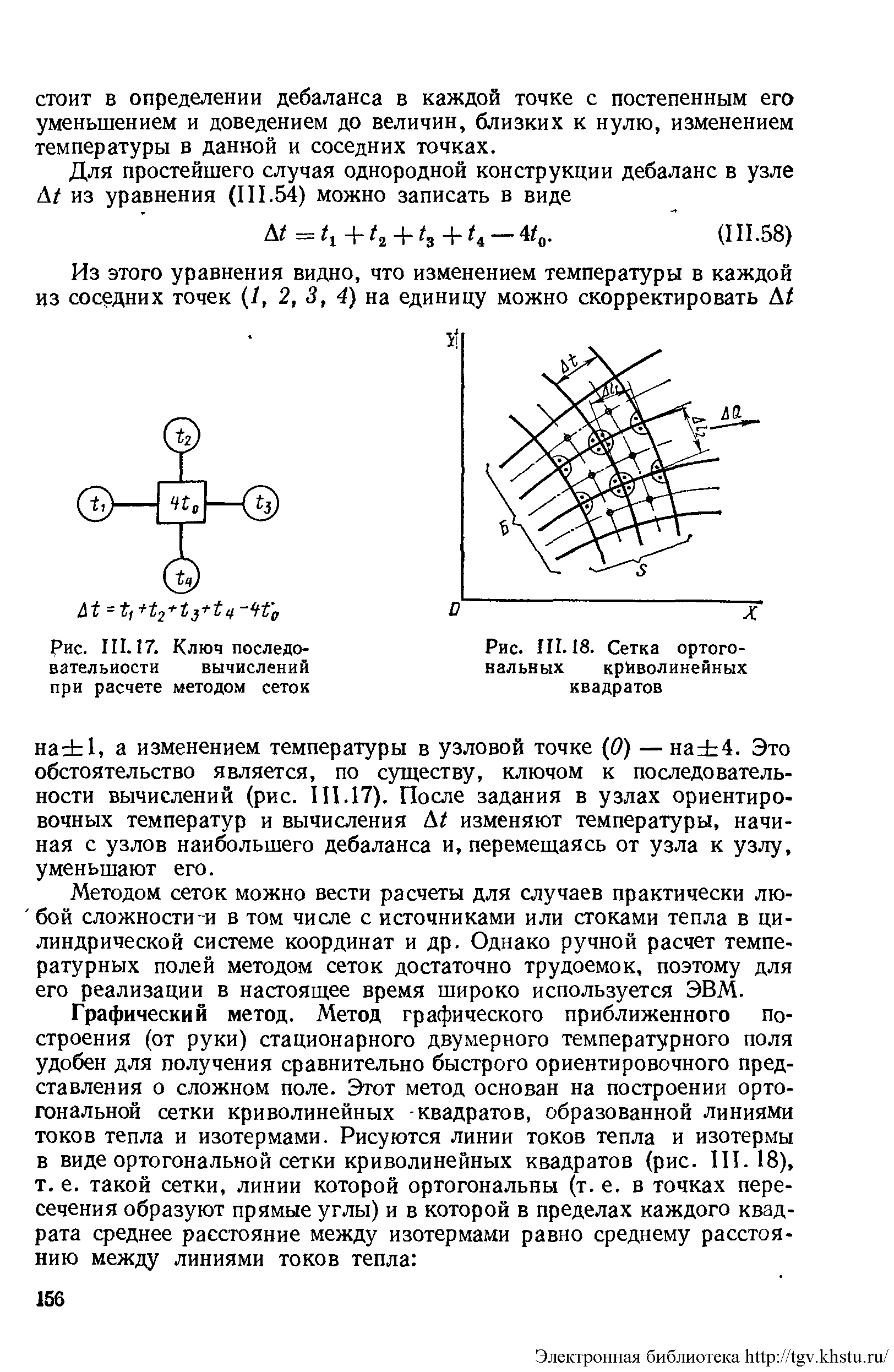
Из этого уравнения видно, что изменением температуры в каждой из соседних точек (1, 2, 3, 4) на единицу можно скорректировать Δt на + -1, а изменением температуры в узловой точке (О) на +- 4. Это обстоятельство является, по существу, ключом к последовательности вычислений. После задания в узлах ориентировочных температур и вычисления Δt изменяют температуры, начиная с узлов наибольшего дебаланса и, перемещаясь от узла к узлу, уменьшают его.

Графический метод.

Метод графического приближенного построения стационарного двумерного температурного поля удобен для получения сравнительно быстрого ориентировочного представления о сложном поле. Этот метод основан на построении ортогональной сетки криволинейных квадратов, образованной линиями токов тепла и изотермами. Рисуются линии токов тепла и изотермы в виде ортогональной сетки криволинейных квадратов (рис.), т. е. такой сетки, линии которой ортогональны и в которой в пределах каждого квадрата среднее расстояние между изотермами равно среднему расстоянию между линиями токов тепла:

В такой сетке поток тепла в «трубке», образованной двумя линиями тока, равен

или ,

где Δt- перепад температур между соседними изотермами, равный

τ1 и τ1- температуры на границах области, для которой строится температурное поле; S - число интервалов между изотермами.

Если число трубок тока (интервалов между линиями тепловых потоков) в пределах рассматриваемой области (части конструкции) обозначить через Б, то общее количество тепла, проходящее через эту часть конструкции, будет равно

а сопротивление теплопроводности этой части

Фактор формы

Отношение Б/S в формуле является геометрическим параметром, характеризующим область (двумерного температурного поля) определенной конфигурации. Для одномерного поля стенки с шириной поверхности в один калибр (один калибр равен толщине стены) Б/S == 1, а шириной поверхности в два калибра равно 2 и т. д. Для двумерной области с такой же шириной поверхности эти отношения другие. Отношение геометрических параметров для двумерной и одномерной областей одинаковой ширины показывает, во сколько раз изменяется тепловой поток через поверхность определенной ширины в двумерной области по сравнению с одномерной.

Обычно угол, стык, откос, включение и другие изменения в одномерной конструкции вызывают нарушение одномерности температурного поля на расстоянии до двух калибров по ширине ограждения, поэтому для всех случаев двумерных полей в ограждении необходимо учитывать участок ограждения шириной в два калибра. За один калибр для реальных ограждений (многослойных, имеющих конечные значения сопротивлений теплообмена) принимают условную толщину однородного ограждения с сопротивлением теплопроводности Ro и коэффициентом теплопроводности теплоизоляционного материала λ. Ширина аf, в два калибра равна

При расчете передачи тепла через двумерные элементы в ограждении (участки конструкций с двумерным температурным полем) удобно пользоваться так называемым фактором формы. Фактором формы f двумерногo элемента ограждения называется отношение гeoметрических параметров Б/S двумерной и одномерной частей ограждения при их одинаковой ширине по поверхности, равной двум калибрам:

где Б/S - отношение числа трубок тока к числу изотермических полос (интервалов между изотермами) в ортогональной сетке криволинейных квадратов, расположенных в области двумерного температурного поля на ширине поверхности в два калибра;

Фактор формы показывает, во сколько раз больше проводимость тепла двумерным элементом по сравнению с одномерным. Или при одинаковой разности температур и прочих условиях он показывает, во сколько раз больше теряется тепла через двумерный элемент ограждения по сравнению с теплопотерями через его гладь.

В расчете потерь тепла помещением площади ограждений принимают по наружному обмеру; в этом случае f следует определять по наружной поверхности.

Теплопередача через ограждение с теплопроводным включением.

Распространенным случаем двумерного температурного поля является конструкция с теплопроводным включением. Наиболее простым является случай, когда ребро из теплопроводного материала частично или полностью прорезает малотеплопроводную толщу основной конструкции.

При рассмотрении конструкции с теплопроводным включением инженера интересуют два вопроса: какая будет наинизшая температура на внутренней поверхности ограждения в зоне включения и какие будут теплопотери через эту зону.

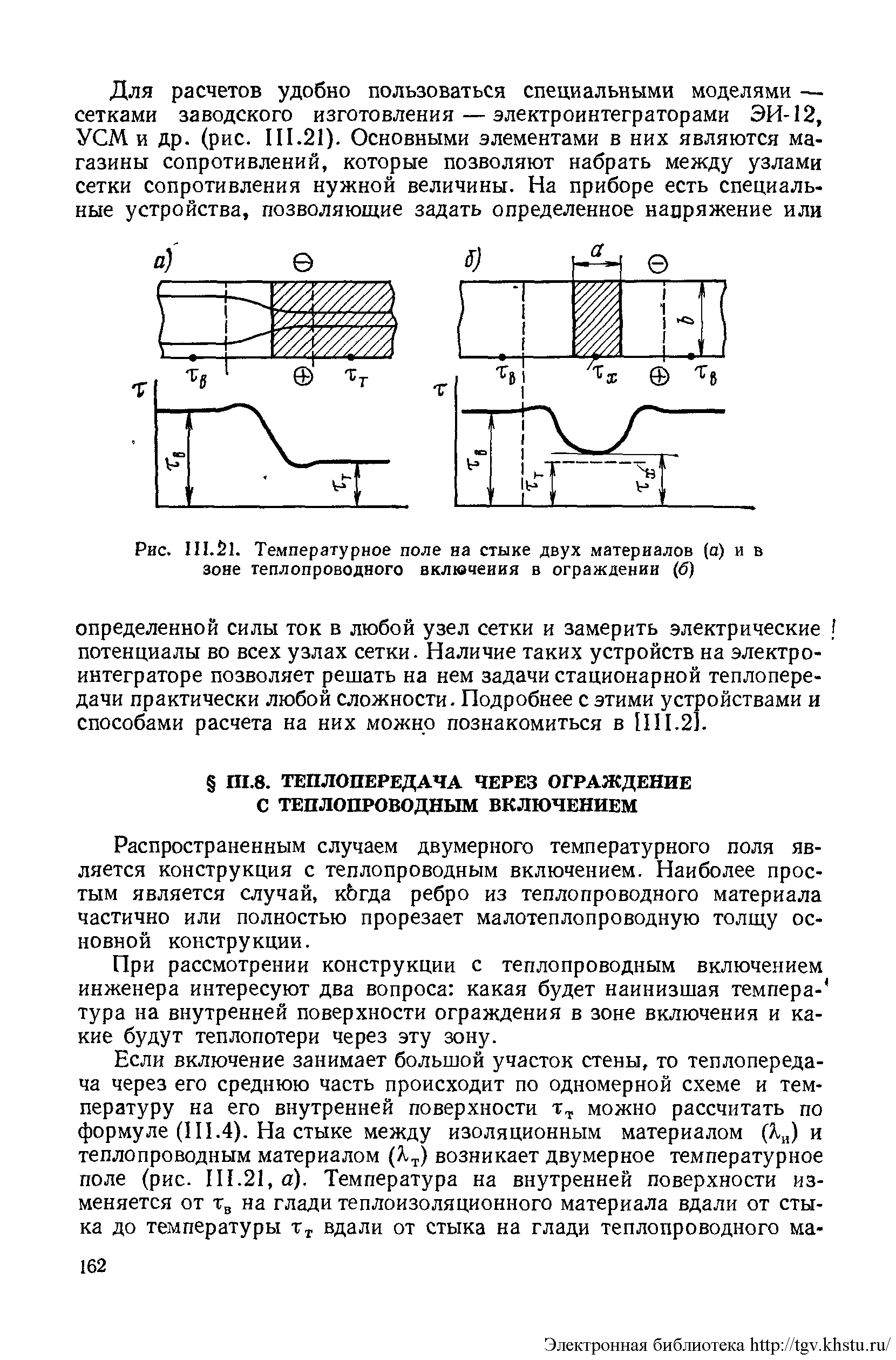
На стыке между изоляционным материалом (λ_и) и теплопроводным материалом (λ_т ) возникает двумерное температурное поле (рис. а). Температура на внутренней поверхности изменяется от τ_в на глади теплоизоляционного материала вдали от стыка до температуры τ_т вдали от стыка на глади теплопроводного материала. Заметное влияние стыка распространяется на расстояние одного -двух калибров и более.

При большой ширине включения а> 2b температура τх в его средней части близка к τ_т, При меньших размерах температура τ_х будет отличаться от τ_{в и} τ_т (рис. б).

Удобно пользоваться показателем относительной избыточной температуры

Он показывает, на какую долю от перепада τ_в - τ_т понизилась температура

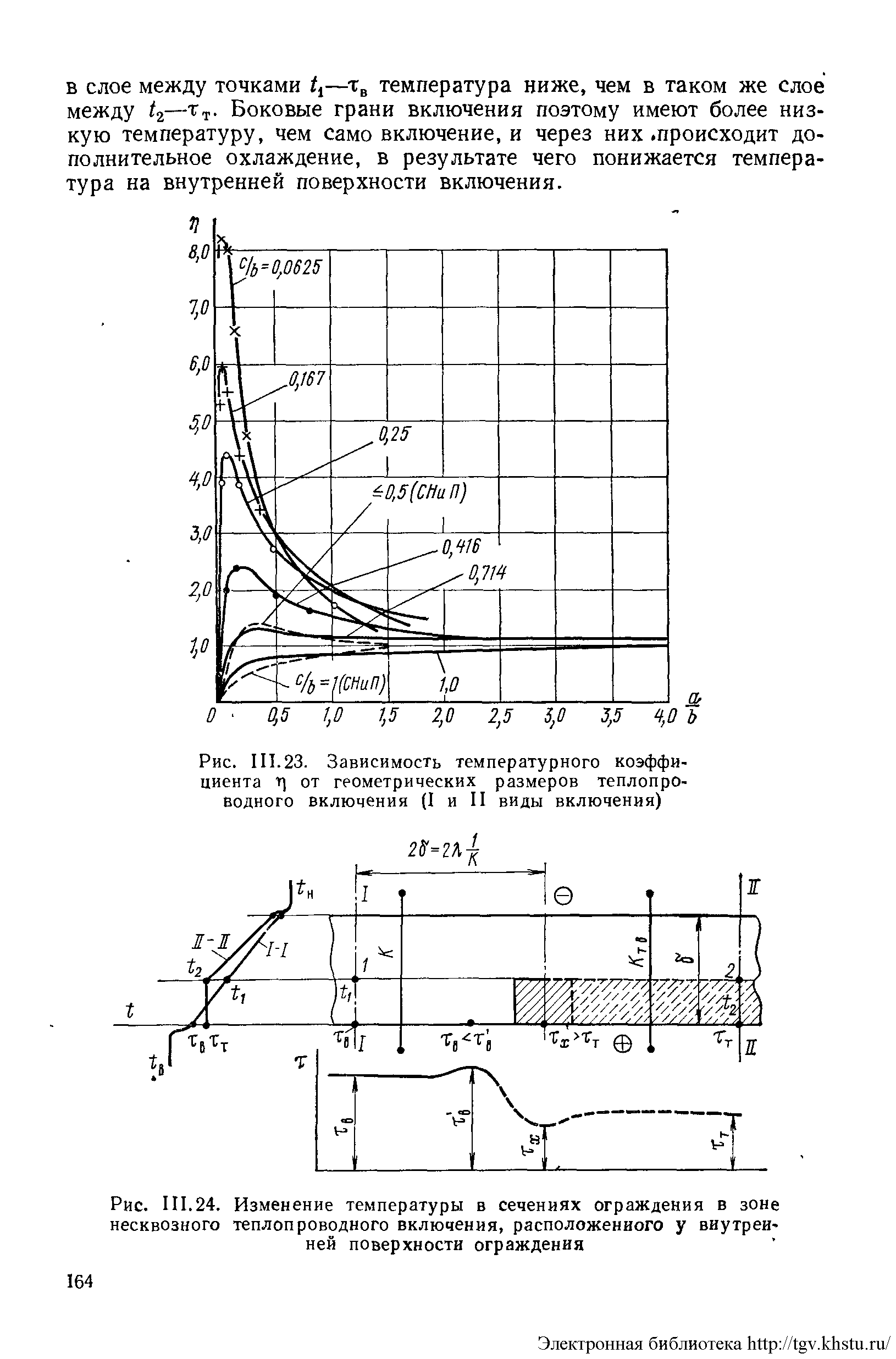
τ_х в середине включения относительно τ_в. Величина η зависит от сопротивлений толщи стены и включения, от сопротивлений тепловосприятию и тепло-

отдаче, но в основном она определяется геометрическими соотношениями а/b и с/b (рис.).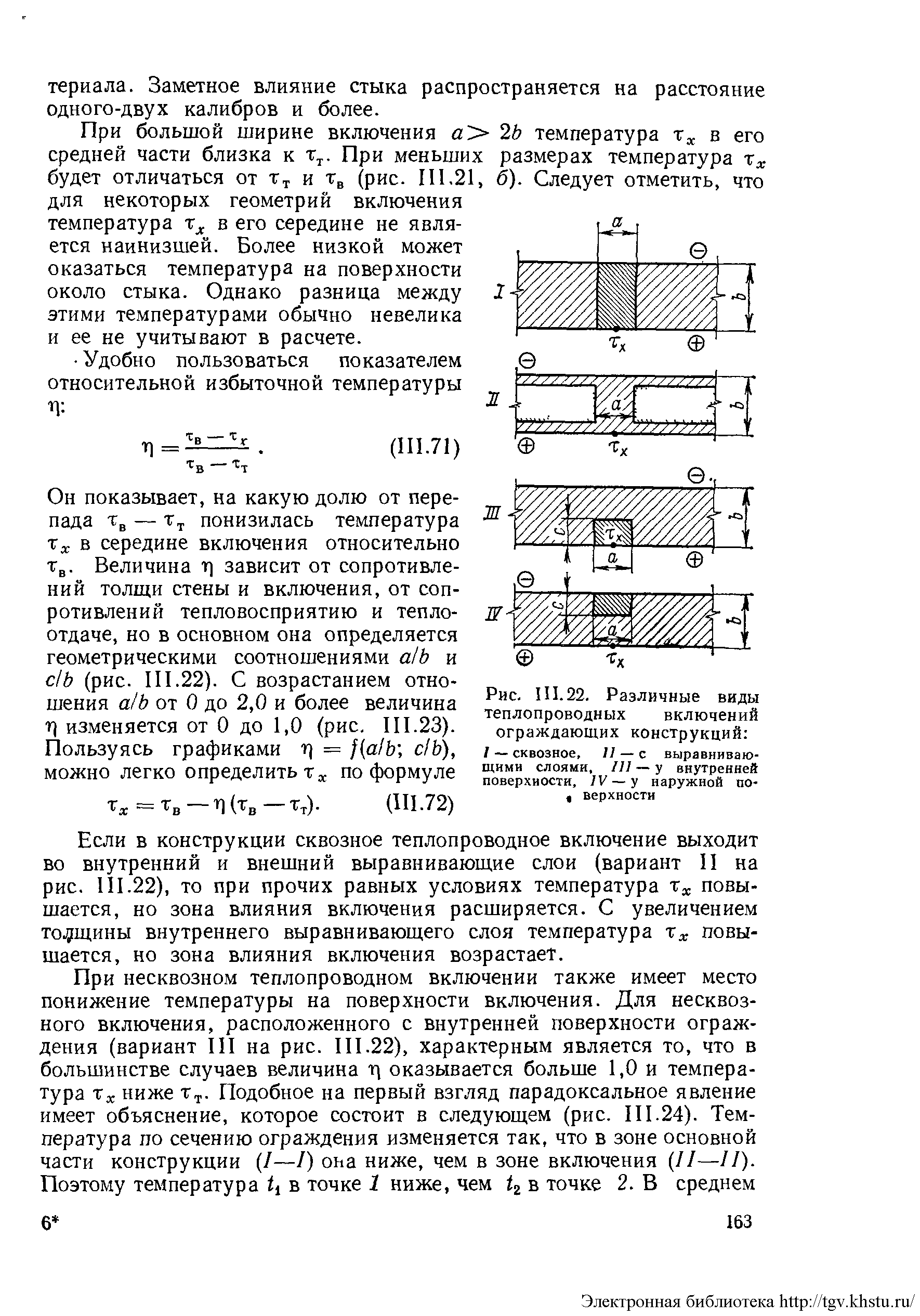

Определим фактор формы теплопроводного включения fвкл для этого рассмотрим на рисунке часть конструкции шириной в два калибра в каждую сторону от оси симметрии включения.

При этом будем предполагать отсутствие тепловых потоков через торцевые поверхности включения.

Пользуясь правилом сложения проводимостей, определим проводимость Квкл части конструкции шириной в два калибра от оси включения:

где К и Кт.в - коэффициенты теплопередачи, рассчитанные соответственно по сечению основной конструкции ограждения и по сечению теплопроводного включения.

Такая же площадь в два калибра глади основной конструкции ограждения имеет проводимость

Фактор формы равен отношению этих проводимостей:

Если конструкция ограждения имеет теплопроводные включения в виде ряда подобных элементов, которые расположены на небольшом расстоянии друг от друга, то целесообразно для расчета теплопотерь определить условное сопротивление теплопередаче всей конструкции.

Теплопередача в наружном углу.

Для наружного угла фактор формы fуг равен

Он показывает, что в пределах расстояния, равного двум калибрам от наружного угла по внешней поверхности, количество теряемого тепла на 32% меньше, чем теряется через такую же площадь на глади стены.

Фактор формы для наружного угла, определенный для ширины в два калибра по внутренней поверхности ограждения, равен 1,18. Это значит, что потери тепла через внутреннюю поверхность наружного угла такой ширины больше, чем через гладь, стены, на 18 %.

Теплопотери 1 м наружного угла однородного ограждения шириной в два калибра (2λRo) с учетом фактора формы равны

Дополнительные потери тепла через угол по сравнению с теплопотерями через одномерную стену равны

Температуру в углу τyг в диапазоне Ro от 0,5 до 2,5 можно рассчитать по приближенной формуле:

Теплопередача стыка ограждений.

Для приближенного определения температуры tст в углу на стыке внутренних поверхностей можно воспользоваться графиками виде зависимости относительной избыточной температуры:

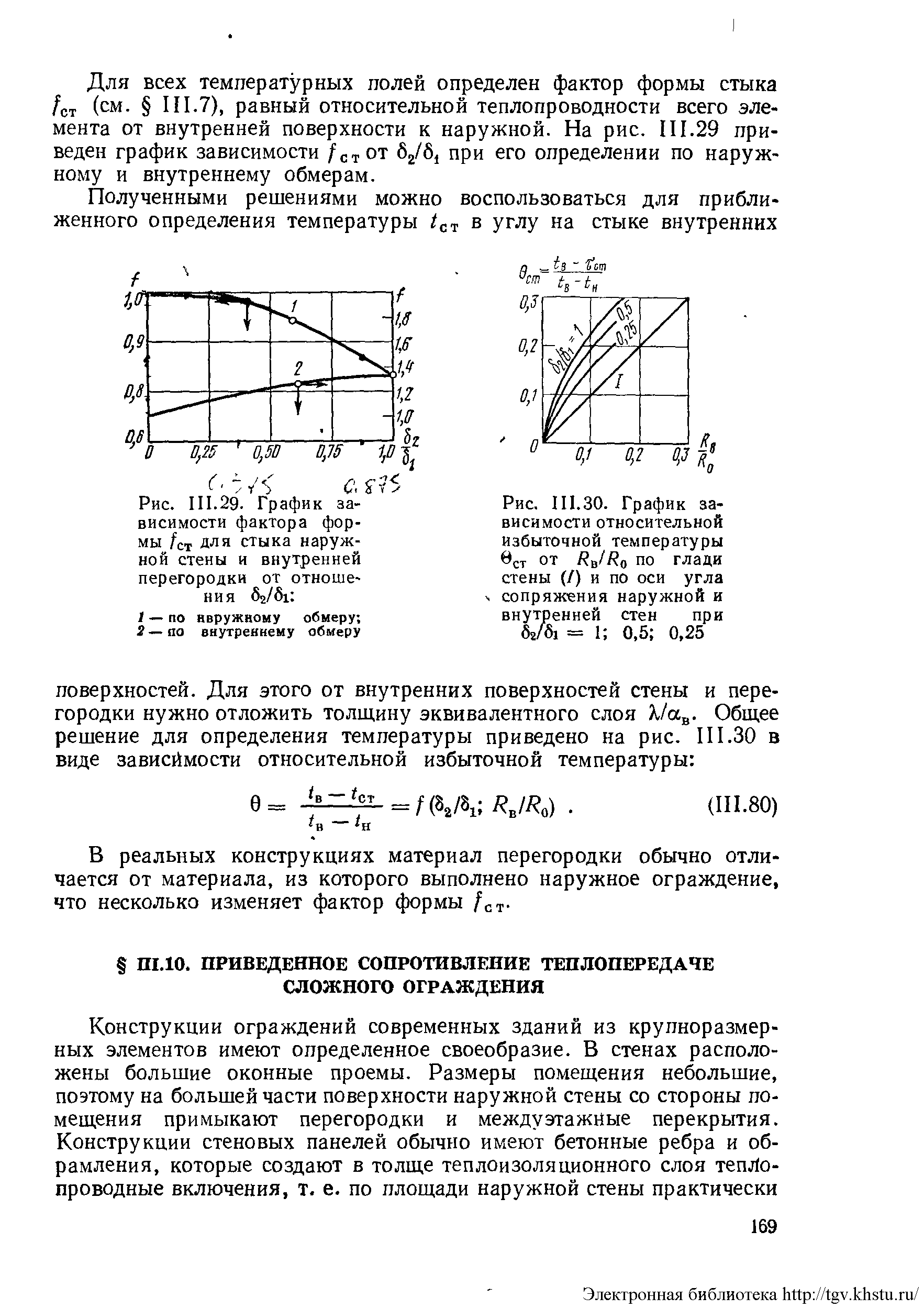
В реальных конструкциях материал перегородки обычно отличается от материала, из которого выполнено наружное ограждение, что несколько изменяет фактор формы fст.