Обеспеченность летних внутренних условий.
Выбор расчетных внутренних условий для летнего периода года имеет специфичность. Он должен проводиться с учетом следующих факторов: 1) назначения здания и помещения; 2) климата географического района строительства; 3) не стационарности летних условий;4) градаций уровней требований и способа обеспечения заданных условий; 5) выполняемой человеком работы и степени ее физической тяжести; 6) наличия больших нагретых или охлажденных поверхностей; 7) длительности пребывания людей; 8) требования обеспеченности расчетных условий.
За основу определения внутренних условий удобно принять условия для наиболее распространенного случая основных помещений жилых и общественных зданий, расположенных в умеренном климате, с учетом не стационарности условий, для двух уровней требований при их обеспечении средствами вентиляции и кондиционирования воздуха.
Летом, так же как и зимой необходимо определять требуемую обеспеченность поддержания заданных внутренних условий. Для летних условий особенно необходимо задавать коэффициент обеспеченности и по числу n случаев (Коб, n) и по продолжительности (Δz) отклонений (Коб, Δz). Коэффициент обеспеченности по числу случаев равен
а по продолжительности отклонений
где N и Z - соответственно общее число случаев и общая продолжительность во времени для принятого сезонного периода года; n и Δz- соответственно число случаев и продолжительность отклонения условий от расчетных.
Обеспеченность поддержания условий в помещении зависит от теплозащиты ограждающих конструкций, тепловой и холодильной мощности систем обеспечения микроклимата, которые выбираются по расчетным наружным условиям. Поэтому требование обеспеченности расчетных внутренних условий должно учитываться при выборе расчетных характеристик наружного климата.
В действующих нормах приняты три градации климата (А, Б и В) для расчета систем обеспечения микроклимата. Их приближенно можно определить коэффициентами обеспеченности.
В таблице приведены рекомендуемые градации обеспеченности расчетных внутренних условий для летнего периода и их связь с данными СНиПа.
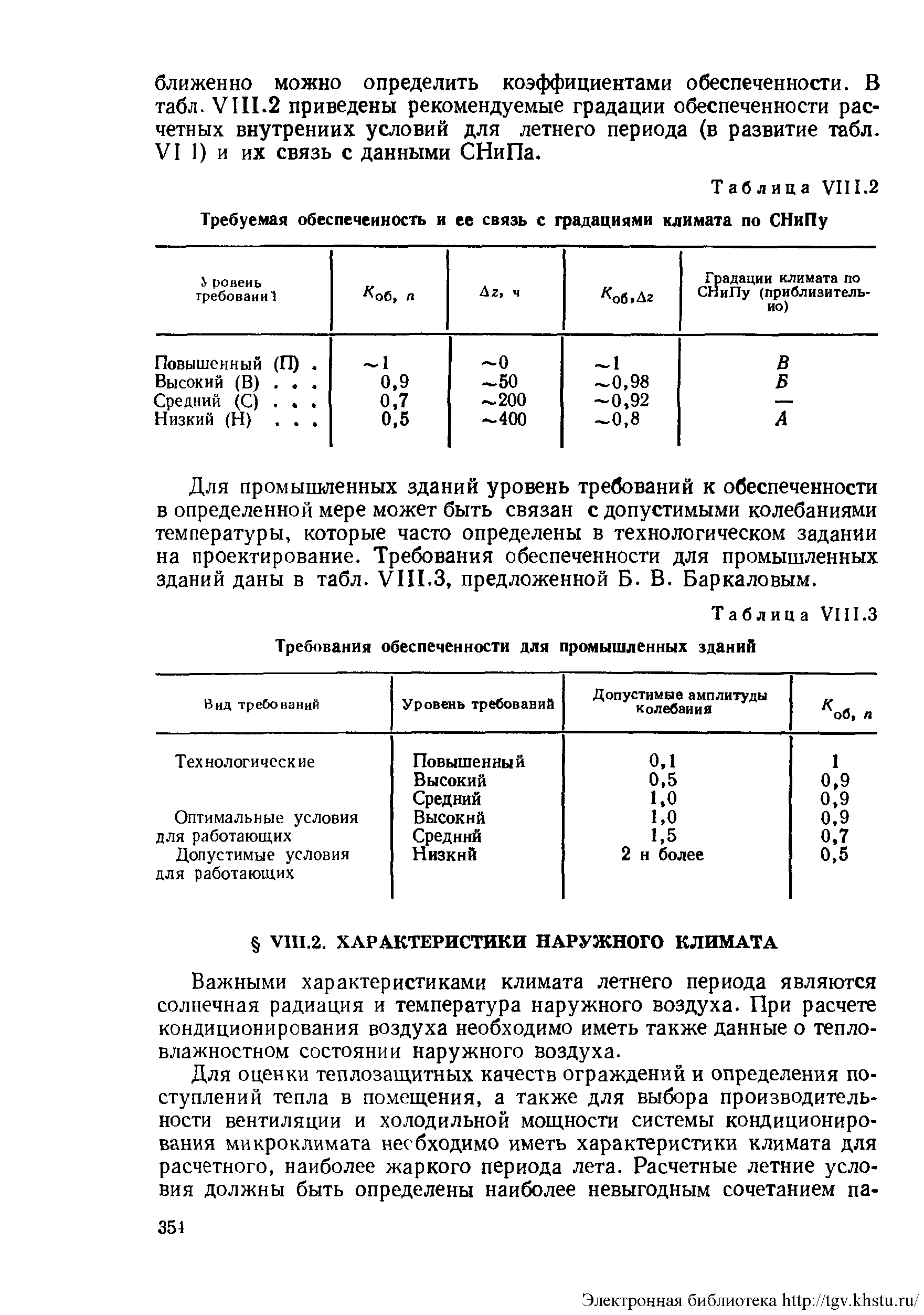
Для промышленных зданий уровень требований к обеспеченности
в определенной мере может быть связан с допустимыми колебаниями
температуры, которые часто определены в технологическом задании
на проектирование. Требования обеспеченности для промышленных
зданий даны в таблице.
Стационарная теплопередача через ограждающие конструкции
Процесс передачи тепла через ограждение, все параметры которого остаются неизменными во времени, называется стационарным и является наиболее простым случаем теплопередачи. К стационарной теплопередаче обычно стремятся привести важные для проектирования ограждений и систем расчетные условия.
Одномерное температурное поле
Простейшим является одномерное стационарное температурное поле, которое для многослойного ограждения может быть определено дифференциальным уравнением
Если линейный масштаб сечения ограждения заменить масштабом термических Сопротивлений R =х/λ, то уравнение можно переписать в виде
В общем случае ограждение состоит из конструктивного (несущего) слоя, теплоизоляционного слоя, а также паро- или гидроизоляционного слоя, внутреннего и внешнего фактурных слоев. В отношении режима теплопередачи основными являются конструктивный и теплоизоляционный слои.
Теплоизоляционный слой может быть расположен с внутренней и внешней сторон ограждения. Следует иметь в виду, что с теплотехнической точки зрения выгоднее располагать теплоизоляционный слой с внешней стороны ограждения, так как в этом случае при прочих равных условиях имеются следующие достоинства:
1) отсутствует возможность выпадения конденсата и накопления жидкой влаги в толще конструкции, а поэтому не требуется устройства дополнительной пароизоляции с внутренней поверхности ограждения;
2) стык между материальными слоями находится при положительных температурах, что исключает периодическое образование в нем льда, нарушающего контакт между слоями;
3) ограждение более теплоустойчиво как к сквозному затуханию колебаний температуры наружного воздуха, так и к колебаниям теплопоступлений в помещение.
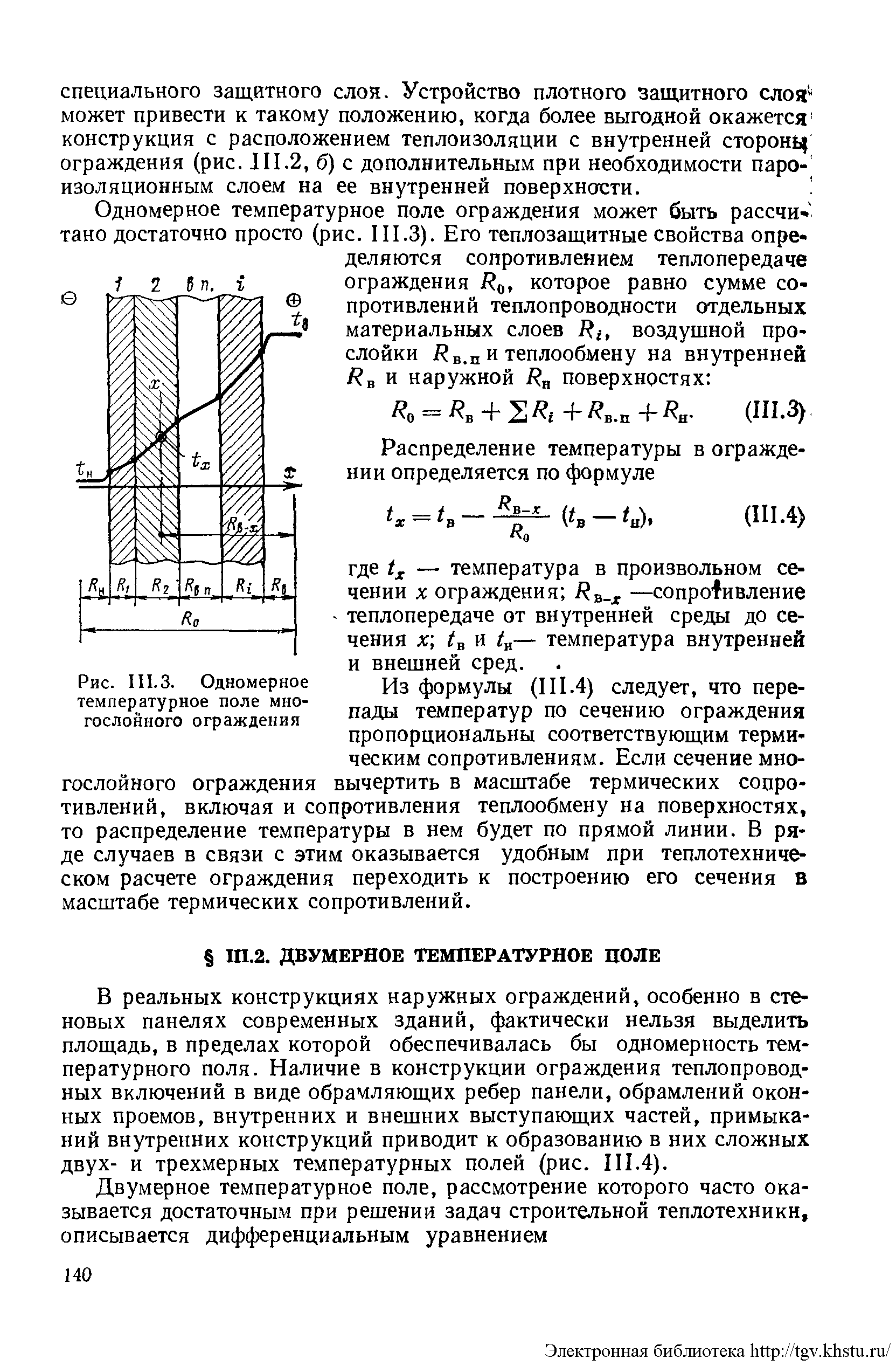
Одномерное температурное поле ограждения может быть рассчитано достаточно просто (рис.). Его теплозащитные свойства определяются сопротивлением теплопередаче ограждения Ro, которое равно сумме сопротивлений теплопроводности отдельных материальных слоев Ri, воздушной прослойки RВ.П и теплообмену на внутренней R и наружной Rн поверхностях:
Распределение температуры в ограждении определяется по формуле
где tx - температура в произвольном сечении х ограждения;
Rв-х -сопротивление теплопередаче от внутренней среды до сечения х;
tв и tн - температура внутренней и внешней сред.
Двумерное температурное поле
В реальных конструкциях наружных ограждений, особенно в стеновых панелях современных зданий, фактически нельзя выделить площадь, в пределах которой обеспечивалась бы одномерность температурного поля. Наличие в конструкции ограждения теплопроводных включений в виде обрамляющих ребер панели, обрамлений оконных проемов, внутренних и внешних выступающих частей, примыканий внутренних конструкций приводит к образованию в них сложных двух- и трехмерных температурных полей.
Двумерное температурное поле, рассмотрение которого часто оказывается достаточным при решении задач строительной теплотехники, описывается дифференциальным уравнением
где λ(х, у) - заданное значение теплопроводности отдельных частей двумерного сечения ограждения.
Решение этого уравнения значительно сложнее, чем уравнения для одномерного поля. Для большинства практических задач, когда наряду с двухмерностью поля приходится учитывать его неоднородность, аналитические методы не могут быть использованы. В этом случае применяют численные методы, которые достаточно точны и просты для расчета.
Рассмотрим основные методы решения двумерных температурных полей и примеры их использования для некоторых основных задач теплопередачи через ограждения.
Теплопередача через “тонкое” ребро.
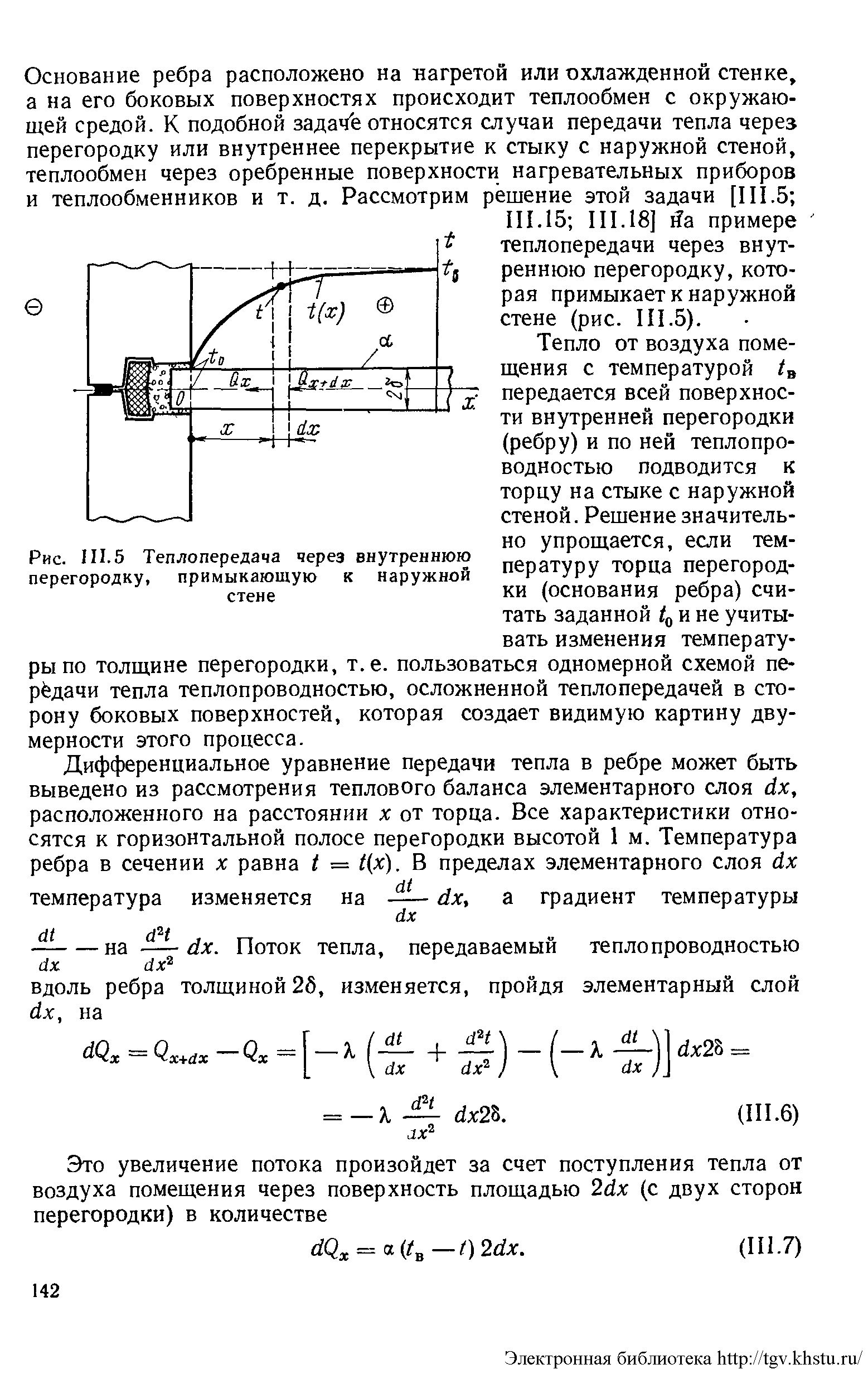
Дифференциальное
уравнение передачи тепла в ребре может
быть выведено из рассмотрения теплового
баланса элементарного слоя dx,
расположенного на расстоянии х от
торца. Все характеристики относятся к
горизонтальной полосе перегородки
высотой 1 м. Температура ребра в сечении
х равна t
= t(х).
В пределах элементарного слоя dx
температура изменяется на
,
а градиент температуры
- на
.
Поток тепла, передаваемый теплопроводностью
вдоль ребра толщиной 2δ изменяется,
пройдя элементарный слой dx
на
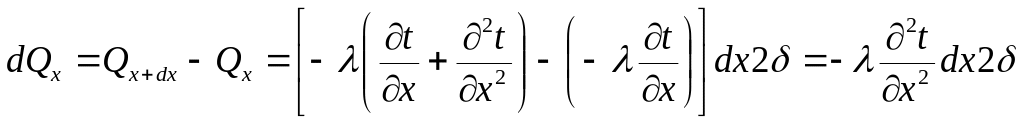
Это увеличение потока произойдет за счет поступления тепла от воздуха помещения через поверхность площадью 2dx (с двух сторон перегородки) в количестве
Коэффициент теплообмена а на поверхностях считается постоянным. Приравняв выражение () к (), получим уравнение теплового баланса элемента dx в виде
Коэффициент теплообмена а на поверхностях считается постоянным. Приравняв выражение () к (), получим уравнение теплового баланса элемента dx в виде
или
Для избыточной (относительно температуры окружающей среды tв) температуры ребра ϑ=t-tв уравнение будет иметь вид
где
Уравнение может быть записано в виде
где В – модификация критерия Био
Избыточная температура изменяется по длине перегородки по закону экспоненты.
Для расчета теплопотерь через стык перегородки со стеной нужно знать количество Qo тепла, подаваемого к торцу (х = 0) перегородки. Величина Q0
будет равна
или
rде
-
эквивалентный коэффициент теплообмена
на стыке перегородки со стеной.
Из сопоставления последних двух формул получим
Где
.
Величину
называют коэффициентом оребрения εр.
Он показывает увеличение теплообмена на поверхности за счет ребра при одинаковой разности температур.
Общее количество тепла, которое проходит через торец ребра. Qo
разделится между поверхностями пропорционально коэффициентам теплообмена. Например, количество тепла Q1, проходящее через боковую поверхность 1 ребра площадью Lх1 с α1 будет равно
При
разных температурах воздуха по сторонам
ребра
,
но одинаковых коэффициентах теплообмена:
α1=
α1=
α в расчетах нужно избыточные температуры
и другие определять относительно
средней -температуры:
Отношение теплоотдачи с двух поверхностей ребра будет равно отношению средних избыточных температур ребра:
Если и температуры воздуха и коэффициенты теплообмена по поверхностям ребра не равны, то необходимо пользоваться в расчетах средним значением α по формуле
а избыточные температуры определять относительно осредненной температуры
Часто на поверхности ребра расположены дополнительные материальные слои конструкции. Расчет такой конструкции значительно осложняется, так как ее надо рассматривать как двумерную. В инженерной практике можно пользоваться упрощенным решением, предполагая, что эти дополнительные слои являются только дополнительными термическими сопротивлениями теплообмену с поверхности тонкого ребра.
Теплопередача через “толстое” ребро.
В толстом ребре градиенты температуры в поперечном сечении становятся сопоставимыми с градиентами температуры вдоль ребра. При этом условии необходимо решать уравнение теплопроводности с учетом двухмерности температурного поля.
Простейшей является задача о теплопроводности толстого ребра при l=∞ и Бi →∞, когда на боковых поверхностях ребра неограниченной протяженности задана постоянная температура t(x=δ,y) = t(x=0,y)=tв, а на торце постоянная температура t(x,y=0)=t0. Точное решение задачи имеет вид
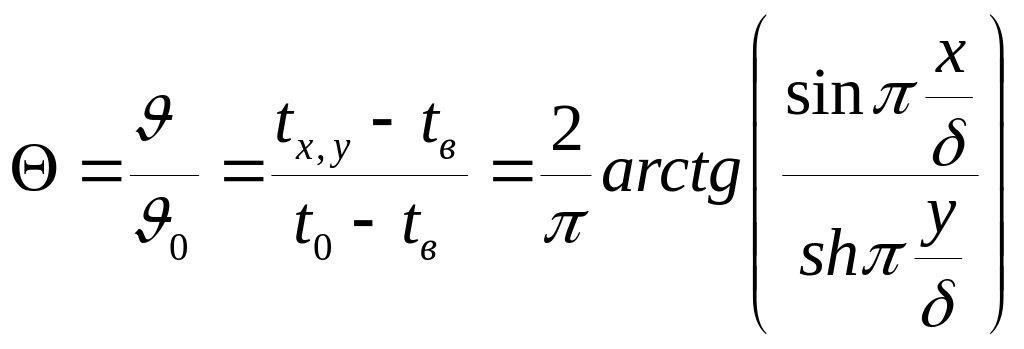
Относительная избыточная температура зависит только от относительных координат
Температурное поле толстого ребра с изотермическими поверхностями является крайним случаем, дающим наибольшую разницу с решением для тонкого ребра.
Распределение температуры по торцу толстого ребра в реальных условиях часто оказывается неравномерным. Если температуру торца ребра to принимать равной температуре в углу на стыке поверхности толстой перегородки с поверхностью стены, то расчетные формулы для тонкого ребра могут применяться для перегородок любой толщины. Погрешность расчетов не будет превышать 2% практически при всех значениях Вi.