8.2 Сетевые модели

Сетевая модель (сетевой график, сеть) представляет собой ориентированный граф, изображающий все необходимые для выполнения проекта операции в их взаимосвязи. Сетевые модели являются основным инструментом реализации проекта, именно с них началось развитие методологии управления проектом.

Сетевые модели позволяют:

- выполнять календарное планирование;

- оптимизировать использование ресурсов;

- сокращать или увеличивать продолжительность работ в зависимости от их стоимости;

- осуществлять оперативное руководство и контроль в ходе реализации проекта.

Основными элементами сетевой модели являются:

- работа;

- событие;

- путь.

Работа – это трудовой процесс, требующий затрат времени и (или) ресурсов. При построении сетевой модели работа отражается стрелкой, над которой указывается её продолжительность (обычно в днях). Работа идентифицируется (обозначается) номерами начального и конечного события, например 1-2, 2-5 и т.д. Для сложных сетевых моделей на графике возле стрелки, обозначающей работу (выше или ниже неё), могут указываться её наименование, стоимость, объем, ответственные исполнители, количество ресурсов.

Работой является и процесс ожидания, не требующий затрат труда, но требующий затрат времени. Ожидание изображается пунктирной стрелкой, над которой указывается его продолжительность.

К понятию «работа» относится и понятие «зависимость», или «фиктивная работа» - это связь между двумя или несколькими событиями, не требующая ни затрат времени, ни затрат ресурсов. Чаще всего зависимость возникает, когда начало одной работы осуществляется только после окончания другой. Фиктивная работа обозначается пунктирной стрелкой без указания времени.

Событие – это результат выполнения одной или нескольких работ, позволяющий начинать следующую работу. В сетевых моделях работа обозначается в виде круга. Событие, стоящее в начале сетевой модели, в которое не входит ни одна работа (стрелка), называется исходным событием. Событие, стоящее в конце сетевой модели, из которого не выходит ни одной работы (стрелки), называется завершающим.

Путь – это непрерывная последовательность работ от исходного до завершающего события сетевой модели. Длина пути определяется суммарной продолжительностью работ, лежащих на нем. Путь с наибольшей длиной называется критическим. Он определяет общую продолжительность проекта. Работы, входящие в критический путь, являются узкими местами и руководитель проекта должен сосредоточить свое внимание на своевременном выполнении этих работ, так как от этого зависит выполнение всех работ в установленный срок. Остальные работы имеют резерв времени, что позволяет маневрировать ресурсами или снижать стоимость работ за счет увеличения их продолжительности.

Виды сетевых моделей

В зависимости от формы представления и сделанных при построении графиков допущений выделяют разные виды сетевых моделей. Самой простой из них является структурная сетевая модель, или топология. Она представляет собой сетевую модель, которая не имеет каких-либо числовых показателей и обозначений.

По вариантности своей структуры сетевые модели делятся на две крупные группы: детерминированные и стохастические. Детерминированные сетевые модели – сетевые модели, события которых не имеют вероятностной характеристики, то есть они обязательно совершаются и совершаются в определенной последовательности, хотя продолжительность работ может иметь вероятностную оценку.

Стохастические сетевые модели – сетевые модели, в которых тот или иной комплекс последующих работ зависит от неизвестного ранее результата. Например, в зависимости от результатов обследования грунта может предусматриваться несколько вариантов устройства фундамента сооружения и укрепления грунта. Продолжительность отдельных работ в стохастических сетевых моделях может быть либо постоянной (детерминированной), либо случайной величиной.

В том случае, когда в детерминированной или стохастической модели не известна точная продолжительность работ, но её можно прогнозировать с определенной степенью вероятности, строится сетевая модель с вероятностной оценкой продолжительности работ соответствующего типа (стохастическая или детерминированная).

В зависимости от количества поставленных целей, которые становятся завершающими событиями, различают одноцелевые сетевые модели и многоцелевые сетевые модели. Последний вид моделей используется в управлении проектами при решении задач управления несколькими проектами одновременно, либо управления сложными многоцелевыми проектами и программами. В многоцелевых моделях допускается существование нескольких завершающих событий. Методика их расчета аналогична расчету одноцелевого графика, с той особенностью, что в многоцелевой модели будет столько критических путей, сколько завершающих событий.

Так как наибольшее распространение имеют одноцелевые сетевые модели, рассмотрим правила их построения, большая часть которых подходит и для многоцелевых сетевых моделей.

Правила построения одноцелевых сетевых моделей [4]:

1. Правило последовательности изображения работ: сетевые модели следует строить от начала к окончанию, то есть слева направо.

2. Правило изображения стрелок: в сетевом графике стрелки, обозначающие работы, ожидания или зависимости, могут иметь различный наклон и длину, но должны идти слева направо и всегда направляться от предшествующего события к последующему. Следует избегать пересечения стрелок, чем меньше пересечений, тем нагляднее график.

3. Правило обозначения работ: в сетевом графике между обозначениями двух смежных событий может проходить только одна стрелка.

4. Правило расчленения и запараллеливания работ: при построении сетевого графика можно начинать последующую работу, не ожидая полного завершения предшествующей. В этом случае нужно «расчленить» предшествующую работу на две, введя дополнительное событие в том месте предшествующей работы, где может начаться новая.

5. Правило запрещения замкнутых контуров (циклов, петель): в сетевой модели недопустимо строить замкнутые контуры – пути, соединяющие некоторые события с ними же самими. Недопустимо, чтобы один и тот же путь возвращался в событие, из которого он вышел.

6. Правило запрещения тупиков: в сетевом графике не должно быть тупиков, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события. Следует отметить, что это правило имеет исключение для многоцелевых графиков, где завершающих событий несколько.

7. Правило запрещения хвостовых событий: в сетевом графике не должно быть хвостовых событий, т.е. событий, в которые не входит ни одна работа, за исключением начального события.

8. Правило изображения дифференцированно-зависимых работ: если одна группа работ зависит от другой группы, но при этом одна или несколько работ имеют дополнительные зависимости или ограничения, при построении сетевого графика вводят дополнительные события.

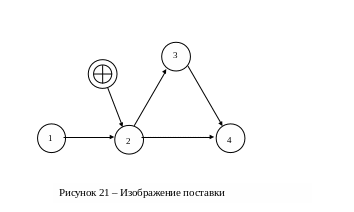
9. Правило изображения поставки. Поставкой в сетевом графике является любой результат, который предоставляется «со стороны», то есть не является непосредственно результатом работы непосредственного участника проекта. В сетевом графике поставки изображаются двойным кругом, либо другим знаком, отличающимся от знака обычного события данного графика. Рядом с кругом дается ссылка на документ (контракт или спецификацию), раскрывающий содержание и условия поставки. Пример изображения поставки приведен на рисунке 21.

10. Правило учета непосредственных примыканий (зависимостей): в сетевом графике необходимо учитывать только непосредственное примыкание (зависимость) между работами.

11. Технологическое правило построения сетевых графиков: для построения сетевого графика необходимо в технологической последовательности установить:

- какие работы должны быть завершены до начала данной работы;

- какие работы должны быть начаты после завершения данной работы;

- какие работы необходимо выполнять одновременно с выполнением данной работы.

12. Правила кодирования событий сетевого графика:

- все события графика должны иметь свои собственные номера;

- кодировать события необходимо числами натурального ряда без пропусков;

- номер последующему событию следует присваивать после присвоения номеров предшествующим событиям;

- стрелка (работа) должна быть всегда направлена из события с меньшим номером в событие с большим номером.