24. Математические основы измерения и анализа случайных динамических процессов мехатронных систем

Процесс, для которого характерно изменение физической вели­чины во времени случайным образом, называют случайным. Он описывается случайной функцией времени. Когда аргумент случайной функции является пространственной переменной, то такая функция описывает случайное поле. Случайную функцию можно рассматривать как бесконечную совокупность, множество, ансамбль функций, каждая из которых представляет собой одну из возможных реализаций случай­ной функции.

Случайные функции обозначают большими буквами латинского ал­фавита: X(t), Y(t, Z(t) , а реализации - малыми буквами: x(t), у(t), z(t) . Таким образом, случайный процесс, описывае­мый случайной функцией X (t) - это ансамбль, множество реали­заций x₁(t), x₂ (t), …. x_k(t),…, x_(t).

В соответствии с тем, возможен или нет сдвиг начала отсчета вероятностных характеристик во времени, случайные процессы делят на стационарные и нестационарные.

Стационарным называется такой случайный процесс, у которого определенная группа вероятностных характеристик инвариантна во времени, т.е. не изменяется при сдвиге времени - замене аргумен­та t значением t + , где  - произвольный интервал вре­мени. Различают стационарные процессы в узком смысле и широком смысле.

Случайный процесс называют стационарным в узком смысле, ес­ли n -мерные функции распределения вероятностей ( п - конечная величина произвольного порядка) не изменяются во времени, т.е. выражения для плотности распределения вероятностей любого поряд­ка не зависят от выбора момента начала отсчета времени. Математи­чески это означает, что для любых п и t справедливо равенст­во

(24.1)

Для стационарных в широком смысле случайных процессов харак­терно, что математическое ожидание и дисперсия не зависят от вре­мени, а корреляционная функция зависит лишь от разности времен.

Случайные процессы, стационарные в узком смысле, стационар­ны и в широком смысле, но не наоборот.

Нестационарные случайные процессы - это процессы, вероятност­ные характеристики которых являются функциями времени и зависят от начала отсчета.

Применительно ко многим случайным процессам допустима эргодическая гипотеза. О таких процессах говорят, что они эргодичны по отношению к определенной вероятностной характеристике. Отли­чительная особенность эргодического процесса заключается в том, что его вероятностные характеристики могут быть получены с вероятностью, сколь угодно близкой к единице, в результате некоторой операции усреднения по времени одной реализации достаточно боль­шой (теоретически бесконечной) длительности.

Эргодическое свойство очень важно для исследования случай­ных процессов, так как позволяет усреднение по ансамблю заменять усреднением по времени.

Случайные процессы разделяют на непрерывные и дискретные в зависимости от того, непрерывен ли аргумент t по всей оси (на рассматриваемом отрезке) или принимает дискретные значения. Непрерывными (континуум значений) или квантованными могут быть и ординаты случайной функции.

Признаком классификации служит также характер распределения вероятностей случайного процесса, вид кривой плотности распределения. Различают гауссовский, релеевский процессы, процесс с равномерным распределением и т.д.

Особое место занимает гауссовский процесс, охватывающий ши­рокий класс явлений и часто наблюдаемый в технике.

Процесс называют гауссовским, если все его n -мерные плот­ности распределения вероятностей подчиняются нормальному закону. Подобный закон распределения наблюдается во всех случаях, когда исследуемый процесс можно представить в виде суммы большого чис­ла независимых или слабо зависимых слагаемых при условии отсутст­вия среди них таких, значения которых значительно превышают зна­чения большинства остальных.

Основные свойства гауосовского процесса:

1. Случайный процесс исчерпывающим образом определяется за­коном изменения во времени математического ожидания и корреля­ционной функции (этим объясняется то, что корреляционная теория дает полное описание гауссовских процессов). Процессы могут отли­чаться друг от друга значением математического ожидания и видом корреляционной функции.

2. Стационарный в широком смысле гауссовский процесс ста­ционарен и в узком смысле.

3. Сумма двух гауссовских процессов также представляет гауссовский процесс.

4. Некоррелированные гауссовские процессы - процессы незави­симые.

5. Линейные преобразования гауссовского процесса не меняют его характера.

6. Распределение вероятностной производной гауссовского стационарного процесса, описываемого непрерывной и дифференци­руемой случайной функцией, также нормально.

7. Нелинейное преобразование нарушает свойство нормальнос­ти процесса.

Зависимость поведения случайной функции от ее значений в предшествующие моменты времени позволяет классифицировать случай­ные процессы по следующим видам:

а) белый шум - процесс, описываемый случайной функцией, последовательные значения которой статистически независимы от предыдущих значений, как бы ни были малы разделяющие их проме­жутки времени. Такой процесс полностью определяется одномерной плотностью распределения вероятностей;

б) марковский процесс - процесс, у которого зависимость те­кущего значения от предистории не распространяется далее непосредственно предшествующего момента. Вероятностные свойства случайной функции, описывающей марковский процесс, полностью определяются двумерной плотностью распределения вероятностей; в) немарковские процессы.

Основой деления случайных процессов на узкополосные и широко­полосные является относительная ширина полосы частот (по отноше­нию к средней частоте), в которой главным образам сосредоточен спектр мощности процесса.

Различают случайные, смешанные и квазидетерминированные про­цессы.

Случайным называют процесс, в котором отсутствуют детерминированные составляющие. От такого процесса отличают смешанный про­цесс, представляющий собой совокупность случайного процесса и де­терминированных составляющих - периодических или апериодических неслучайных функций времени. Типичным примером - служит аддитивная смесь шума и полезного сигнала.

Квазидетерминированные случайные процессы характеризуются тем, что их реализации описываются функциями времени определенно­ о вида, содержащими один или несколько случайных параметров, не зависящих от времени. В качестве примера можно привести процесс вида: x(t) =A cos (₀t-), где А и ₀ - фиксированы, a  - случайная фаза.

Функция распределения вероят­ностей случайного процесса, описывае­мого случайной функцией X (t) в фиксированный момент времени t = t₁ , определяет вероятность того, что в указанный момент любое значение случайного процесса меньше некоторого значения (уровня) x, которое можно варьировать.

Функция распределения задается соотношением

(24.2)

Для эргодического стационарного случайного процесса функция распределения может быть определена по одной реализации. Она ха­рактеризуется относительным временем пребывания значений реали­зации длительности Т  ниже заданного уровня X.

Свойства функции распределения:

(24.3)

F(x)- неубывающая функция аргумента х; график функции по­всюду непрерывен слева.

Функция распределения равномерной случайной последователь­ности определяется зависимостью

(24.4)

Если случайная последовательность получена выборками из не­прерывного случайного процесса его значений в моменты i Т₀, то функция распределения случайной последовательности не отлича­ется от функции распределения случайного процесса при условии замены t на i Т₀.

Плотность распределения вероят­ностей случайного процесса представ­ляет собой производную от функции распределения

(24.5)

При этом c точностью до бесконечно малой величины высшего порядка справедливо равенство

(24.6)

Если исследуется стационарный эргодический процесс, то

Основные свойства плотности вероятностей:

. (24.7)

Для равномерной случайной последовательности плотность ве­роятностей определяется выражениями:

(24.8)

Математическое ожидание случай­ной функции X(t) -такая функция т_х (t), значение которой при каждом данном значении аргумента t равно математическому ожиданию значения случайной функции X (t) при данном t:

(24.9)

Математическое ожидание случайной функции представляет собой некоторую среднюю функцию, около которой группируются и от­носительно которой колеблются все возможные реализации случайной функции.

Для действительной случайной функции X (t) математическое ожидание может быть вычислено по формуле

(24.10)

где р (X, t) - плотность вероятности.

У стационарных случайных процессов математическое ожидание не зависит от времени и представляет собой постоянное число Если процесс не только стационарен, но и обладает эргодическим свойством (по отношению к математическому ожиданию), то у такого процесса среднее по ансамблю равно о вероятностью единица сред­нему по времени, определяемому по одной реализации:

(24.11)

причем временное среднее находится из формулы

в предположении, что предел существует.

Если исследуемый случайный процесс представляет собой электрическое напряжение или ток, то среднее значение - это постоян­ная составляющая напряжения или тока.

Для равномерной случайной последовательности Х(i Т₀) сред­нее по ансамблю реализаций

(24.12)

При условии, что случайной последовательности присуще эргодическое свойство, ее математическое ожидание может быть найдено как среднее арифметическое по времени одной реализации

, (24.13)

если этот предел существует.

Дисперсия случайной функции (t) есть такая функция, значение которой при каждом данном значении аргумента t равно дисперсии случайной функции при этом значении аргумента

(24.14)

Дисперсия характеризует рассеяние возможных реализаций слу­чайной функции относительно математического ожидания. Она пред­ставляет собой центральную моментную функцию второго порядка

(24.15)

Для стационарного эргодического случайного процесса выражение дисперсии принимает вид:

(24.16)

и характеризуется постоянным числом.

Если исследуемым случайным процессом является напряжение или ток (сопротивление нагрузки 1 Ом), то член соответствует полной средней мощности процесса, член - мощности пос­тоянной составляющей, а дисперсия D_x - мощности переменной составляющей.

При равномерной случайной последовательности

(24.17)

Когда процесс стационарен и эргодичен (по отношению к дисперсии), то

(24.18)

Дисперсия характеризует рассеяние в квадратичной мере. Поэ­тому на практике часто используют в качестве подобной характерис­тики среднее квадратическое отклонение, представляющее собой ко­рень квадратный из дисперсии, взятый со знаком плюс: Корреляционная функция случайного процесса характеризует тесноту стохастической связи между значениями случайного процесса в различные моменты времени. В общем случае она является функцией двух аргументов t₁ и t₂ и представляет собой математическое ожидание произве­дений центрированных значений случайной функции для этих двух аргументов

(24.19)

Значение корреляционной функции при равных значениях аргументов t₁ = t₂ = t дает дисперсию случайного процесса

Корреляционная функция нестационарного случайного процесса графически изображается пространственной фигурой.

Если случайный процесс стационарен хотя бы в широком смысле, то корреляционная функция является функцией лишь разности = t₁ - t₂ аргументов, а не их абсолютных значений и принимает одно и то же значение при всех аргументах t₁ и t₂, отличаю­щихся один от другого на одинаковую величину :

(24.20)

Когда случайная последовательность стационарна и обладает эргодическим свойством, корреляционная функция описывается выра­жением

, (24.21)

где

Для стационарных эргодических процессов можно отметить сле­дующие свойства:

1. При

Rx()0

2. Корреляционная функция любой периодической квазидетерминированной функции аргумента t обладает такой же периодичнос­тью при аргументе .

Для характеристики взаимосвязи между значениями двух случайных процессов X(t) и Y(t) служит взаимная корреляционная функ­ция, определяемая выражением

(24.22)

Для характеристики случайного процесса в целом пользуются понятиями спектральной плотности или спектра.

Спектральная плотность S_x (f) стационарного эргодического случайного процесса X (t) выражает среднюю мощность процесса, приходящуюся на единицу полосы частот.

Спектр S_x (f) стационарного случайного процесса связан о корреляционной функцией их R_x() этого процесса парой преобразова­нии Фурье (теорема Винера-Хинчина):

(24.23)

Основные свойства спектральной плотности стационарного слу­чайного процесса:

1. Спектральная плотность неотрицательна, т.е. при любом значении f

2. При ограниченной дисперсии случайного процесса

3. Спектральная плотность является вещественной функцией f.

4. Спектральная плотность - четная функция, т.е.

5. Интеграл от спектральной плотности равен дисперсии ста­ционарного случайного процесса

6. Изменение масштаба т аргумента  корреляционной функ­ции вызывает обратное изменение масштаба частоты f и величины спектральной плотности S_x(f) , т.е. если R₂()= R₁ (m),тo соответственно

7. Спектральная плотность процесса на выходе линейной систе­мы с постоянными параметрами S_y (f) связана со спектральной плотностью стационарного случайного процесса на входе системы S_x (f) выражением

,

где K(f) - амплитудно-частотная характеристика системы.

С учетом свойств 3 и 4 можно выразить спектральную плотность мощности через корреляционную функцию формулой

Взаимной спектральной плотностью стационарно связанных слу­чайных процессов X(t) и Y(t) называют преобразование Фурье от взаимной корреляционной функции этих процессов

Основные свойства взаимной спектральной плотности:

1. Взаимная спектральная плотность S_xy(f) в общем случае величина комплексная.

Ее вещественная часть Re S_xy (f) является четной функцией, а мнимая часть Im Sxy(f) - функцией нечетной:

(24.24)

2. Интеграл от взаимной спектральной плотности S_xy(f) в бесконечных пределах аргумента f дает взаимную дисперсию случайных процессов:

3. Изменение масштаба аргумента  взаимной корреляционной функции R_XY () вызывает такие же изменения взаимной спектральной плотности S_xy (f) , что и изменение масштаба  функции корреляции Rxy() у спектральной плотности S_x (f), т.е. функция R_xy (m) соответствует функции

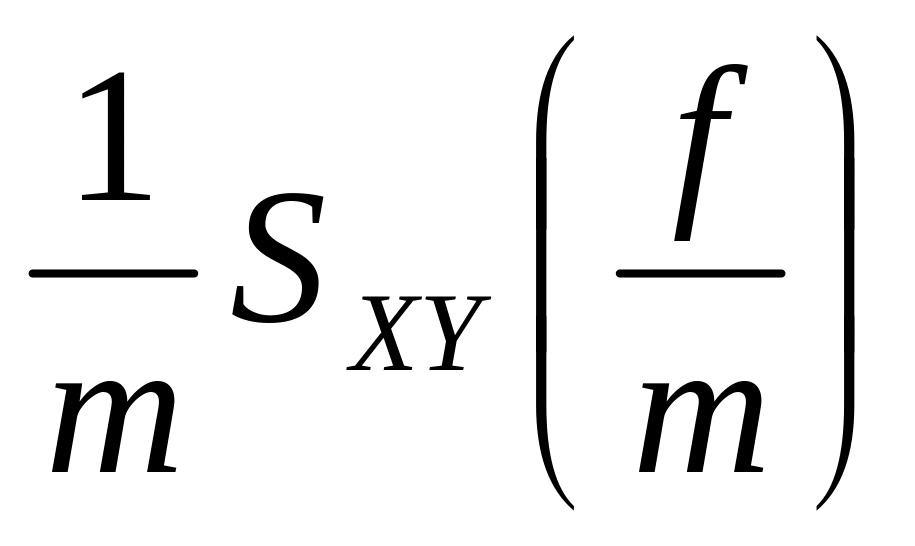
4. Взаимные спектральные плотности S_xy (f) и S_yx (f) являются комплексно сопряженными величинами и связаны соотноше­ниями

Рассмотренными характеристиками не исчерпывается описание случайных динамических процессов, но они являются основными для принятого в пособии математического описания рассмотренных моде­лей.