17. Расчет и выбор параметров сглаживающего фильтра

Для снижения пульсации выпрямленного напряже­ния на выходе преобразователя-выпрямителя устанав­ливается сглаживающий фильтр. Эффективность сгла­живающего фильтра оценивают по его способности уменьшать амплитуду пульсации, т.е. по значению ко­эффициента сглаживания q_c.

17.1. Расчет коэффициента сглаживания

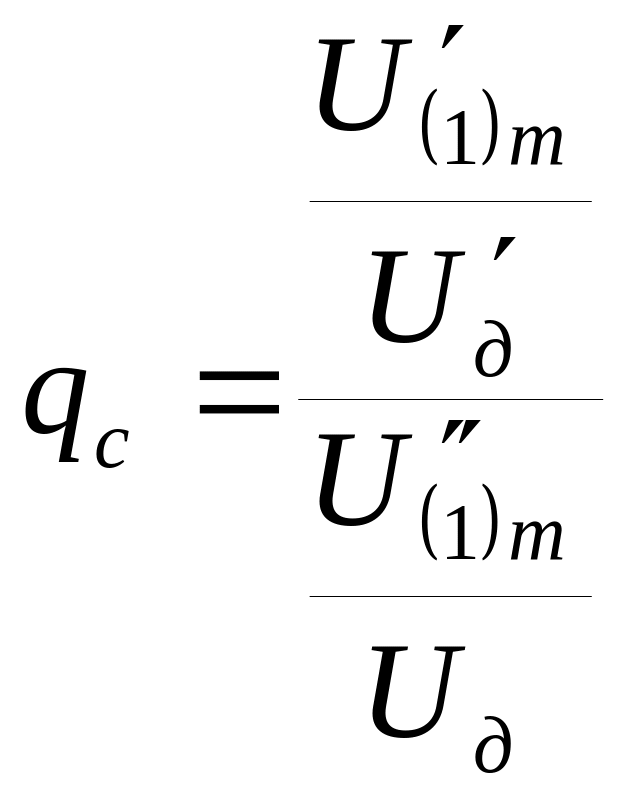(17.1)

где U'_(1)m , U'_д— амплитуда основной гармоники пульсаций и постоянная составляющая напряжения на входе фильтра U'_(1)m= 183,6⁶ В, U'_д=274 В; , U''_(1)m, U_д - амплитуда основной гармоники пульсаций и постоянная сглаживающая напряжения на выходе фильтра, U''_(1)m = 1В, U_д = 274 .В.

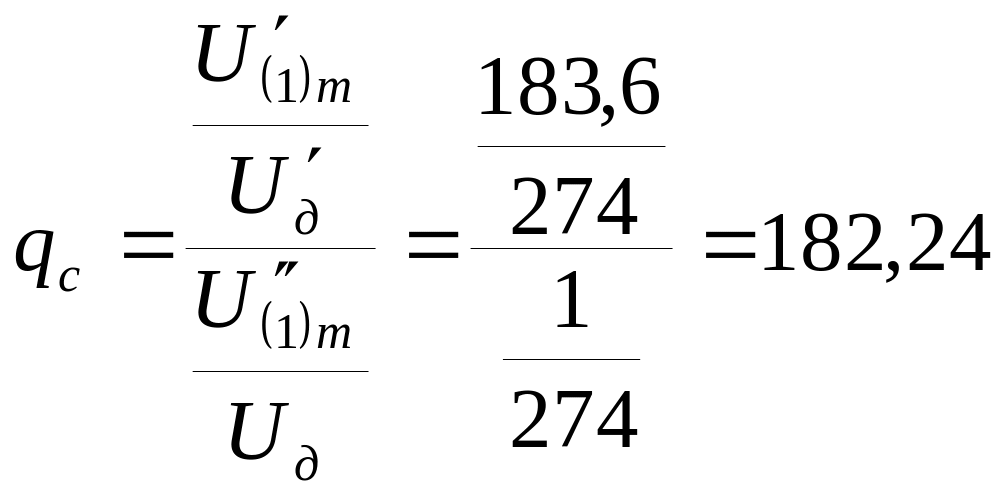
17.2. Выбор схемы фильтра

В соответствии с рекомендациями выбираем Г-образный LC-фильтр. Определяем, произведение L_д • С

(17.2)

где m_n — частота пульсаций выпрямленного напряже­ния, m_n = 100 Гц;

_c=314,16рад/с

17.3. Определение минимального значения индук­тивности дросселя

Гн

По рассчитанному значению L_д..мин выбираем стан­дартный дроссель фильтра ДПМ 200-1000 со следующи­ми параметрами:

• индуктивность дросселя L_д, 10^-6 Гн.... 1000

• номинальный постоянный ток, А ....................200

17.4. Расчет емкости конденсатора фильтра

(17.3)

17.5. Рабочее напряжение конденсатора

Рабочее напряжение конденсатора при проектирова­нии выбирается больше значения выпрямленного на­пряжения из выражения

В (17.4)

По рассчитанному значению емкости С и рабочему напряжению выбираем конденсатор К50-78-450В — 220мкФ ± 20%.

18. Кинематическая погрешность цилиндрической зубчатой передачи

Точность работы мехатронного модуля оценивают его погреш­ностью, т.е. разностью между действительным и расчетным поло­жениями выходного звена. Основными причинами возникновение погрешности мехатронного модуля являются погрешности систем управления и двигателя, кинематические погрешности, мертвые ход и упругие деформации элементов его преобразователей движе­ния.[10]

Из-за наличия погрешностей изготовления зубчатых колес и сбор­ки передачи угол ₂ поворота ведомого колеса реальной зубчаток передачи отличается от угла поворота ведомого колеса идеального механизма при одном и том же значении угла , поворота ведуще­го зубчатого колеса (рис. 18.1):

, (18.1)

где u₁₂ - передаточное отношение от первого зубчатого колеса ко второму; - боковой зазор между зубьями ведущего и ведомого зубчатых колес; R₂ - радиус ведомого зубчатаго колеса; ₂ - по­грешность положения ведомого колеса.

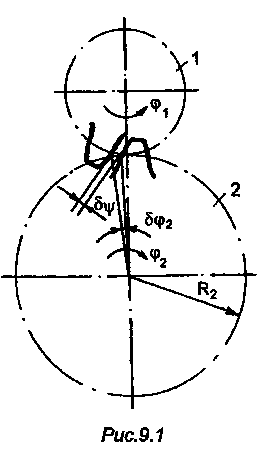
Рис. 18.1. Погрешности изготовления и сборки зубчаты колес

Алгебраическую разность между погрешностями положения ведомого колеса, вызванную погрешностями из­готовления и сборки передачи, назы­вают кинематической погрешностью передачи.

Кинематическую погрешность ци­линдрической зубчатой передачи определяют ме­тодом максимума-минимума и вероят­ностным методом.

При расчете по методу максимума-минимума минимальное значение ки­нематической погрешности F{_0min зуб­чатой цилиндрической передачи по ду­ге делительной окружности ведомого

(18.2)

Максимальное значение кинематической погрешности, мкм:

, (18.3)

где А - коэффициент, учитывающий степень точности передачи. . Для зубчатой передачи 7-й и 8-й степеней точности А=0,71, для остальных степеней точности А=0,62; К_s и К- коэффициенты фазовой компенсации, принимаемые в зависимости от передаточного отношения и по табл. 18.1; F`_i - допуск, мкм, на кинематическую по­грешность колеса:

F_р - допуск, мкм, на накопленную погрешность шага зубчатого колеса, f_f - допуск на погрешность профиля зуба; Е_M — суммарная приведенная погрешность монтажа, мкм:

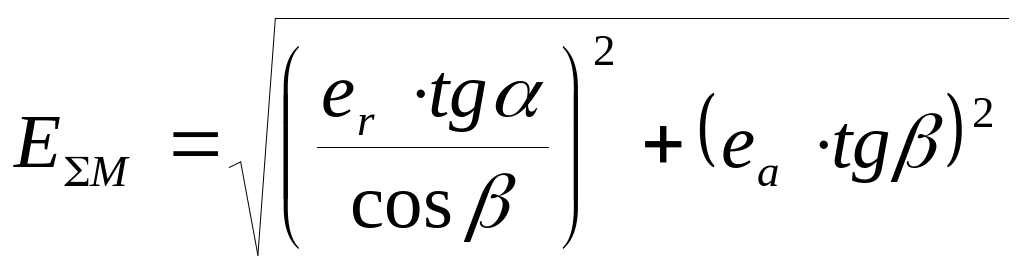
где = 20° — угол зацепления, град;  - угол наклона линии зуба, град; e_r = F_r - монтажное радиальное биение зубчатого колеса, мкм:

е_i - допуски на погрешности, создающие первичные радиальные биения колеса, мкм; е_а - монтажное осевое биение зубчатого коле­са, мкм:

e_j — допуски на погрешности, создающие первичные осевые бие­ния колеса, мкм.

В предварительных расчетах можно принимать е_а=5...15 мкм.

Таблица 18.1

Значения коэффициентов фазовой компенсации для зубчатой передачи

и	К	Ks
1,0...1,5	0,98	0,30
1.5...2.0	0,85	0,76
2,0...2,5	0,83	0,75
2.5...3.0	0,93	0,74
3,0...3,5	0,97	0,75
3,5...4,0	0,96	0,80
4,0..4…5	0,96	0,90
4.5...5.0	0,96	0,87
5Д..5.5	0,98	0,85
5.5...6.0	0,96	0,88
6Д.Д5	0,97	0,94
Св. 6,5	0,98	0,99
Примечание. Для передаточных отношений, не выражаемых целым в случае числом, работы передачи в пределах больше одного оборота колеса K=KS=0,98

При вероятностном методе расчета максимальное значение ки­нематической погрешности цилиндрической зубчатой переда­чи, мкм:

, (18.4)

где К_р— вероятностный коэффициент фазовой компенсации, при­нимаемый в зависимости от передаточного отношения и и процен­та риска Р по табл. 18.2.

Таблица 18.2

Значения вероятностного коэффициента фазовой компенсации К_р для зубчатых передач

Р,%	Передаточное отношение u
	1,0... 1 5	1,5... 2,0	2,0... 2,5	2,5... 3,0	3,0... 3,5	3,5... 4,0	4,0... 4,5	4,5... 5,0	5,0... 5,5	5,5... 6,0	6,0... 6,5	Св. 6,5
32	0, 58	0,68	0,60	0,74	0,71	0,71	0,68	0,71	0,78	0,70	0,78	0,80
10	0, 92	0,78	0,73	0,88	0,82	0,82	0,80	0,82	0,90	0,88	0,91	0,94
4,5	0 ,95	0,83	0,81	0 91	0,92	0,91	0,88	0,92	0,94	0,94	0,94	0,96
1,0	0,96	0,84	0,82	0,92	0,95	0,95	0,94	0,95	0,97	0,95	0,96	0,96

Пересчет значений кинематической погрешности , выра­женной в мкм, в угловые единицы-минуты, (...'), получим из про­порции

где d₂ - диаметр делительной окружности ведомого зубчатого коле­са, мм.

Откуда кинематическая погрешность 5ср цилиндрической зуб­чатой передачи в угловых единицах, (...'):

(18.5)

Кинематическая погрешность цилиндрической зубчатой пере­дачи в радианах, (рад):

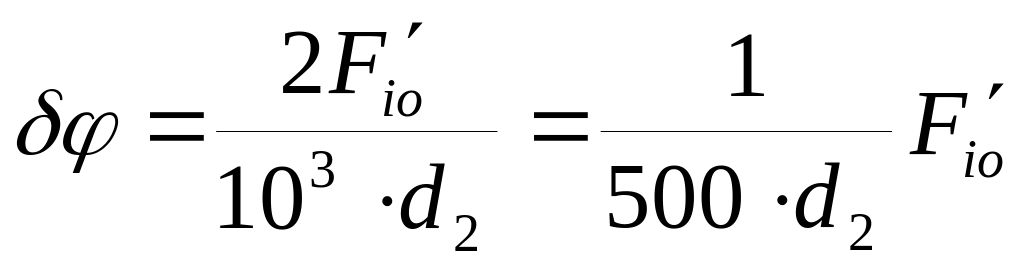(18.6)