1.4 Математические основы информатики

1.4.1. Алгебра высказываний (булева алгебра)

Основное понятие булевой алгебры – выказывание. Под простым высказыванием понимается повествовательное предложение, о котором можно сказать, истинно оно или ложно, поэтому высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (0) или ИСТИНА (1). Например, содержание высказывания А: «дважды два равно четырем» истинно А = 1, а высказывание В: «три больше пяти» всегда есть ЛОЖЬ. В дальнейшем нас не будет интересовать содержательная часть высказываний, а только их истинность. Два высказывания А и В называются равносильными, если они имеют одинаковые значения истинности, записывается А = В.

Сложное высказывание можно построить из простых с помощью логических операций: отрицания, конъюнкции, дизъюнкции, импликации и логических выражений, представляющих собой комбинации логических операций. Рассмотрим их подробней.

О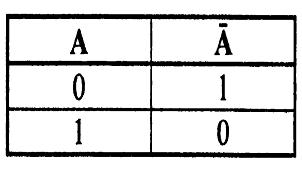 перацией отрицания А (А, не А) называют высказывание А, которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «завтра будет снег», то А - «завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Отрицание – унарная (т.е. для одного операнда) логическая операция.

К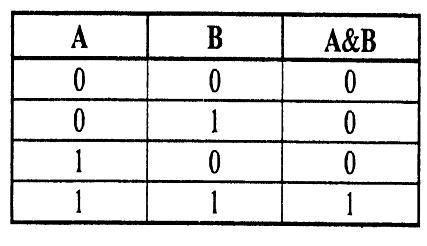 онъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается С = А  В или С = А & В (С равно А и В). Например, пусть высказывание А «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, если ширина шкафа меньше ширины двери И высота шкафа меньше высоты двери».

Д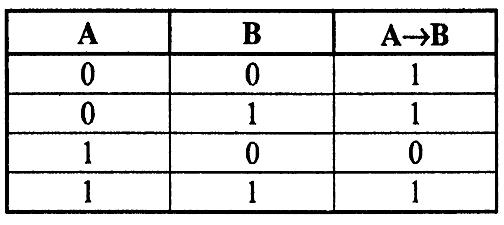 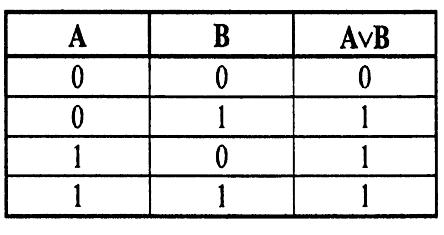изъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается С = A  В (С равно А ИЛИ В). Пример: высказывание А «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллейбусе», событие С «студент добрался домой на автобусе ИЛИ троллейбусе».

Импликацией двух высказываний А (А - посылка) и В (В - заключение) является новое высказывание С, которое ложно только тогда, когда посылка истинна, а заключение ложно, записывается С = А  В (из А следует В). Пример: если произошло событие А, то произойдет событие В, «если идет дождь, то на небе тучи». Операция не симметрична, т.е. из В  А не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно.

Эквиваленцией двух высказываний А и В является новое выс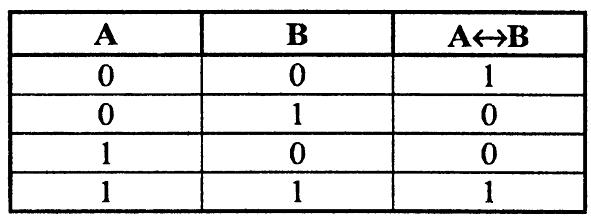 казывание С, которое истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается С = А  В (С = А  В).

С помощью логических операций из простых высказываний (логических переменных и констант) можно построить логические

выражения, которые также называются булевскими функциями. Например, С = ((  В)  В)  А. Чтобы избежать большого количества скобок в булевских функциях, принято соглашение о старшинстве операций. Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.

Операции не являются независимыми; одни из них могут быть выражены через другие. Можно доказать с помощью таблиц истинности следующие равносильности:

= А	закон двойного отрицания
А & В = В & А	коммутативный закон для конъюнкции
A  B = B  A	коммутативный закон для дизъюнкции
(А & В) & С = А & (В & С)	ассоциативный закон для конъюнкции
(A  B)  C = A  (B  C)	ассоциативный закон для дизъюнкции
А & (В  С) = (А & В)  (А & С)	дистрибутивные законы
A  (В & С) = (A  В) & (A  С)
	законы де Моргана
А & А = А	закон идемпотенции для конъюнкции
A  A = А	закон идемпотенции для дизъюнкции
А & 1 = А	закон единицы для конъюнкции
А & 0 = 0	закон нуля для конъюнкции
A  1 = 1	закон единицы для дизъюнкции
A  0 = А	закон нуля для дизъюнкции
A  = 1	закон исключения третьего
А & = 0	закон противоречия
А  В =  В
А  В = (А  В) & (В  А) = (  В) & (A  ) = (A & B)  ( & )
A  (А & В) = А	законы поглощения
А & (A  В) = А
А & (  B) = A & B
A  ( & В) = A  В

Одну и ту же зависимость между логическими переменными можно выразить различными формулами. Поэтому важно иметь возможность приводить формулы с помощью эквивалентных преобразований к некоторому стандартному виду. Существует несколько стандартных форм, к которым приводятся логические выражения с помощью эквивалентных преобразований.

Первая из них – дизъюнктивная нормальная форма (ДНФ), имеет вид A_l  A₂  ...  A_n, где каждое из составляющих высказываний есть конъюнкция простых высказываний и их отрицаний, например:

В = ( & А₂ & A₃)  (А₄ & А₅).

Вторая – конъюнктивная нормальная форма (КНФ), имеет вид А₁  А₂  ...  A_n, где каждое из составляющих есть дизъюнкция простых высказываний и их отрицаний, например:

В = .