Задание 4 Условие:

Для перевода производства на новую, более прогрессивную технологию необходимо осуществить комплекс мероприятий. Известны продолжительности выполнения каждой работы и количество специалистов, необхо­димых для выполнения этих работ.

Требуется:

1 Построить временной сетевой график выполнения комплекса работ.

2 Определить критический путь.

3 Найти минимальное время выполнения всего комплекса работ.

4 Найти минимальное количество человек R, которое потребуется для выполнения этого комплекса работ.

Информация о комплексе работ для каждого варианта приведена ниже.

Работа	Опирается на работы	Характеристики работы
		Время выполнения, дни	Затраты трудовых ресурсов, чел.
		5	3
		4	2
		6	2
		4	5
		6	4
		4	6
		5	3
		7	2
		6	5

Решение.

Исходное событие означает момент начала выполнения проекта. Работам , , не предшествуют никакие работы, следовательно, на графике они изображены дугами, выходящими из исходного события . Событие означает момент окончания работы . Работе предшествуют работы . На графике эта зависимость отражена с помощью введения фиктивной работы ( ). Моментом свершения события будет момент, к которому будут выполнены работы и и может начинаться работа .Работе предшествуют работы . Работе предшествуют работа . Аналогично, с учетом взаимосвязей изображаются на графике все оставшиеся работы. Завершающее событие А означает момент выполнения всего проекта (рисунок 3)

Критический путь – это путь из точки к точке А, не содержащий фиктивных работ. Он состоит из критических работ a_1, a_4, a_6, a_7, a_9, a_8, a₃. Тогда критическое время выполнения проекта будет

.

Н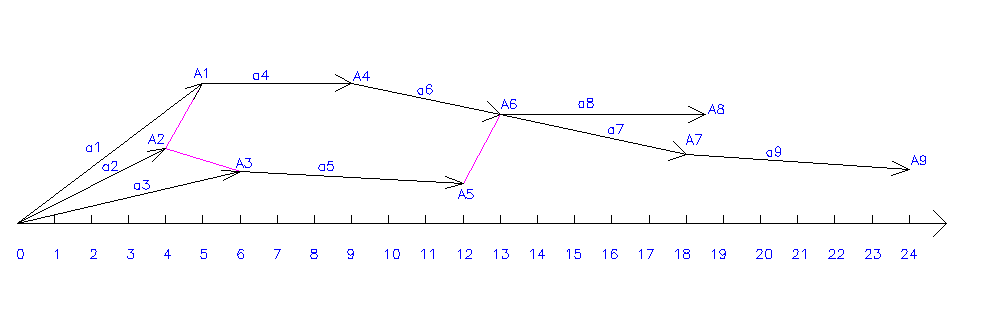 а рисунке 3 построен временной сетевой график.

Рисунок 3

Для определения числа исполнителей, необходимого для выполнения всего комплекса работ, построим шкалу потребления ресурса. Обозначим на временном сетевом графике число исполнителей для каждой работы (в скобках около наименования работы, т.е. ( )). На ось времени Оt сетевого графика проектируют пунктирными линиями начальные и конечные точки всех работ и получают промежутки постоянства интенсивности потребления ресурса. Суммарную потребность в ресурсе в данном временном промежутке определяют, суммируя интенсивности всех работ, расположенных над этим промежутком (см. рисунок 4).

Максимальное число исполнителей (10 человек) требуется на промежутке времени [9,12]. Следовательно, R=10.Таким образом, для выполнения данного проекта потребуется минимум 10 человек.

Рисунок 4