Задача к-7 Определение скоростей и ускорений точек многозвенного механизма

В данной задаче изучается плоскопараллельное движение твердых тел. Плоскопараллельное движение можно считать состоящей из поступательного движения вместе с полюсом и из вращательного движения вокруг полюса. За полюс выбирается любая точка плоской фигуры. Угловая скорость ω, угловое ускорение ε плоской фигуры не зависят от выбора полюса.

Скорости точек плоской фигуры находятся по теореме о скоростях: скорость любой точки плоской фигуры равна геометрической суше скорости полюса и скорости от вращения фигуры вокруг полюса, т.е.:

,

где , V_BA=ω·AB.

Ускорения точек находятся по теореме об ускорениях: ускорение точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса, т.е.:

,

где ускорение от вращения складывается из нормального и касательного:

Причем направлено к полюсу А и _, , .

При определении скоростей удобно использовать свойства мгновенного центра скоростей (МЦС) и теорему о проекциях скоростей. Напомним, что МЦС - такая точка плоской фигуры, скорость которой равна нулю в данный момент времени. Теорема о проекциях скоростей состоит в том, что проекции скоростей двух точек плоской фигуры на проходящую через эти точки ось равны.

ПРИМЕР 7.1

В механизме, изображенном на рис.7.1, длины стержней равны: l₁=0,4м, l₂=1,2м, l₃=1,4м, l₄=0,6м. Заданы угловая скорость и угловое ускорение кривошипа I: ω₁=5с^-1, ε₁=3с^-1. Нужно найти V_В, а_В - скорость и ускорение точки В, ε_АВ –угловое ускорение стержня АВ, V_E- скорость стержня E, ω_DE- угловую скорость стержня DE [3].

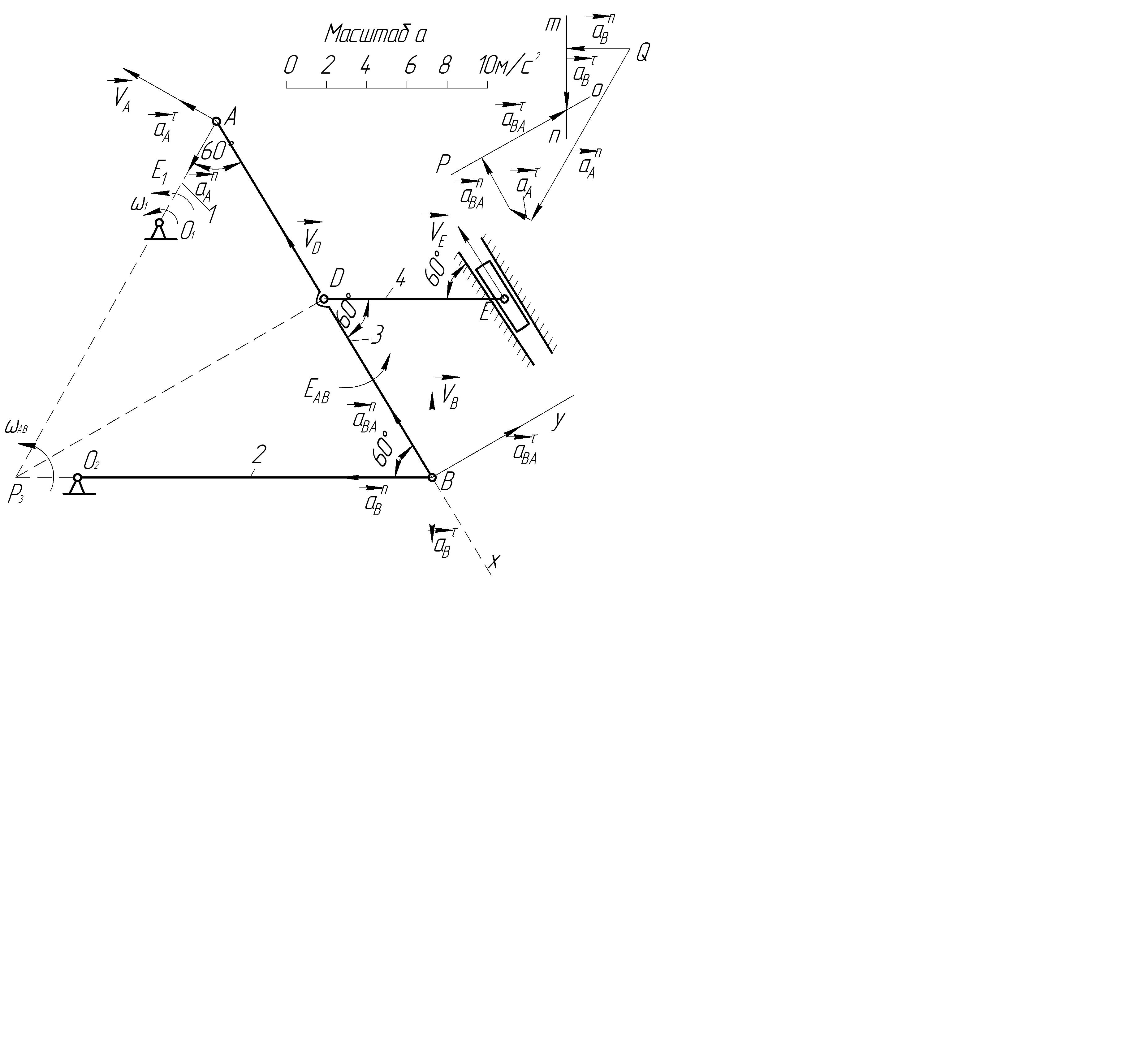
Рис.7.1.

Решение:

Определим скорости. Кривошип I совершает вращательное движение вокруг центра О₁.

Поэтому V_A=ω₁l₁=2м/с. Скорость .

Кривошип 2 также совершает вращательное движение, поэтому Кроме того, точки А и В принадлежат одному стержню АВ. направлена так, чтобы проекции и на АВ имели одинаковую величину и знак. По теореме о проекциях , т.е. м/c.

Чтобы найти V_Е, найдем сначала скорость точки D. Построим МЦС Р₃ стержня АВ_, проведя перпендикуляры к и . Тогда и направлена так, чтобы ее проекция на AB имела одинаковый знак с проекцией . Так как равносторонний, то P₃A=AB=l₃ и угловая скорость стержня АВ:

Из находим .

Тогда

Так как точка E принадлежит ползуну, ее скорость направлена вдоль направляющих ползуна, причем так, чтобы проекции и на DE имели одинаковые знаки. Получаем что , а по теореме o проекциях скоростей V_E cos60°=V_D cos60°, т.е. V_E=V_D= м/с.

Перпендикуляры к скоростям и не пересекаются, у стержня DЕ нет МЦС, значит в данный момент времени стержень DE движется поступательно и ω_Е=0.

Находим ускорения. Так как точка А принадлежит кривошипу I, совершающему вращательное движение, то , причем:

, .

Нормальное ускорение точки А направлено к оси вращения - к точке О₁, касательное ускорение А и направлено по ходу углового ускорения . Точка В движется по окружности радиуса О₂B. Поэтому . Нормальное ускорение точки В имеет величину и направлено к центру вращения О₂ Карательное ускорение точки В . Укажем его предположительное направление на чертеже, так как его действительное направление неизвестно.

Но точка В принадлежит также стержню АВ. Приняв за полюс точку А, получим , или

+ (7.1)

Найдем нормальное ускорение точки В во вращательном движении стержня АВ вокруг полюса А:

Вектор направлен от В к А. Касательное ускорение точки В от вращения стержня АВ вокруг полюса A , укажем на чертеже его предположительное направление.

Таким образом, вектора , известны по величине и направлению, у векторов , известно только направление, т.е. векторное равенство содержит две неизвестные скалярные величины. Но векторное равенство эквивалентно двум скалярным, которые получим, спроектировав его на оси координат х, у:

, (7.2)

(7.3)

Ось X проведена перпендикулярно вектору , поэтому в уравне­ние проекций на ось X входит только неизвестная .

Из уравнения (7.2) находим :

м/с².

Из уравнения (7.3) находим :

м/с².

Теперь находим м/с².

Так как , то _.

Поскольку , а , то действительное направление векторов и совпадает с показанным на рисунке. Направление соответствует направлению , укажем его на чертеже.

Проверим правильность решения задачи, решив уравнение (7.1) геометрически. Для этого от некоторой точки Q отложим в некотором масштабе вектор (рис.7.1). Через его конец проведем прямую . Вдоль этой прямой направлен вектор . Теперь из точки Q отложим вектор . Из конца вектора проведем . От конца вектора отложим вектор . Через конец вектора проводим прямую , вдоль которой направлен вектор . Точка пересечения прямых pq и mn дает концы векторов и . Измеряя эти вектора и учитывая масштаб, получаем =3,1м/с², =4,8м/с², что почти совпадает с аналитическим решением.

ПРИМЕР 7.2

Кривошип О₁А вращается вокруг оси О₁ с постоянной угловой скоростью . Для заданного положения механизма построить мгновенные центры скоростей шатунов АВ и ДЕ, найти скорости точек А, В, Д, Е, угловые скорости указанных шатунов и кривошипа О₂В, а также ускорение точки В (рис.7.2.1) [3].

Размеры звеньев: О₁А=l₁=0,6 м; AB=l₂=1,5 м; ДЕ=l₃ =1,2м; О₂В=l₄=0,6м, АД=ДВ.

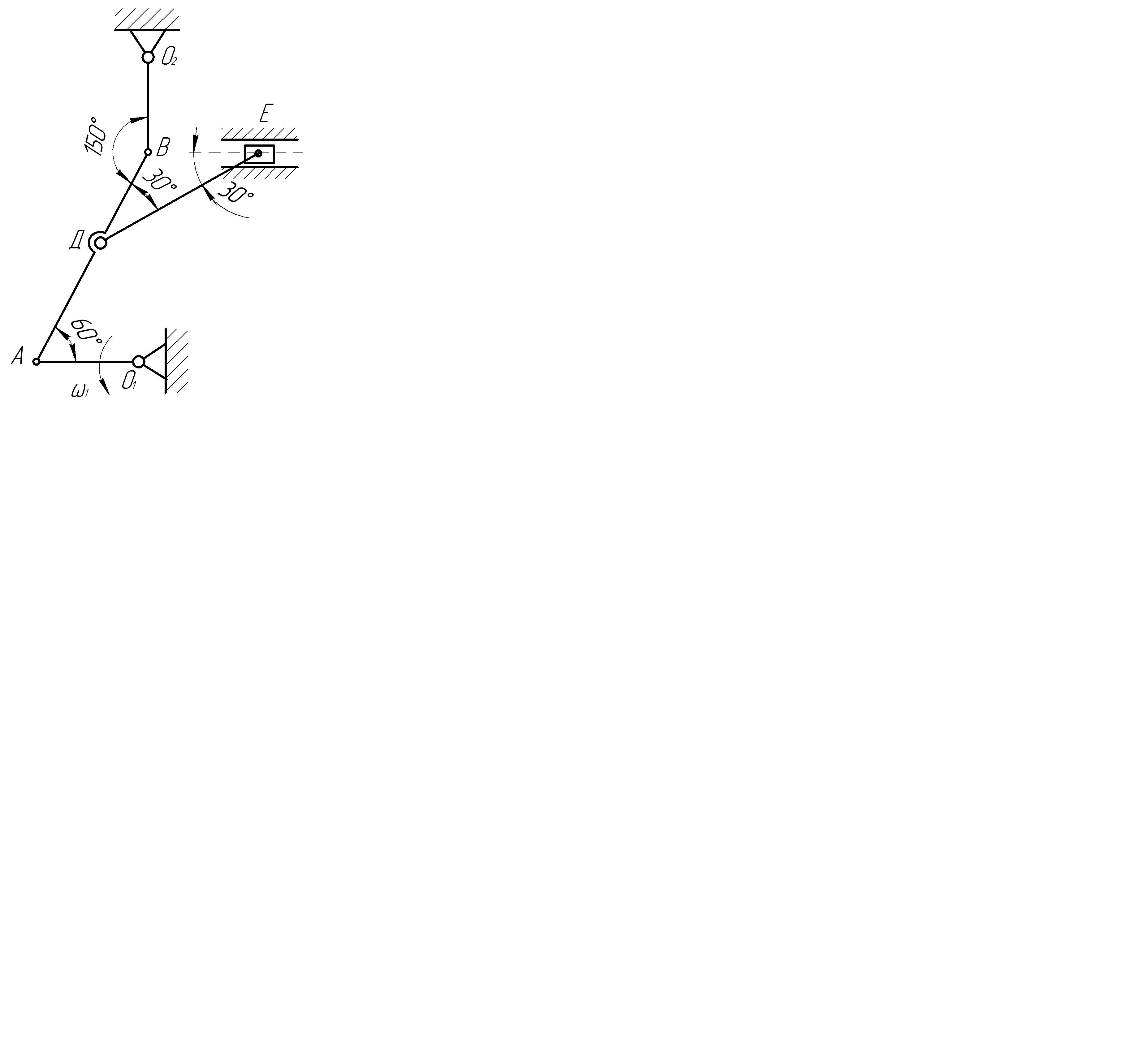
Рис.7.2.1.

Решение:

Звенья О₁А и О₂В механизма совершают вращательное дви­жение; звенья АВ и ДЕ совершают плоскопараллельное движение.

Скорость точки А звена О₁А:

Находим положение мгновенного центра скоростей (МЦС) звена АВ (точки Р_АВ) рис.7.2.2. Очевидно, что . Проводим и . Точка Р_АВ - МЦС звена АВ.

Угловая скорость звена АВ:

с^-1,

где м.

Скорость точек Д и В звена АВ:

где ДР_АВ=АД=0,5АВ=0,5l₂=0,75м;

ВР_АВ=АВcos30⁰=l₂cos30⁰=1,3м.

Находим МЦС звена ДЕ (точки Р_ДЕ). Для этого восстановим перпендикуляры и в точке Д ,Е и найдем точку пересечения этих перпендикуляров Р_ДЕ. Вычисляем угловую скорость этого звена:

где ДР_ДЕ=ДЕtg60⁰=l₃tg60⁰=1,2 ≈2,08м.

Скорость точки Е звена ДЕ:

где м.

Угловая скорость звена О₂В:

Ускорение точки А звена О₁А:

,

где м/с²;

; ; ;

м/с².

Для определения ускорения точки В воспользуемся векторной формулой , или:

(7.2.1)

Изображаем векторы ускорений, входящих в эту векторную форму­лу, на схеме механизма (см. рис. 7.2.2).

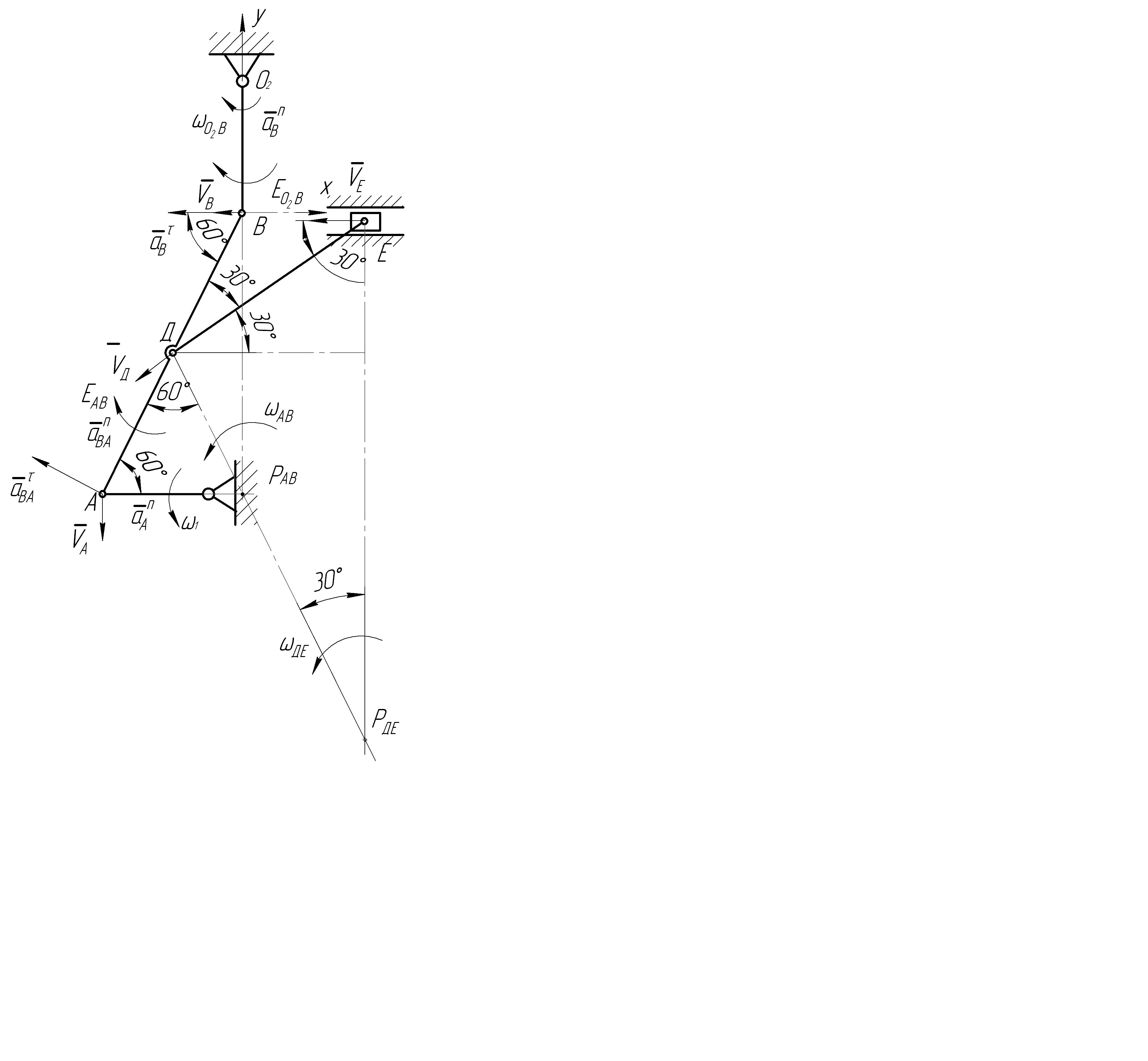
Рис.7.2.2.

Вычисляем ускорения и :

м/с²;

Проектируя обе части векторной формулы (7.2.1) на оси координат Вху, получаем:

(7.2.2)

Из системы уравнений (7.2.2) находим ускорения и :

м/с²; м/с.

Угловые ускорения звеньев АВ и О₂В соответственно:

;

.

Ускорение точки В:

.

ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ

Задание К 1

Определение скорости и ускорения точки по заданным уравнениям

ее движения

К-I, в.I

Найти уравнение траектории, а также определить скорость и ускорение точки в момент пересечения ею оси у, если уравнения движения ее заданы: ; (х, у - в см, t - в с.)

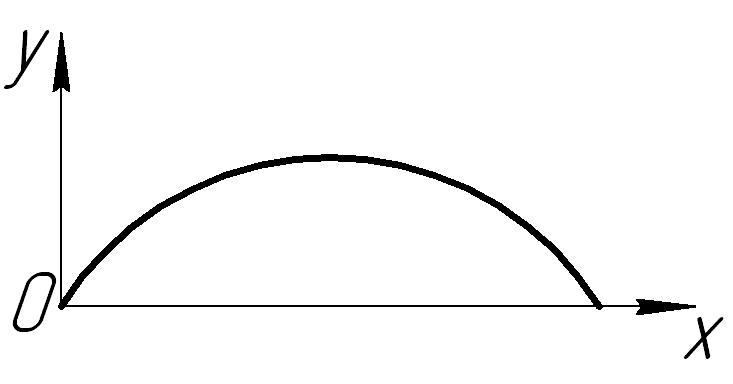
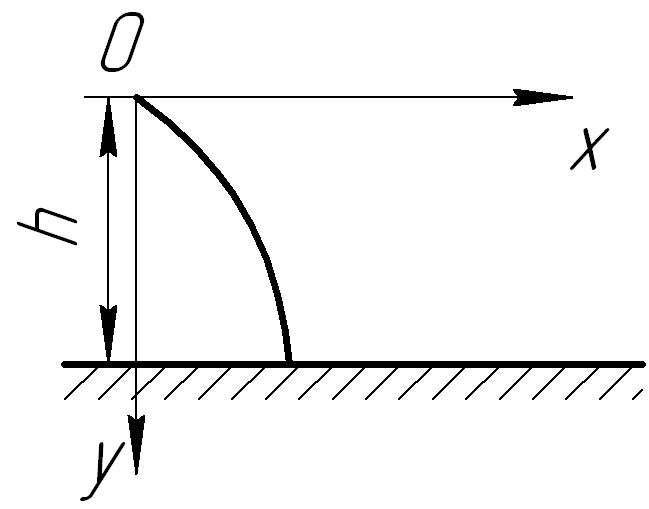
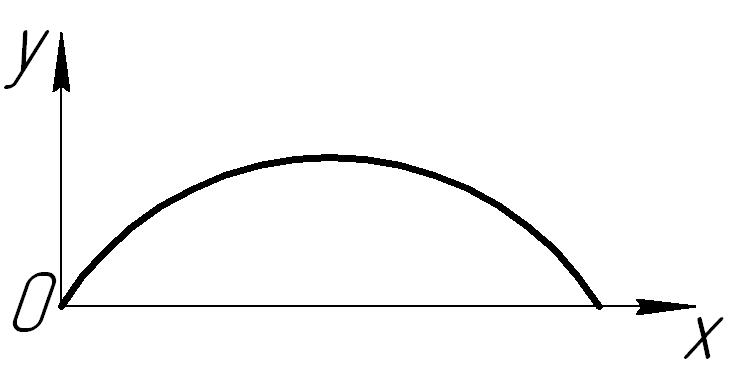
	К-I, в.2 Движение снаряда определяется уравнениями: , (х, у - в м, t - в с.). Найти уравнение траектории, время и дальность полета снаряда, а также начальную скорость.
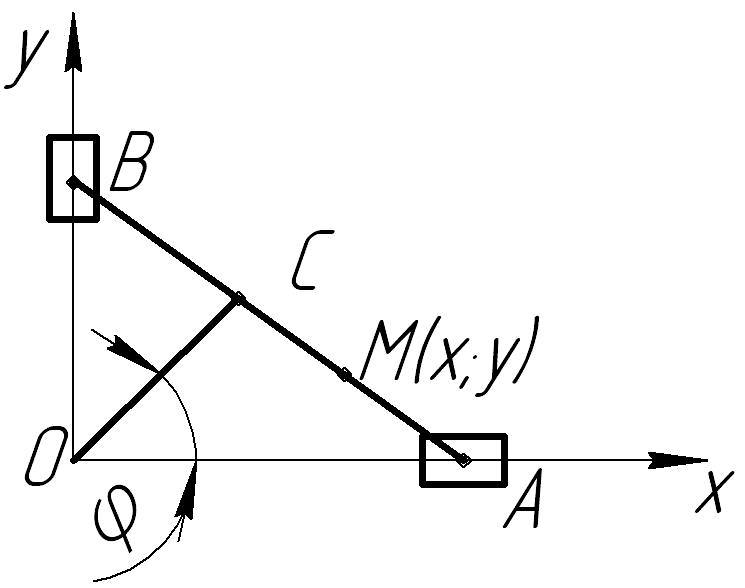
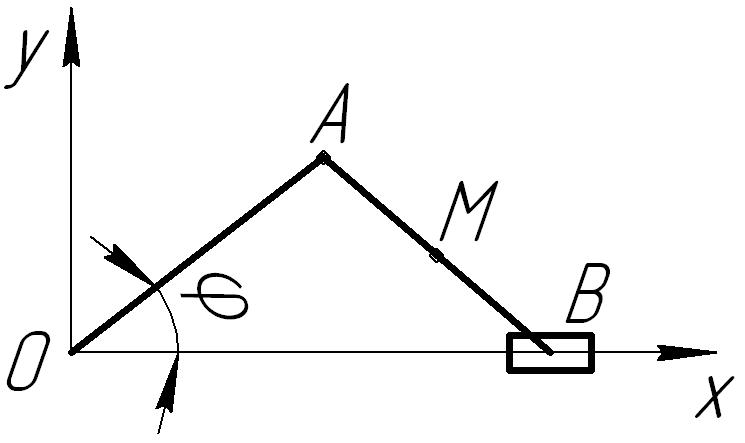
	К-I, в.3 Дано: АВ=80 см, ОС=43 см, АС=ВС, АМ=15 см, . Найти уравнение траектории, скорость и уравнение годографа скорости точки М.

К-I, в.4

Найти уравнение траектории, а также определить скорость и ускорение точки в момент пересечения ею оси х, если уравнения движения ее заданы: ; (х, у - в см, t - в с.)

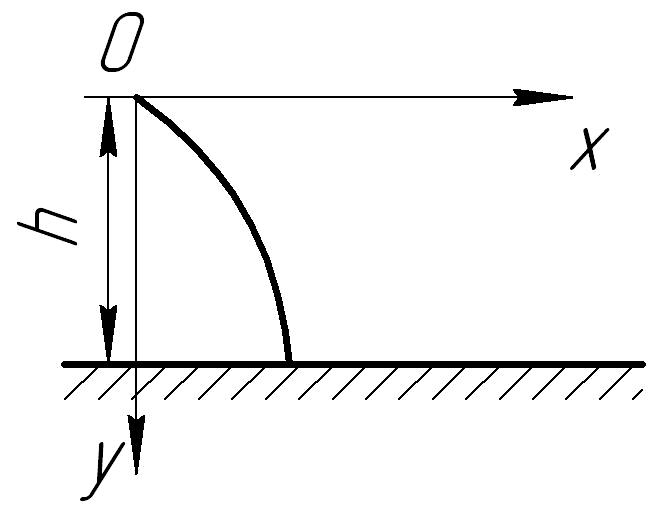
	К-I, в.5 Движение груза задано уравнениями ; (х, у - в м, t - в с.). Найти уравнение траектории, дальность полета по горизонтальному направлению, время падения и начальную скорость, если самолет летит на высоте h=2500м. Начало координат взято в точке сброса.
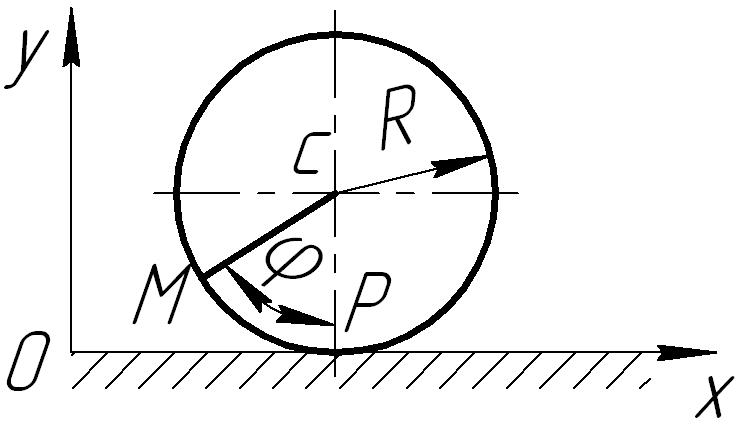
	К-I, в.6 Дано: R=650см; ; ; Для точки M составить уравнения движения и для момента . Найти скорость и ускорение.

К-I, в.7

Уравнения движения точки: ; (х, у - в см, t – в с.). Найти уравнение траектории точки, а также ее скорость и ускорение в момент времени, когда скорость параллельна оси х.

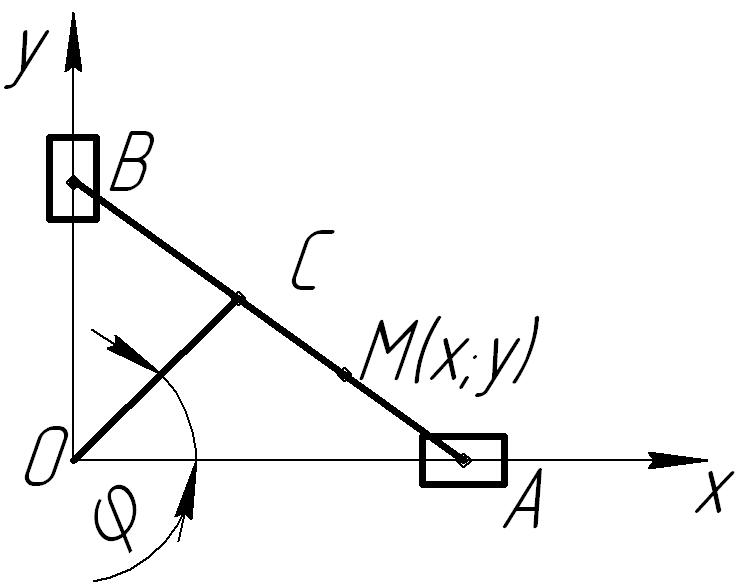
К-I, в.8 Определить уравнение траектории, скорость и ускорении середины (точка M) шатуна, если ОА=АВ=4а; .

К-I, в.9

Найти уравнение траектории точки, а также ее скорость и ускорение в момент времени, когда скорость параллельна оси y, если уравнения ее движения заданы: ; (х, у - в м, t - в с.).

К-I, в.10

Найти уравнение траектории, а также определить скорость и ускорение точки в момент пересечения ею оси y, если уравнения движения ее заданы: ; . (х, у - в см, t - в с.).

	К-I, в.11 Дано: АВ=70 см, ОС=35 см, АС=ВС, АМ=15 см, . Найти уравнение траектории, скорость и уравнение годографа скорости точки М.
	К-I, в.12 Дано: АВ=86 см, ОС=45 см, АС=ВС, АМ=25 см, . Найти уравнение траектории, скорость и уравнение годографа скорости точки М.

К-I, в.13

Найти уравнение траектории, а также определить скорость и ускорение точки в момент пересечения ею оси х, если уравнения движения ее заданы: ; (х, у - в м, t - в с.).

К-I, в.14

Найти уравнение траектории, а также определить скорость и ускорение точки в момент пересечения ею оси х, если уравнения движения ее заданы: ; (х, у - в м, t - в с.).

	К-I, в.15 Движение груза задано уравнениями ; (х, у - в м, t - в с.). Найти уравнение траектории, дальность полета по горизонтальному направлению, время падения и начальную скорость, если самолет летит на высоте h=3625м. Начало координат взято в точке сброса.
	К-I, в.16 Дано: АВ=30 см, ОС=15 см, АС=ВС, АМ=10 см. Найти уравнение траектории, скорость и уравнение годографа скорости точки М.
	К-I, в.17 Определить уравнение траектории, скорость и ускорении середины (точка M) шатуна, если ОА=АВ=6а; .
	К-I, в.18 Определить уравнение траектории, скорость и ускорении середины (точка M) шатуна, если ОА=АВ=6а; .

К-I, в.19

Найти уравнение траектории точки, а также ее скорость и ускорение в момент времени, когда скорость параллельна оси y, если уравнения ее движения заданы: ; (х, у - в м, t - в с.).

К-I, в.20

Найти уравнение траектории точки, а также ее скорость и ускорение в момент времени, когда скорость параллельна оси y, если уравнения ее движения заданы: ; (х., у - в м, t - в с.).

	К-I, в.21 Движение груза задано уравнениями ; (х, у - в м, t - в с.). Найти уравнение траектории, дальность полета по горизонтальному направлению, время падения и начальную скорость, если самолет летит на высоте h=2125м. Начало координат взято в точке сброса.
	К-I, в.22 Дано: R=250см; Y=2πt; ; Для точки M составить уравнения движения и для момента . Найти скорость и ускорение.
	К-I, в.23 Дано: R=70см; Y=πt; ; Для точки M составить уравнения движения и для момента . Найти скорость и ускорение.

К-I, в.24

Уравнения движения точки: ; (х, у - в см, t - в с.). Найти уравнение траектории точки, а также ее скорость и ускорение в момент времени, когда скорость параллельна оси х.

К-I, в.25

Уравнения движения точки: ; (х, у - в см,

t–в с.). Найти уравнение траектории точки, а также ее скорость и ускорение в момент времени, когда скорость параллельна оси х.

К-I, в.26

Найти уравнение траектории, а также определить скорость и ускорение точки в момент пересечения ею оси y, если уравнения движения ее заданы: ; (х, у - в см, t - в с.).

К-I, в.27

Найти уравнение траектории, а также определить скорость и ускорение точки в момент пересечения ею оси y, если уравнения движения ее заданы: ; (х, у - в см, t - в с.).

	К-I, в.28 Движение снаряда определяется уравнениями: , (х, у - в м, t - в с.). Найти уравнение траектории, время и дальность полета снаряда, а также начальную скорость.
	К-I, в.29 Движение снаряда определяется уравнениями: , (х, у - в м, t – в с.). Найти уравнение траектории, время и дальность полета снаряда, а также начальную скорость.
	К-I, в.30 Движение снаряда определяется уравнениями: , (х, у - в м, t – в с.). Найти уравнение траектории, время и дальность полета снаряда, а также начальную скорость.