Необходимые данные:

Таблица 6.5.1

, рад	Расстояние, см.				Длина звеньев, см.
	A	b	c	d	О1А	О2В	О3D	АВ	ВС	СD	СЕ	ЕF
140	71	27	32	40	16	30	50	46	33	40	20	50

Решение:

Изображаем положение механизма согласно данных (рис.6.5.1).

Вводим масштабный коэффициент по длинам:

Рис. 6.5.1. Механизм с указанием направлений скоростей всех точек

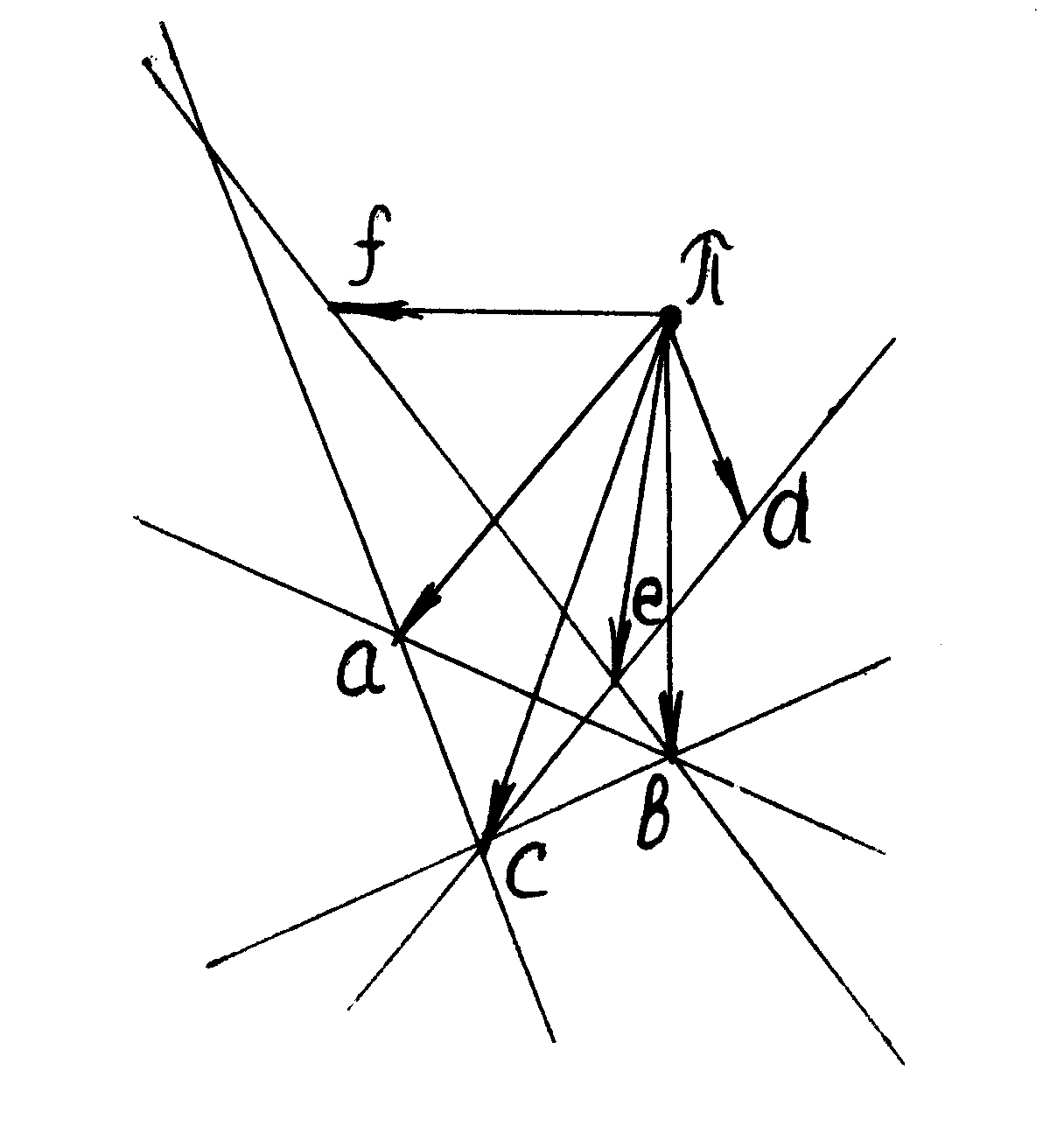
Рис. 6.5.2. План скоростей

Определяем скорости точек механизма и угловые скорости звеньев с помощью плана скоростей (рис.6.5.2).

Точка А принадлежит кривошипу О₁А, который совершает вращательное движение, поэтому:

Вектор V_А направлен перпендикулярно кривошипу О₁А в сторону .

Введем масштабный коэффициент по скоростям:

Для определения скорости точки В строим план скоростей согласно векторному уравнению:

.

Для этого из произвольно выбранного полюса  проводим луч Оа , в выбранном масштабе скорость точки А. Затем через конец вектора V_А проводим направление , перпендикулярно звену АВ, а из полюса  проводим направление скорости перпендикулярно звену О₂В. На пересечении этих направлений получаем точку в, отрезок в определяет скорость точки В. Измеряем длину луча в и, пользуясь масштабным коэффициентом по скоростям, получаем:

.

Так как , то конец вектора будет находиться на пересечении направлений векторов скоростей .

Вектор скорости направлен перпендикулярно СА, вектор направлен перпендикулярно СВ. Пересечение этих направлений происходит в точке С.

Измерив отрезок с определим:

С помощью векторного уравнения определяем скорость , учитывая что вектор скорости направлен перпендикулярно DC, .

Из соотношения определяем , а затем

Для определения составим векторное уравнение , построим это векторное уравнение на плане скоростей, определив f.

Определяем угловые скорости всех звеньев:

Определяем скорость точек механизма и угловое скорости звеньев с помощью мгновенных центров скоростей (рис.6.5.3)

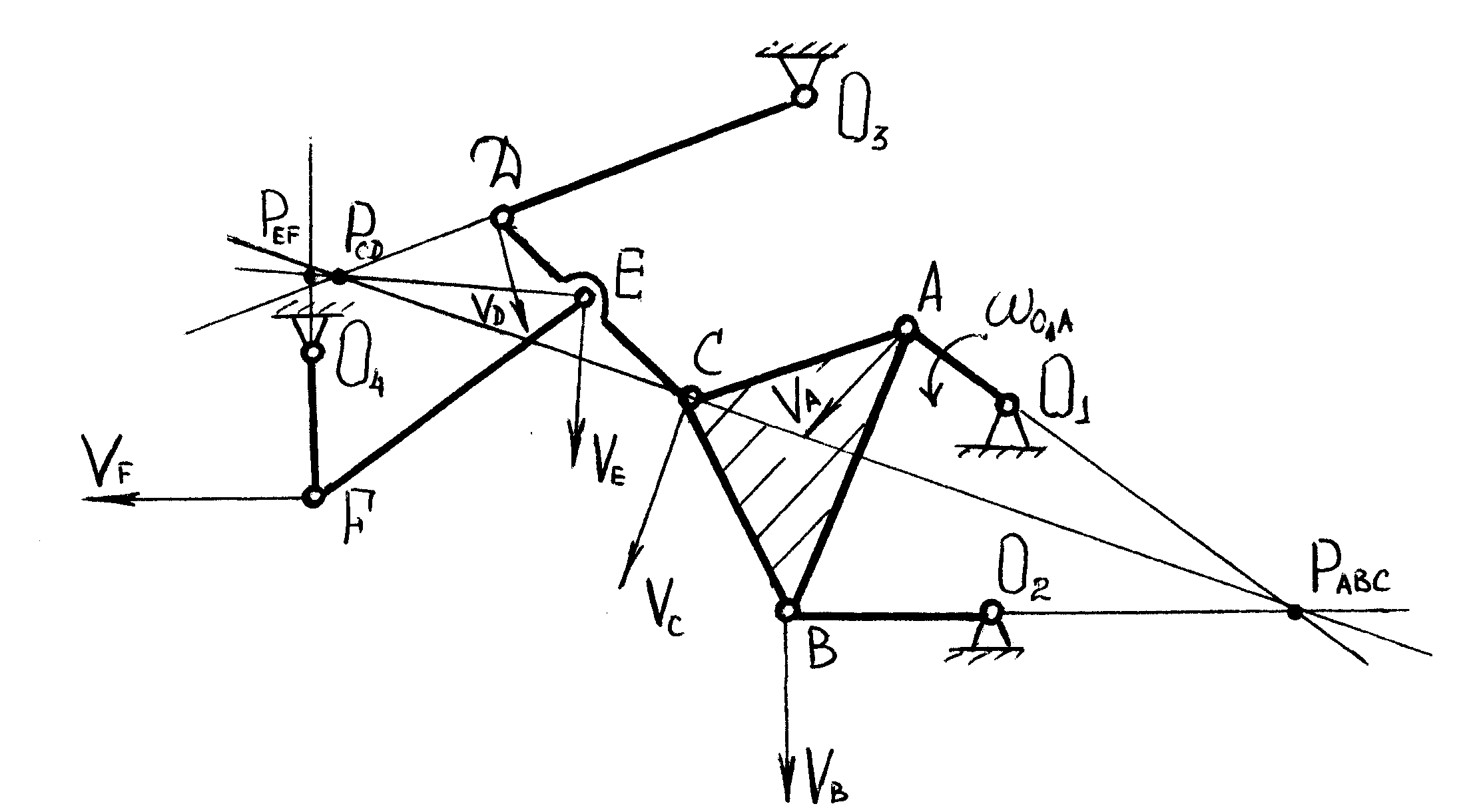
Рис. 6.5.3. Построение мгновенных центров скоростей

для звеньев механизма.

Определяем условие скорости звеньев:

Полученные результаты сводим в таблицу 6.5.2

Таблица 6.5.2

Способ определения	Скорость точек, см/с						Угловые скорости звеньев, рад./с
	VА	VВ	VС	VD	VE	VF	ABC	BO2	CD	EF	O4F	O5F
План скоростей	32	29	38	9	20,5	25,5	0,57	0,96	0,81	0,58	1,27	0,18
С помощью МЦС	32	30	39	8,6	21	25,8	0,55	1	0,84	0,58	1,29	0,17

Определяем ускорение точек А и В, а также угловое ускорение звена АВ Для этого выделим часть механизма содержащую звено АВ (рис.6.5.4).

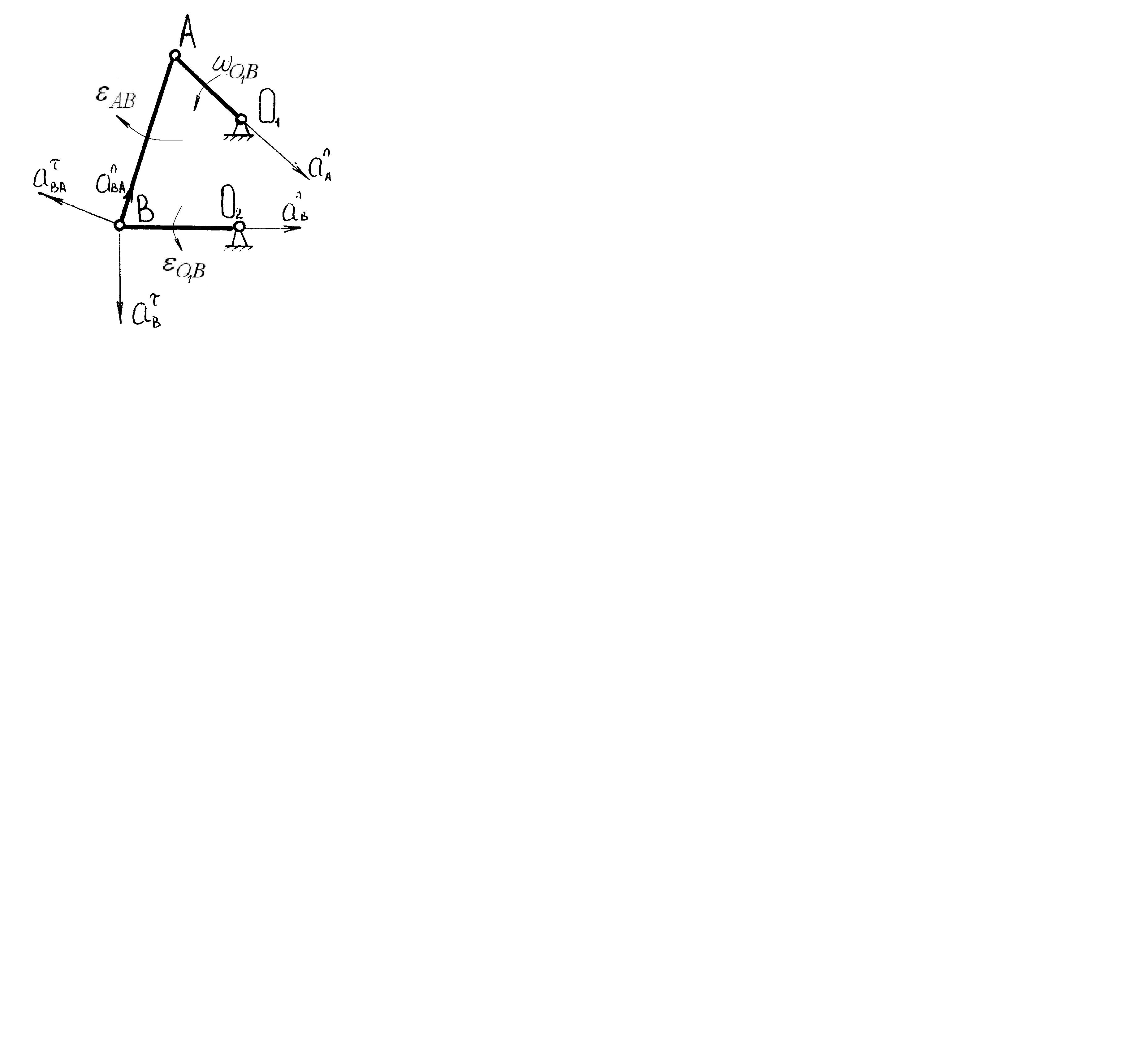
Рис.6.5.4.. Часть механизма с указанием направлений

характерных ускорений

Рис.6.5.5. План ускорений

Составим векторное уравнение:

Кривошип О₁А вращается равномерно, ускорение точки А направлено к центру О₁ и равно:

Вектор направляется от точки А к центру вращения О₁. Центростремительное ускорение точки В во вращательном движении шатуна АВ направлено от точки В к точке А и равно:

Центростремительное ускорение точки В во вращательном движении шатуна О₂В направлено от точки В к точки О₂ и равно

Ускорения и определить невозможно, но известны направления этих ускорений: направлено перпендикулярно АВ, а вектор направлен перпендикулярно О₂В.

Для определения величины и строим план ускорения. Введем масштабный коэффициент по ускорениям:

Из плана ускорений (рис. 6.25) с учетом масштабного коэффициента определяем:

С помощью полученных данных определяем угловые ускорения звеньев (рис. 6.5.4):

Определяем положение мгновенного центра ускорения звена АВ (рис. 6.5.6.)

Рис.6.5.6. Построение мгновенного центра ускорений

Примем точку А за полюс. Тогда ускорение точки В равно:

Строим параллелограмм ускорений точке В по диагонали и стороне Сторона параллелограмма выражает ускорение точки В во вращении АВ вокруг полюса А. Ускорение составляет с отрезком АВ угол , который можно измерить на чертеже.

Направление вектора относительно полюса А позволяет определить направление , в данном случае соответствующее направлению вращения часовой стрелки. Отложив угол от векторов и в этом направлении и проведя две полупрямые, найдем точку их пересечения Q_AB – мгновенный цент ускорений звена АВ.