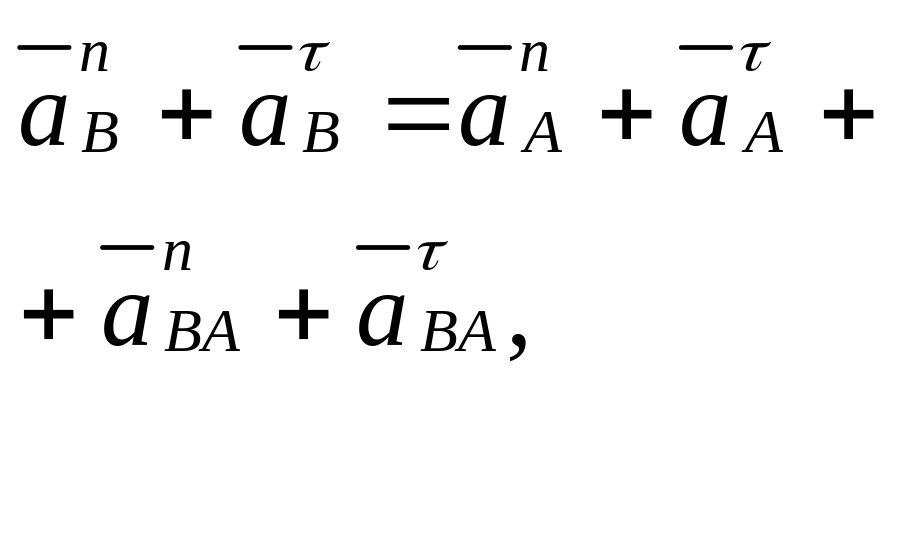IV плоское движение твердого тела

4.1 Кинематический расчет плоского механизма

4.1.1 Скорость точек плоского механизма

Для определения скоростей точек при плоскопараллельном движении применяются два способа:

1. с помощью мгновенного центра скоростей – аналитический;

2. с помощью плана скоростей - графический.

Мгновенный центр скоростей – это точка, лежащая на пересечение перпендикуляров, проведенных к векторам скоростей. Величина скорости МЦС в данный момент времени равна нулю. Скорость точки этим способом определяется как произведение угловой скорости звена, которому принадлежит точка, на расстояние от этой точки до мгновенного центра скоростей:

.

План скоростей строится в соответствии с векторной суммой:

согласно которой скорость любой точки ( ) плоского механизма равна векторной скорости точки, принятой за полюс ( ), и скорость этой точки вокруг полюса( ).

За полюс выбираем точку, скорость которой либо задается, либо сразу определяется.

Скорость направляется перпендикулярно звену, которому принадлежат эти точки: перпендикулярно АВ [1].

7.1.2 Определение ускорений плоского механизма

При определении ускорения точек плоского механизма следует помнить, что при движении точки по траектории в виде окружности ускорение необходимо разложить на две составляющие и определить каждую по формуле (рис.4.2.2.1):

При движении точки по прямой (см. движение ползуна в механизмах) им имеет место только одно ускорение (без разложения на составляющие) (рис. 4.2.2.1)

Рис.4.2.2.1

Задача k-6. Определение скоростей точек твердого тела при плоском движении

Найти для заданного положения механизма скорости точек А, В, С и угловые скорости всех звеньев, если известна угловая скорость кривошипа [2]_.

ПРИМЕР 6.1

Дано: 1) схема механизма в заданном положении рис. 6.1

2) исходные данные. Таблица 6.1

Таблица 6.1

Размеры, см				ωOA c-1
ОА	АВ	ВС	r
40	80	25	15	2

Решение: Скорость точки А направлена перпендикулярно к кривошипу ОА. Ее модуль:

cм/с.

Скорость центра В колеса направлена по горизонтали. Находим для звена АВ мгновенный центр скорости Р_АВ, восставив перпендикуляры к скоростям точек А и В.

Угловую скорость звена АВ определяем по формуле:

Как видно из рисунка:

см.

Следовательно,

см;

см;

с^-1.

Скорость центра В колеса определяем как вращательную вокруг мгновенного центра скоростей P_AB:

Так как

или

см,

то скорость центра колеса:

см/с.

Мгновенный центр скоростей Р колеса находится в точке касания этого колеса с неподвижном плоскостью.

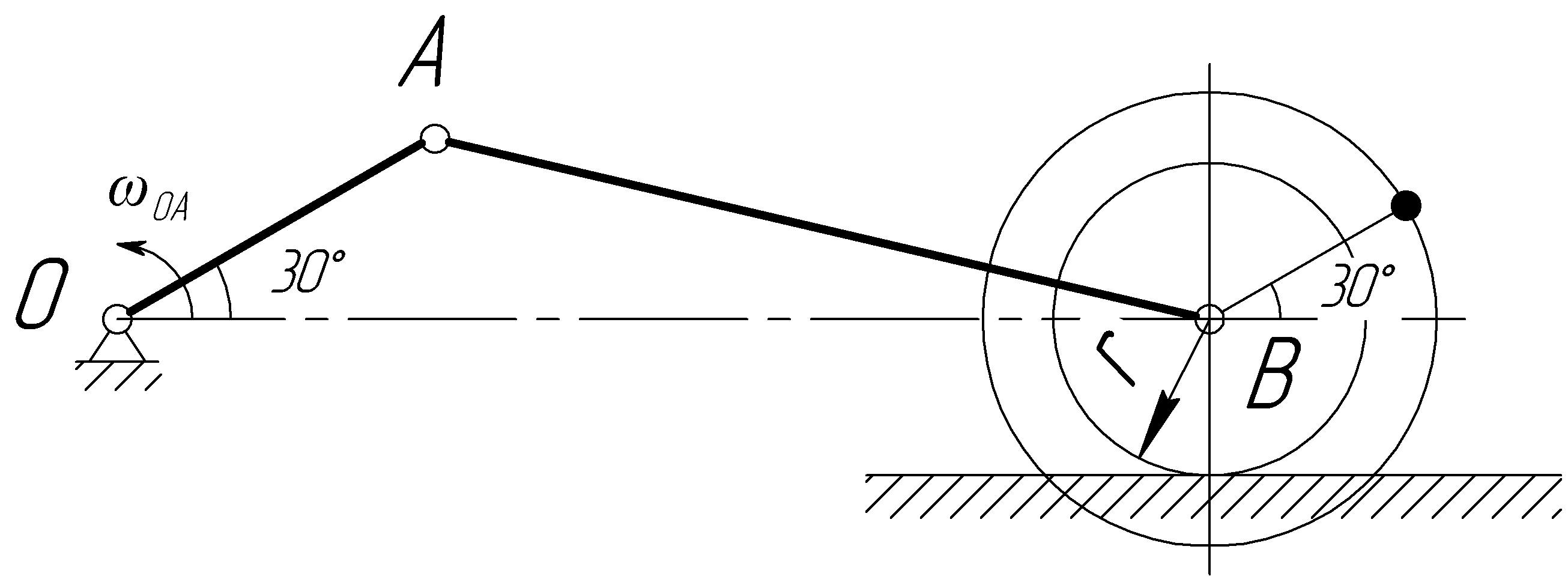
Рис. 6.1

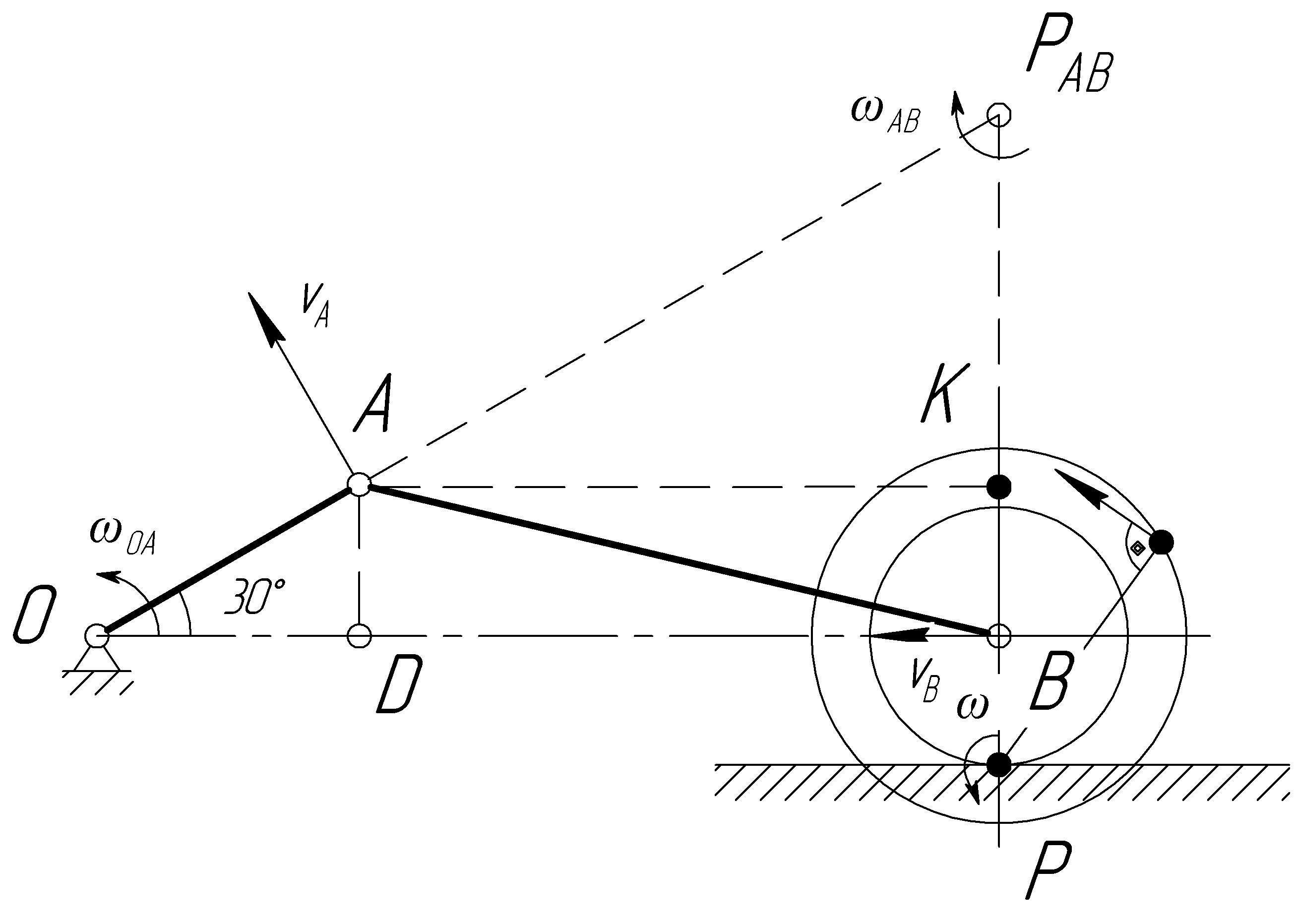
Рис.6.2.

Угловая скорость колеса:

.

Так как ВР=r=15 см, то с^-1.

Скорость точки С определим как вращательную скорость вокруг мгновенного центра скоростей Р:

По теореме косинусов:

или

см.

Следовательно, скорость точки С:

см/с

Вектор направлен перпендикулярно к PC в сторону вращения колеса.

ПРИМЕР 6.2

Для заданного положения механизма рис. 6.2.1 определить скорость точек А и В и угловую скорость звена А В с помощью мгновенного центра скоростей и с помощью построения плана ускорения. Определить ускорения точек А и В, угловое ускорение звена АВ с помощью построения плана ускорения, а также аналитическим методом.

Дано: ОА=35см; АВ=60; ; .

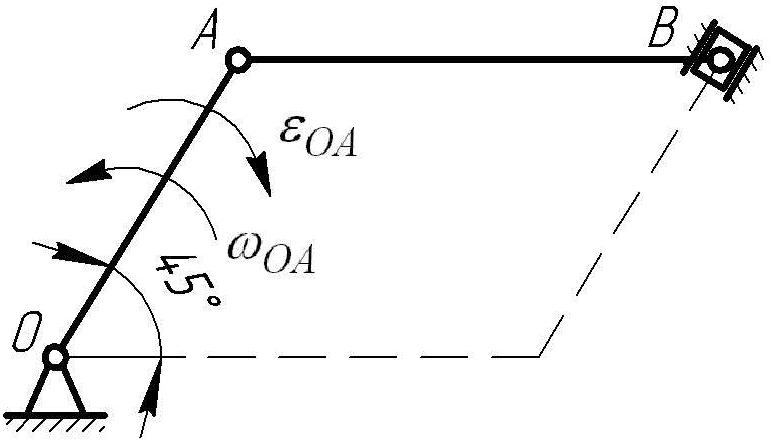
Рис. 6.2.1

Определяем скорость точки А и В с помощью мгновенного центра скоростей. Определяем .

Для определения мгновенного центра скоростей восстанавливаем перпендикуляры в точках А и В к скорости и к линии действия скорости (линия действия направлена по движению ползуна) и находим точку пересечения этих перпендикуляров Р_АВ. Тогда:

(6.2.1)

где, Р_АВ- мгновенный центр скоростей звена АВ (рис.6.2.2).

.

Угловая скорость звена АВ:

Определим скорость точек А и В с помощью плана скоростей.

Составим векторное уравнение принимая точку А за полюс

, (6.2.2)

( направлено перпендикулярно ОА в сторону ). Линия действия направлена перпендикулярно АВ, линия действия направлена по движению ползуна.

Строим треугольник скоростей согласно векторной сумме (6.2.2), см. рис.6.2.3.

Из плана скоростей имеем:

Определяем ускорение точек А и В с помощью построения плана ускорений.

Составим векторное уравнение, принимая точку А за полюс (рис. 6.2.4).

(6.2.3)

Определяем ; ; :

(направлено перпендикулярно ОА в сторону );

(направлено от А к О);

(направлено от В к А).

Линия действия направлена перпендикулярно АВ.

Строим план ускорений (рис. 6.2.5), из которого получаем:

; ; .

Определяем ускорение точек А и В аналитическим способом (проецируем векторную сумму (6.2.3) на оси координат Х, У) рис. 7.3.2.5

Х:

У:

Из первого уравнения получаем:

Из второго уравнения имеем:

Определяем угловое ускорение звена АВ

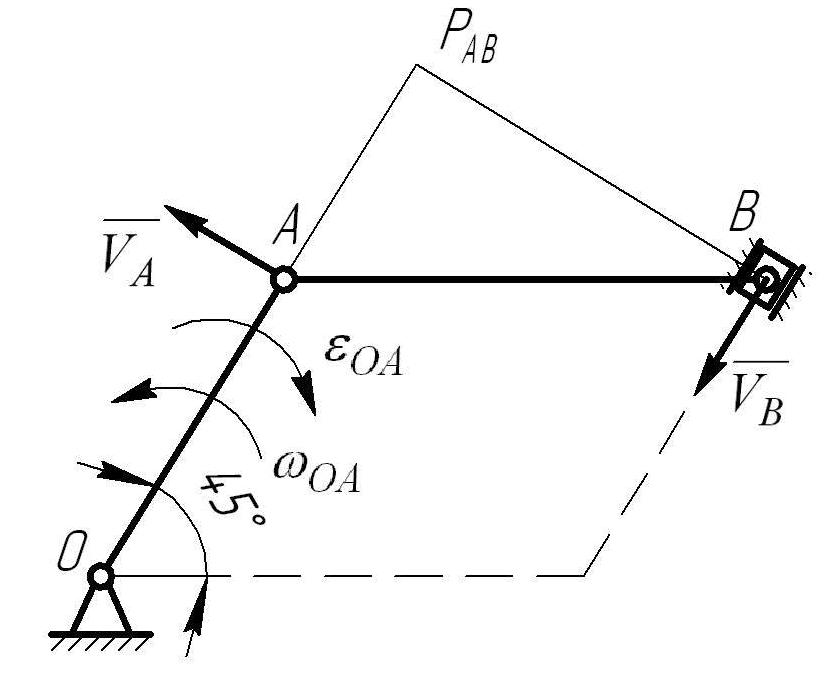
Рис.6.2.2. Схема механизма

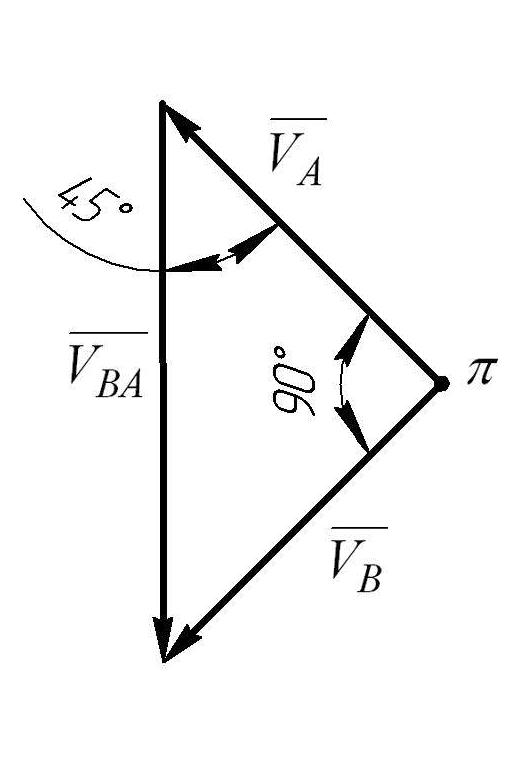
Рис.6.2.3. План скоростей

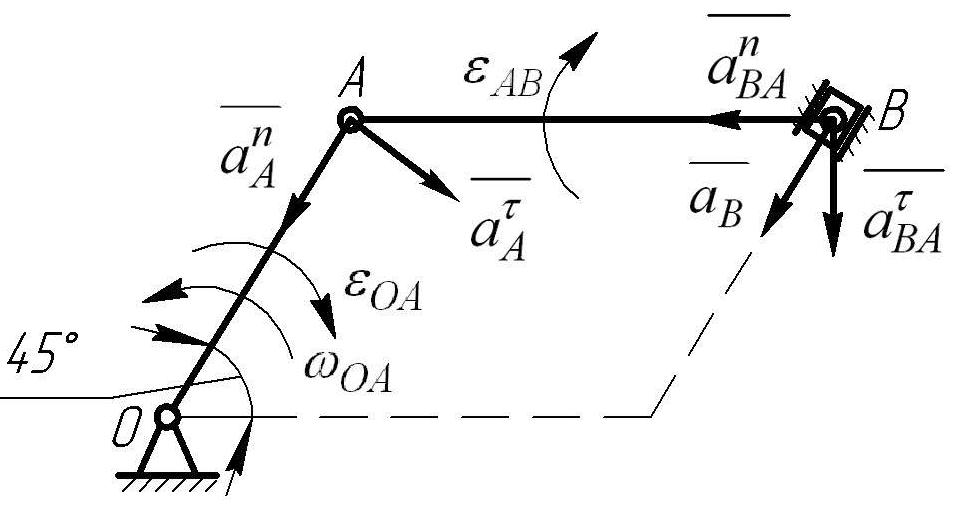
Рис.6.2.4. Схема механизма

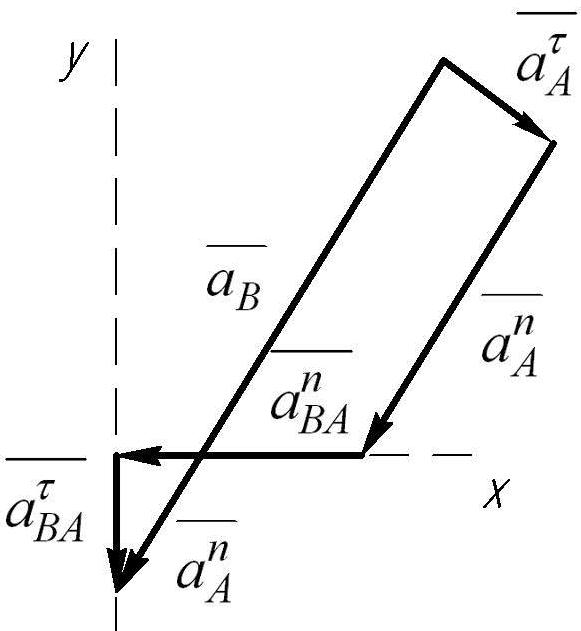
Рис.6.2.5. План ускорения

ПРИМЕР 6.3

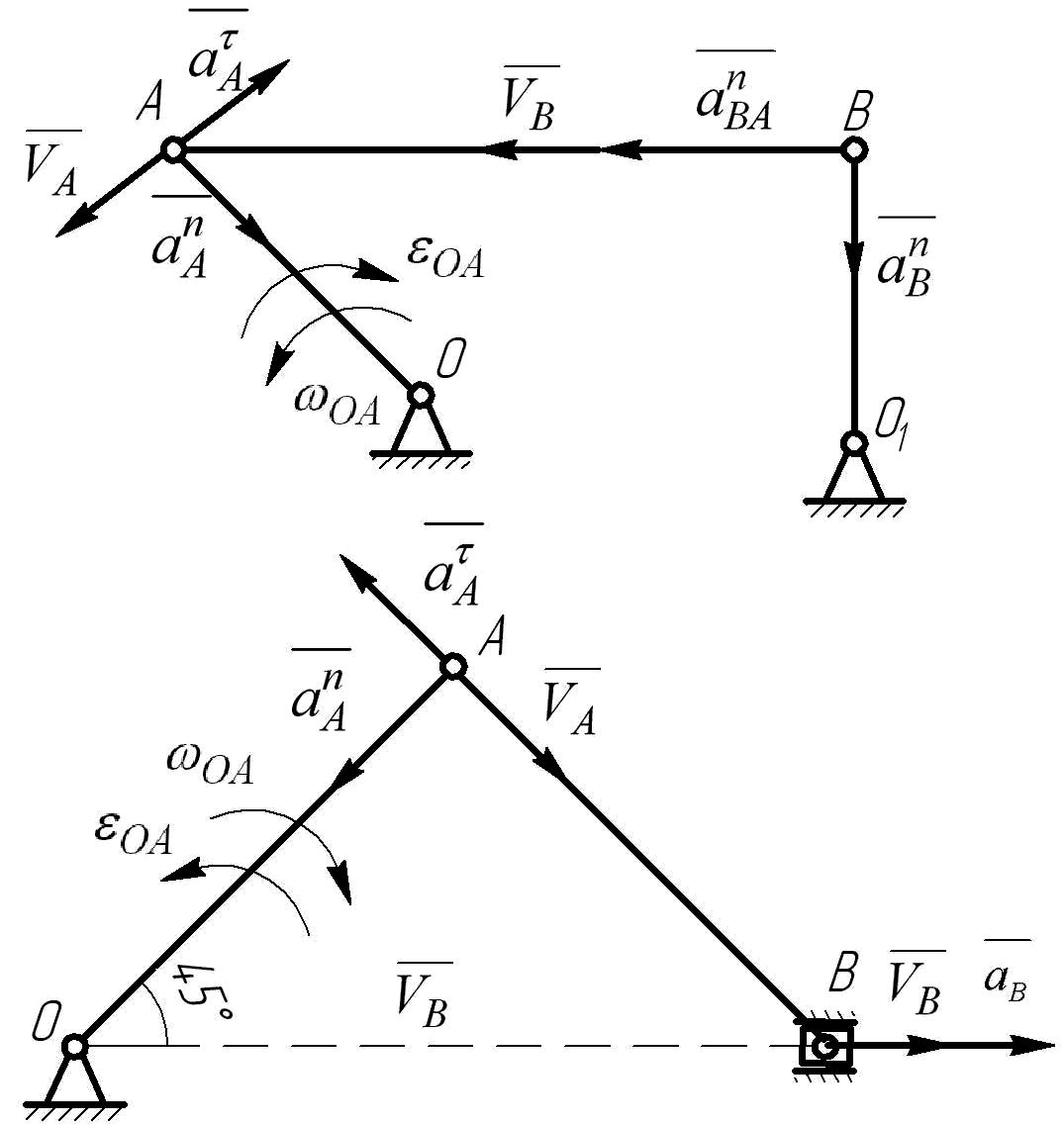
Определить скорость и ускорение точки В заданного механизма, а также угловую скорость и угловое ускорение звена АВ, если:

; .

ОА=2м, АВ=3м, ВО₁=3м (см. рис. 6.3.1а).

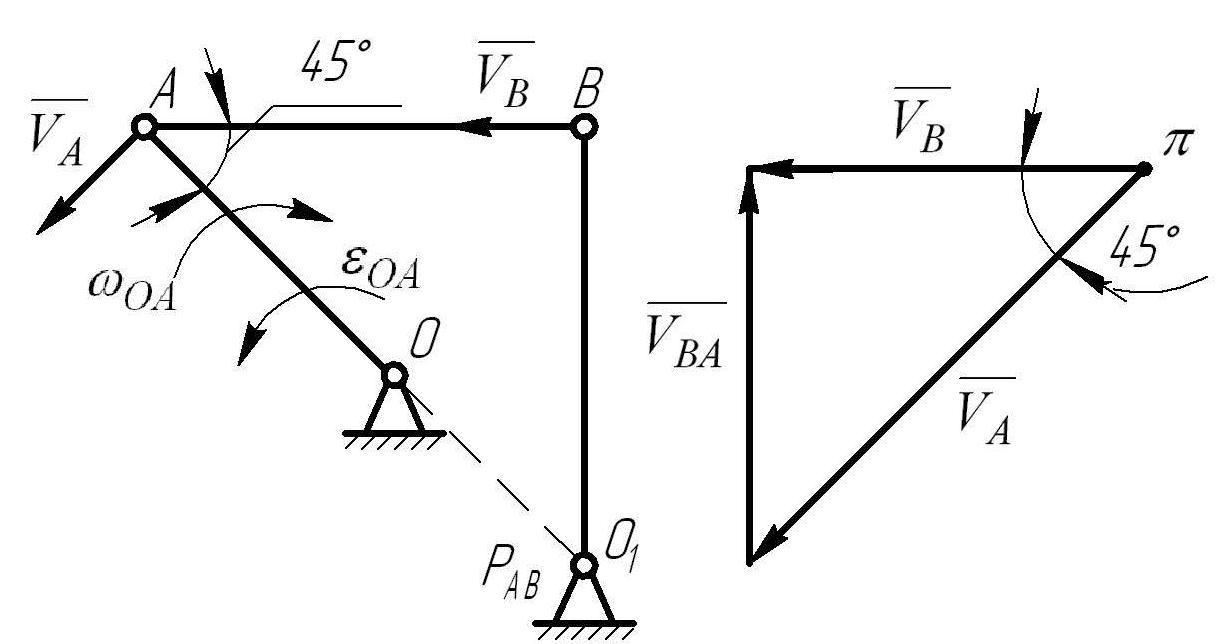
а) б)

Рис.6.3.1(а). Схема механизма и построение МЦС;(б) План скоростей

Решение:

Определим скорость точек А и В и с помощью мгновенного центра скоростей. (рис. 6.3.1 а)

( направлено перпендикулярно ОА в сторону ). Линия действия направлена перпендикулярно О₁В. Строим МЦС и определяем:

Из выражения определяем

Определим скорость точки В с помощью построения плана скоростей. Составим векторное уравнение, принимая точку А за полюс:

(направлена перпендикулярно звену ОА в сторону угловой скорости ω_ОА)_.

Линия действия направлена перпендикулярно АВ,

Вектор скорости направляется перпендикулярно отрезку ВО₁.

Строим план скоростей (рис.6.3.1 б).

Отсюда имеем:

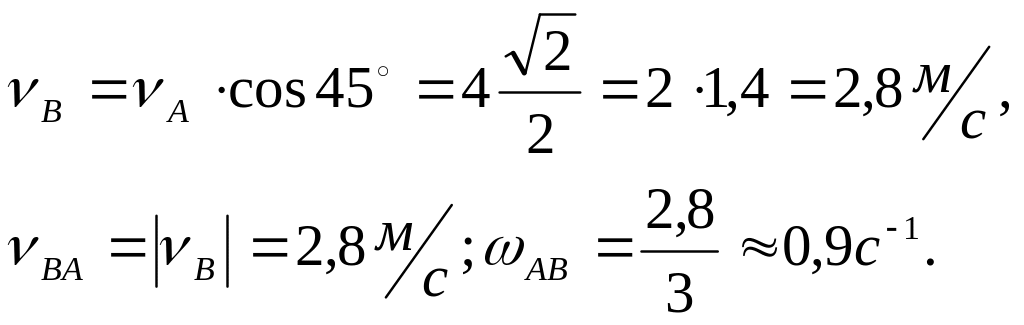
Определяем ускорение точки В с помощью построения плана ускорения, составим векторное уравнение принимая точку А за полюс:

(6.3.1)

(направлено от точки А к центру О (рис. 6.3.2,а)),

(направлено перпендикулярно звену ОА в сторону направления ),

(направлено от точки В по звену АВ к точки А (рис. 6.3.2, а), линия действия направлена перпендикулярно АВ. Определяем: (направлено от В к О₁). Линия действия направлена перпендикулярно .

Строим план ускорений (рис. 6.3.2,б).

С помощью плана ускорений определяем м/с², м/с².

Определяем угловые ускорения звеньев АВ и О₁В:

Для определения направления переносим вектор с плана ускорения на схему в точку В и совершаем кратчайший поворот этого вектора до совмещения со звеном АВ.

Для определения направления углового ускорения переносим вектор с плана ускорения на схему в точку В и совершаем кратчайший поворот этого вектора до совмещения со звеном О₁В.

Определим ускорение и аналитическим способом, спроектировав векторную сумму (6.3.1) на оси координат (рис. 6.3.2 б).

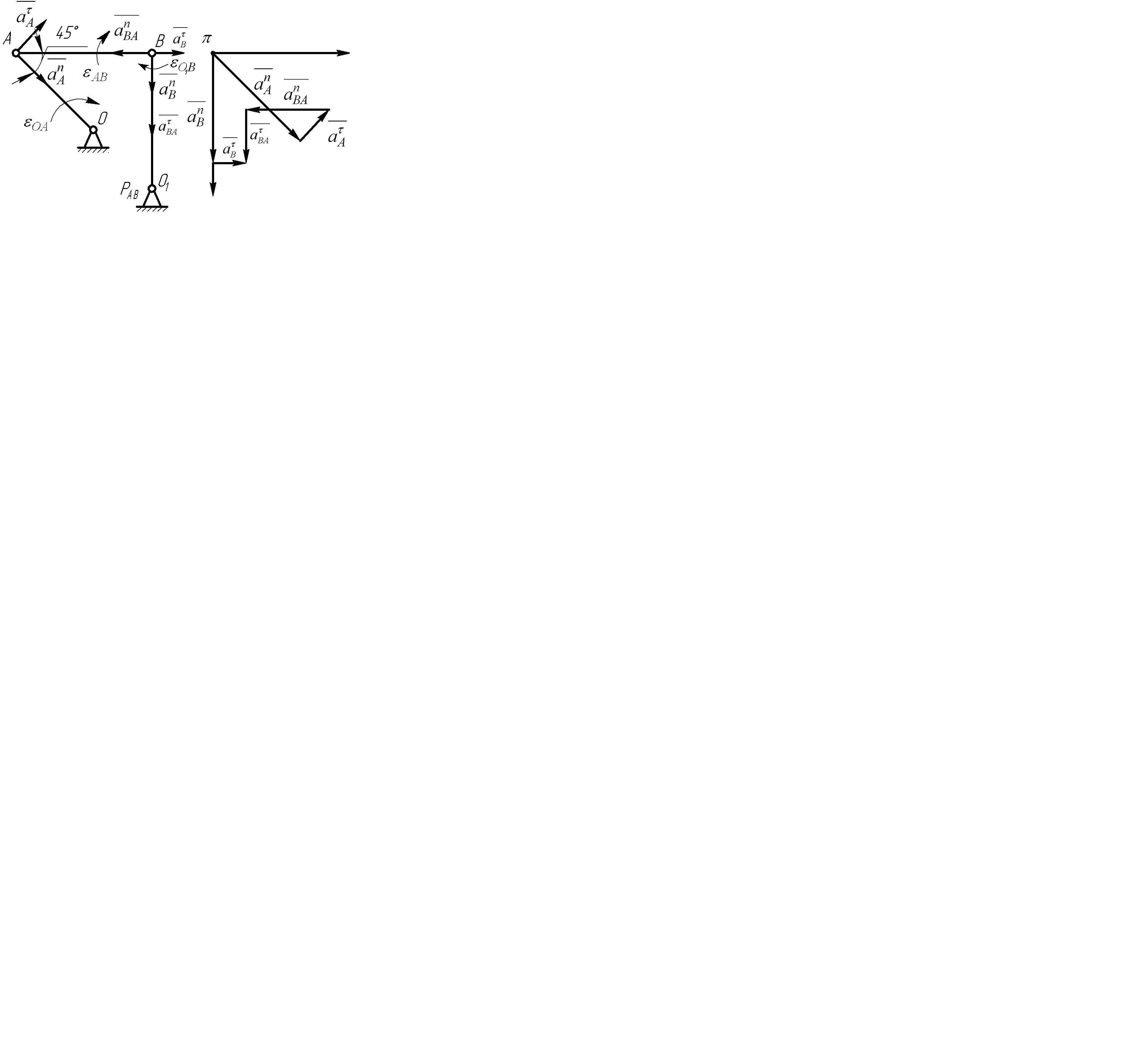
а) б)

Рис. 6.3.2(а) Схема механизма.(б) План ускорения

Складываем векторы ускорений, пользуясь правилом последовательного сложения векторов согласно равенству (6.3.1).

Проецируем на оси координат:

Х:

У:

,

= .

Определяем полное ускорение точки В

, .

ПРИМЕР 6.4

Для заданного плоского механизма (рис.6.4.1) определить скорость и ускорение точек А и В, а также угловую скорость звена АВ двумя способами.

Необходимые данные: ; ОА=2м.

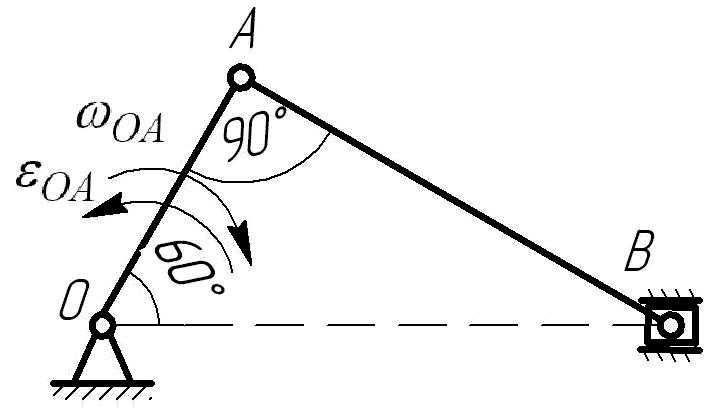
Рис.6.4.1

а) определим скорость точек механизма с помощью мгновенного центра скоростей.

По теореме об определение точек плоского механизма имеем:

Известно, что скорость точки при вращательном движении определяется следующим образом:

В нашем случае имеем: .

Построим положение мгновенного центра скоростей для звена АВ . Для этого покажем на схеме направления скоростей точек А и В. Вектор скорости направляется по касательной к траектории движения, т.е. перпендикулярна ОА. Вектор направляется вдоль неподвижной горизонтальной направляющей ползуна В. Восстановим перпендикуляры к и , на их пересечении получаем положение мгновенного центра скоростей (рис. 6.4.2). Определим расстояние от точек А и В до МЦС:

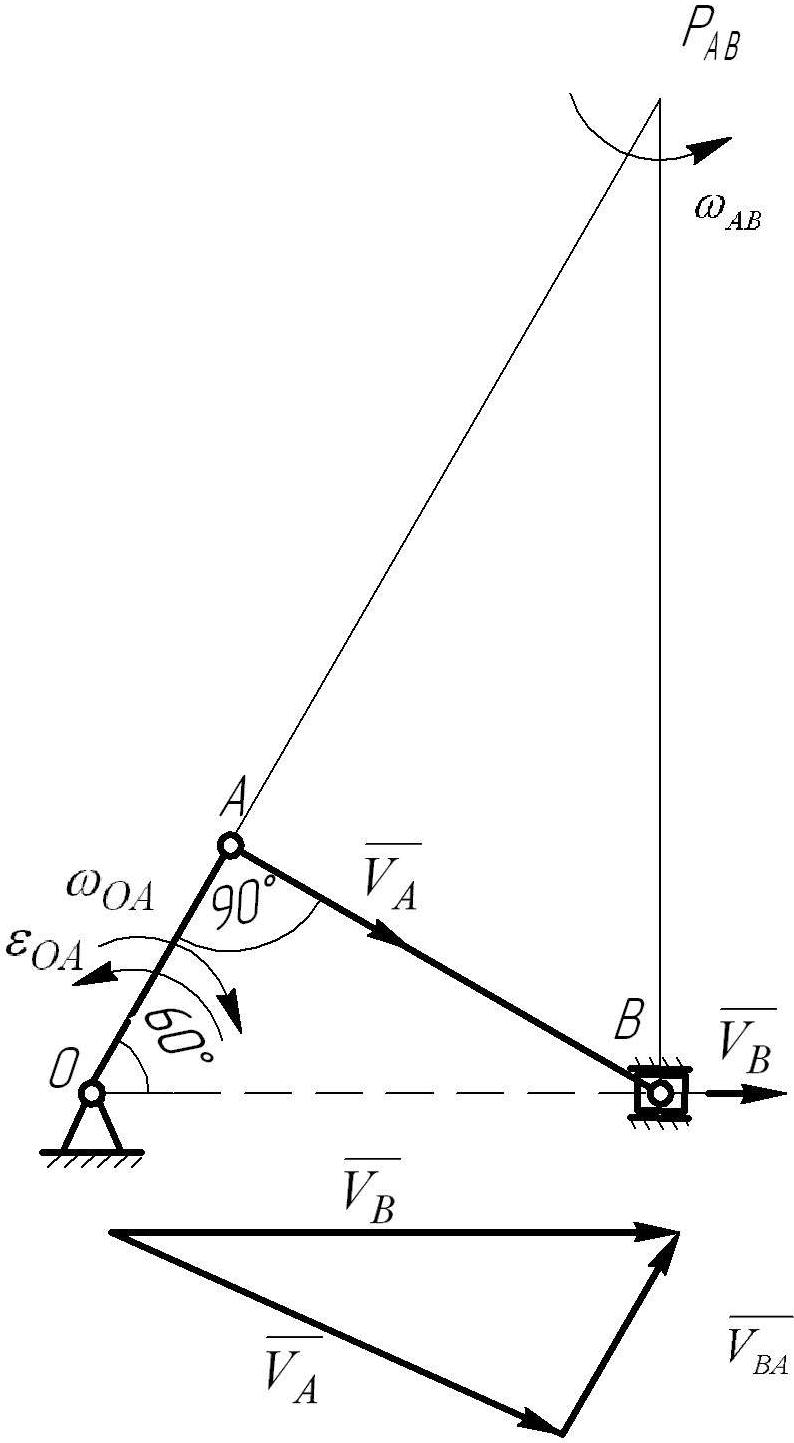
Рис.6.4.2 Схема механизма с построением МЦС звена АВ.

План скоростей.

Тогда величина искомой скорости точки В определяется предварительно просчитав угловую скорость звена АВ:

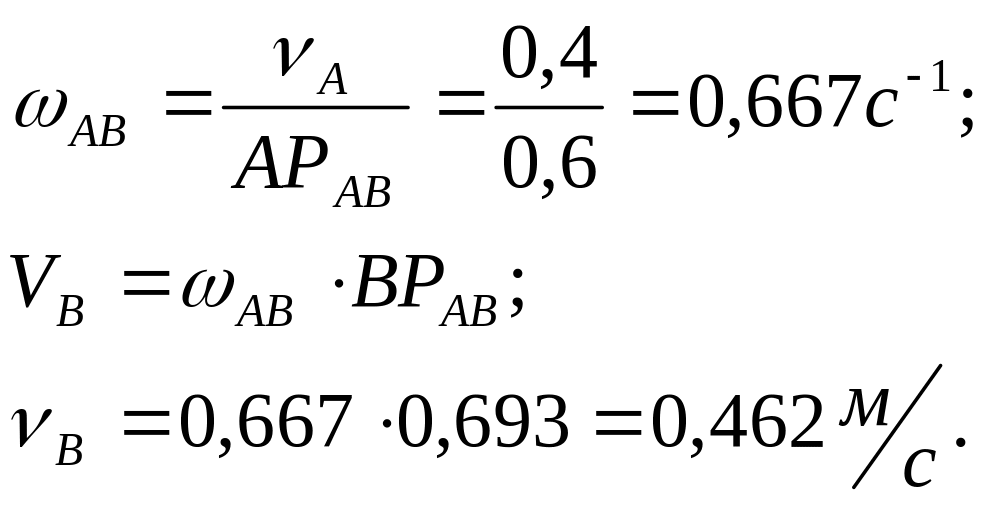
б) определим скорость точек механизма с помощью построения плана скоростей.

Известно, что скорость любой точки плоского механизма равна векторной сумме скорости точки, принятой за полюс ( ) и скорости точки вокруг полюса :

Анализируем векторную сумму в плане определения каждого вектора по величине и направлению. Так, вектор скорости точки А известен по величине и направлению:

( направлено перпендикулярно ОА в сторону ).

Линия действия направлена перпендикулярно АВ:

Вектор скорости точки В известен только по направлению вдоль неподвижных горизонтальных направляющих.

Строим план скоростей, пользуясь правилом сложения векторов (рис.6.4.2).

Из плана скоростей (рис. 6.4.2) имеем:

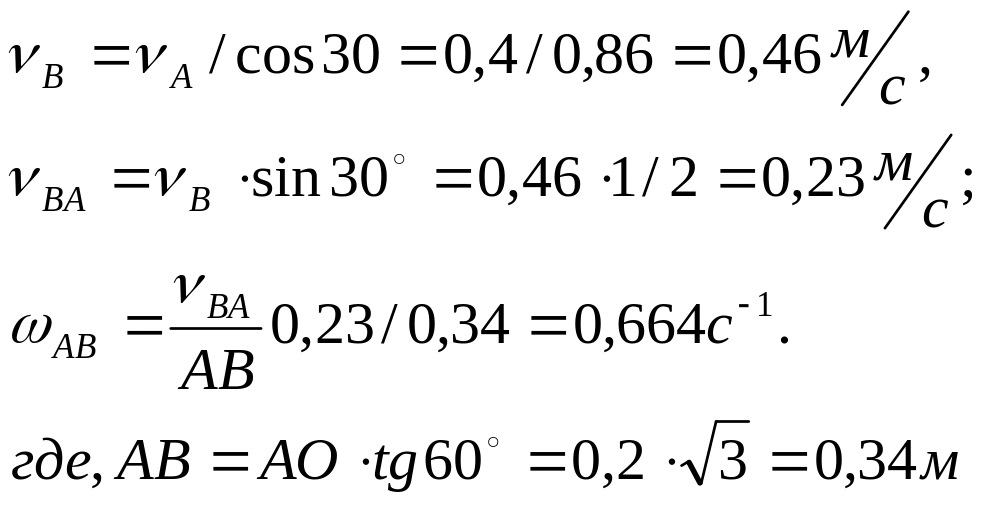
в) определим ускорение точек механизма графическим способом.

По теореме об определении ускорения точки при плоскопараллельном движении:

С учетом траекторий и вида движения выполним разложения по направлению на схеме механизма (рис. 6.4.3):

Определим каждое из ускорений по величине и покажем по направлению на схеме механизма:

вектор направляется от точки А по звену ОА к центру вращения точки О (рис. 6.4.3).

вектор направляется по касательной в сторону направления (рис.6.4.3):

.

Вектор направляется от точки В к А по звену АВ; перпендикулярно .

Строим план ускорений, пользуясь правилом сложения векторов (см. рис.6.4.3). Из плана ускорения получим

, .

г) определяем ускорения точек механизма аналитическим способом.

Проецируем векторную сумму ускорений на оси координат х, у (см. рис.6.4.3)

На ось Х:

На ось Y:

Подставим численные значения:

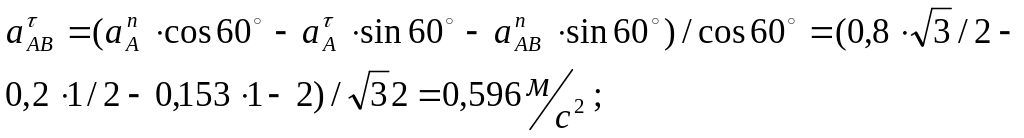
Угловое ускорение звена АВ:

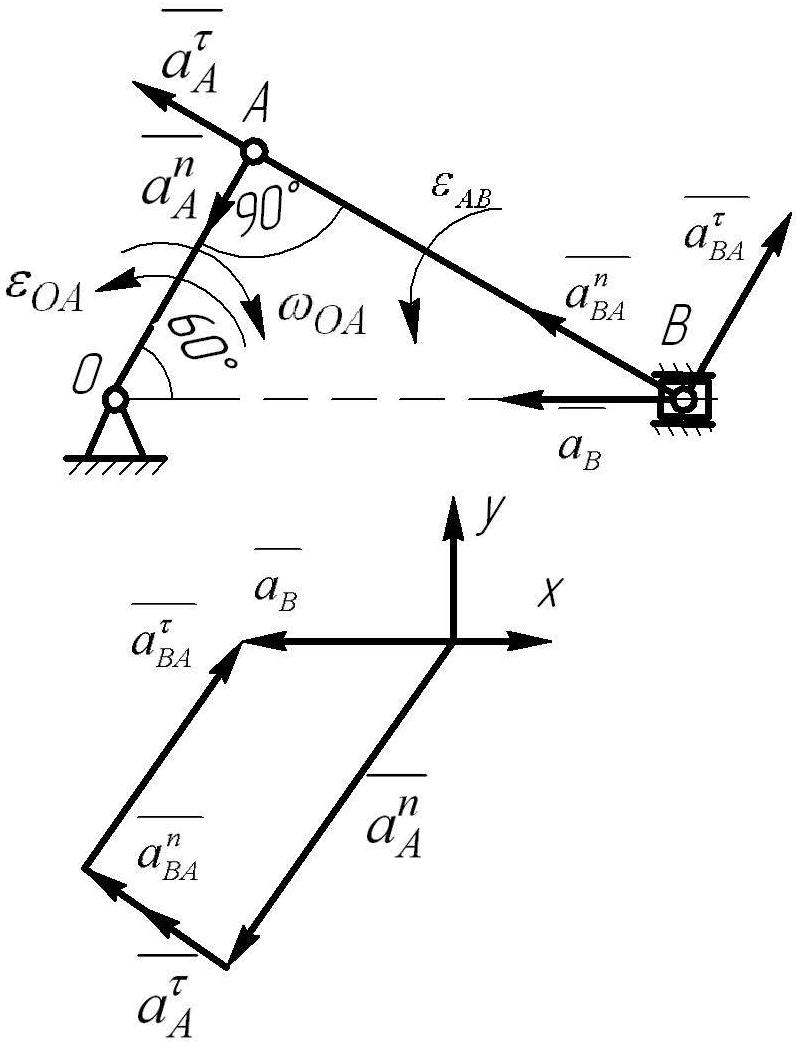
Рис. 6.4.3. Схема механизма. План ускорения.

ПРИМЕР 6.5

Кривошип О₁А вращается с постоянной угловой скоростью

Определить для данного положения механизма:

• скорости всех точек механизма и угловые скорости всех его звеньев с помощью мгновенных центров скоростей;

• скорости всех точек механизма и угловые скорости всех его звеньев с помощью плана скоростей;

• ускорения указанных точек механизма и необходимые угловые ускорения звеньев, с помощью плана ускорений;

• положение мгновенного центра ускорений указанного звена.