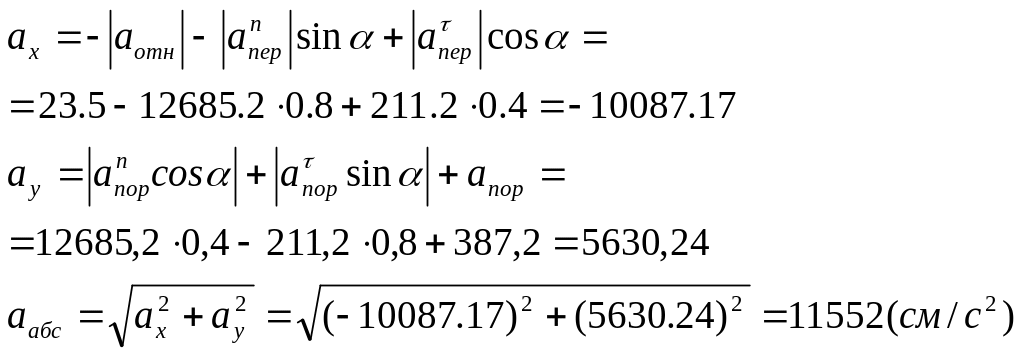3.4 Определение абсолютной скорости и абсолютного

ускорения точки в случае вращательного переносного движения

ПРИМЕР 5.2

Дано: S_отн =20cos(t/4), см; _пер=1,2t– t², рад; t₁=4/3с; R= 0см; а=20см.

Для схемы (рис 5.2.1) определить в момент времени t=t₁, абсолютную скорость и абсолютное ускорение точки М.

Решение:

Рассмотрим сложное движение точки М: относительное – это движение точки М по окружности радиуса R вокруг центра – точки О₁ (поступательное движение); переносное – это движение точки М вместе с телом Д вокруг неподвижной вертикальной оси (вращательное движение).

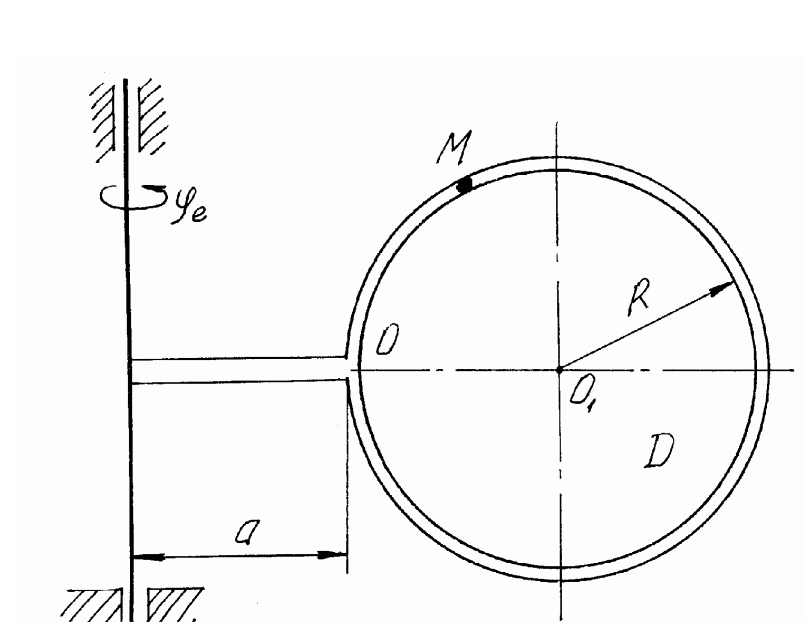
Рис. 5.2.1

Определяем абсолютную скорость точки М:

Относительная скорость:

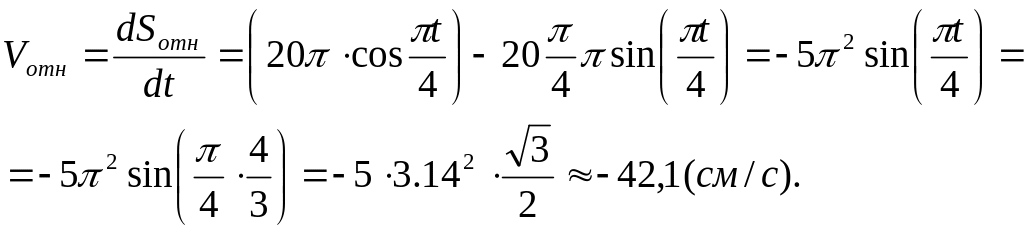
Знак “-“ показывает, что вектор V_отн направлен в сторону убывания S_отн.

Переносная скорость:

;

где r - расстояние от положения точки М до вертикальной оси вращения в данный момент времени t=t₁.

Это положение точки определяется центральным углом:

Этой дуге соответствует центральный угол :

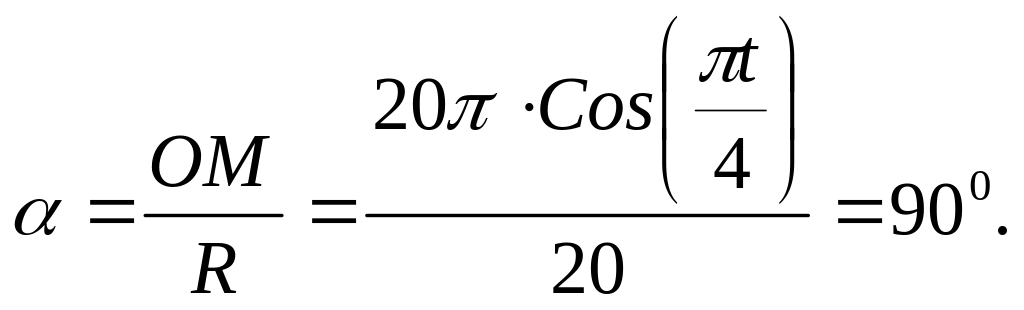
На схеме отмечаем истинное положение точки М, определяемое центральным углом .

Определяем угловую скорость:

Знак “-“ показывает, что вращение вокруг вертикальной оси происходит в сторону, обратную направлению отсчета угла . Поэтому вектор _пер направлен по оси вертикально вниз.

Итак:

Вектор V_пер направлен по касательной к окружности с центром в точке А на вертикальной неподвижной оси и радиусом r=a+R в сторону угловой скорости (рис.5.2.2).

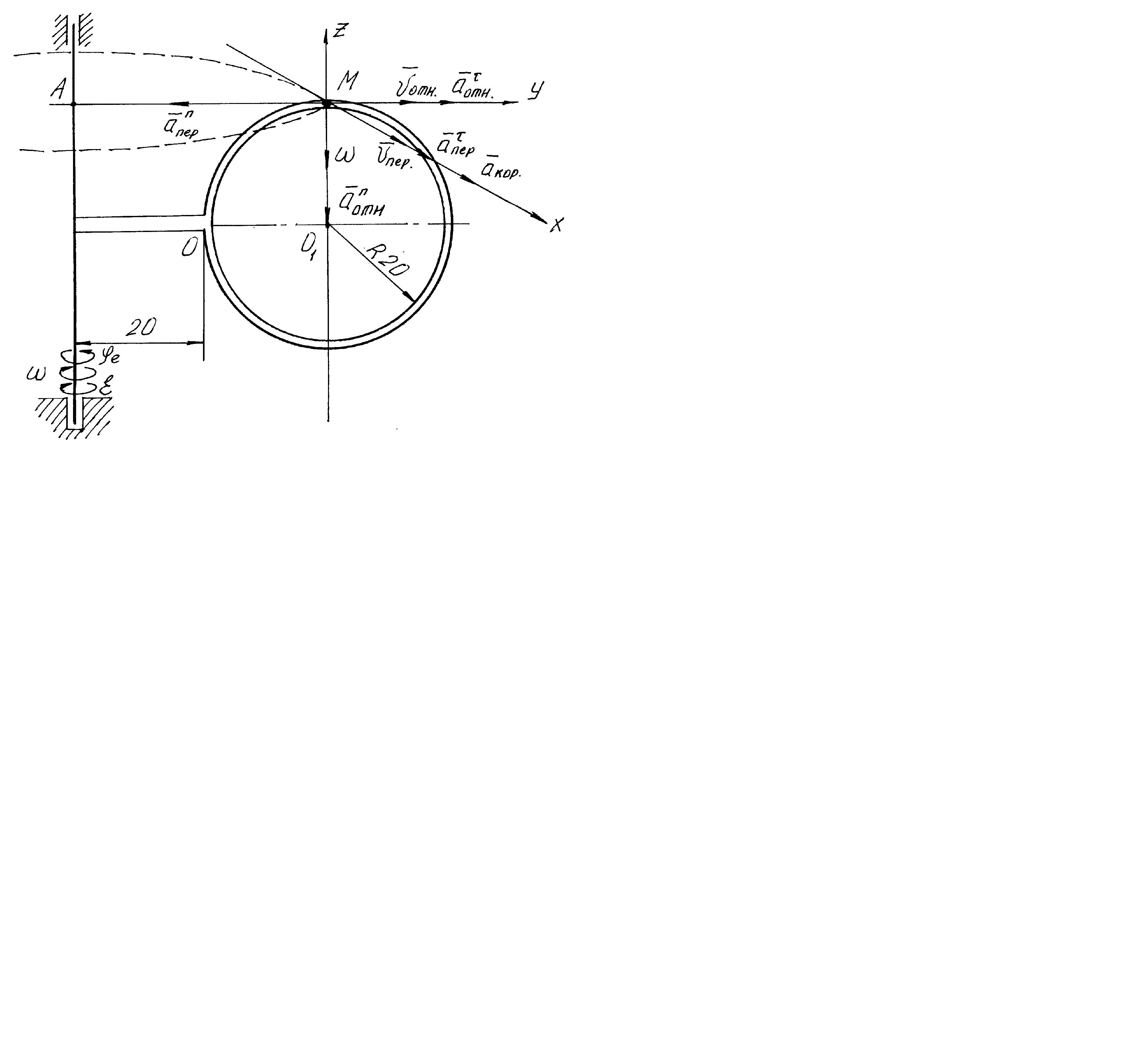
Рис. 5.2.2

Окончательно получаем:

.

Определяем абсолютное ускорение точки М:

.

Учитывая вид и траекторию движения имеем:

Определим каждую составляющую:

Вектор направлен от точки М по радиусу к центру «О₁»:

Вектор направлен по касательной к окружности радиуса R в сторону скорости , так как и имеют одинаковые знаки (рис.5.2.2):

Вектор направлен от точки М по радиусу к центру вращения А (рис.5.2.2.).

Угловое ускорение определяется по формуле:

.

Угловое ускорение направлено в сторону угловой скорости, так как и имеют одинаковые знаки:

.

Тогда:

.

Вектор направлен по касательной к траектории переменного движения в сторону углового ускорения.

Кориолисово ускорение:

Вектор угловой скорости направляется вдоль оси вращения вертикально вниз, поэтому имеем следующую скалярную форму:

.

Вектор a_кор направляется согласно правила определения направления кориолисова ускорения (рис.5.2.2.).

Спроецируем векторную сумму ускорений на оси координат:

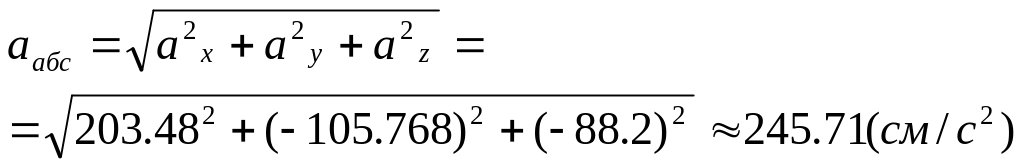
ПРИМЕР 5.3

Дано: ОМ=Sr=Sr(t)=25sin(t/3), см;

_с=_с(t)=25t²-0.5t, рад;

t₁=4c; а=25 см.

По заданным уравнениям относительно движения точки и движения тела D (рис.5.3.1) определить для момента времени t=t₁ абсолютную скорость и абсолютное ускорение точки М.

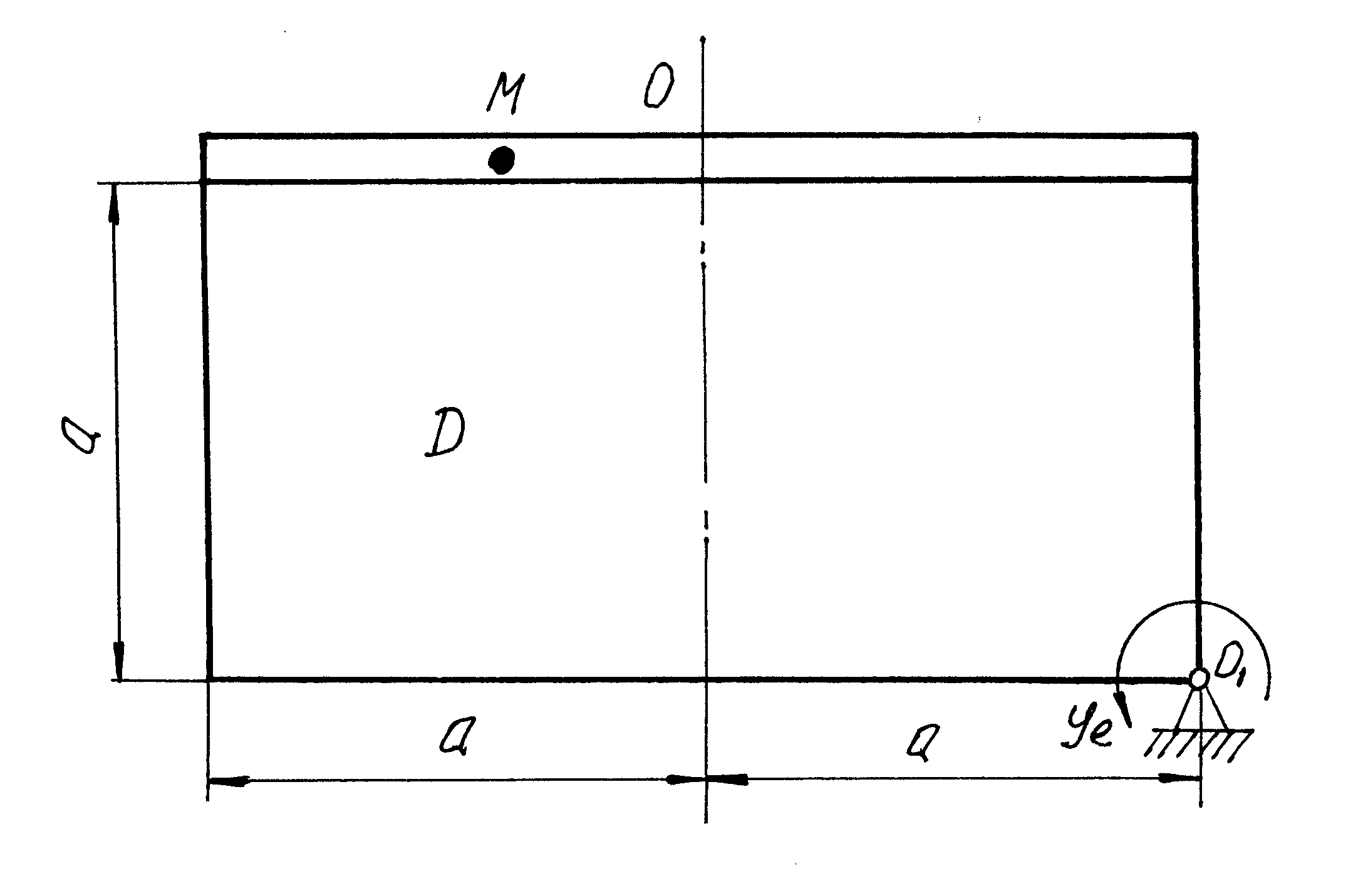
Рис.5.3.1

Решение:

Рассмотрим сложное движение точки М: относительное движение точки – движение точки М относительно подвижной системы координат тела Д (поступательное движение).

Переносное движение точки – движение точки М вместе с телом Д относительно неподвижной оси вращения (вращательное движение).

Определим абсолютную скорость точки:

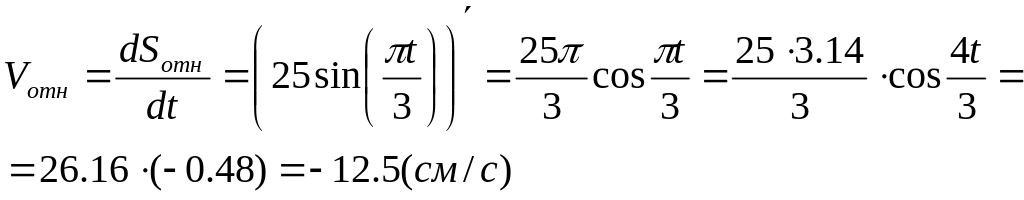
Отрицательный знак у показывает, что вектор направлен от точки М в сторону уменьшения расстояния S_отн (рис.5.3.2.)

.

Положительный знак у величины показывает, что и направлены в одну сторону (рис.5.3.2):

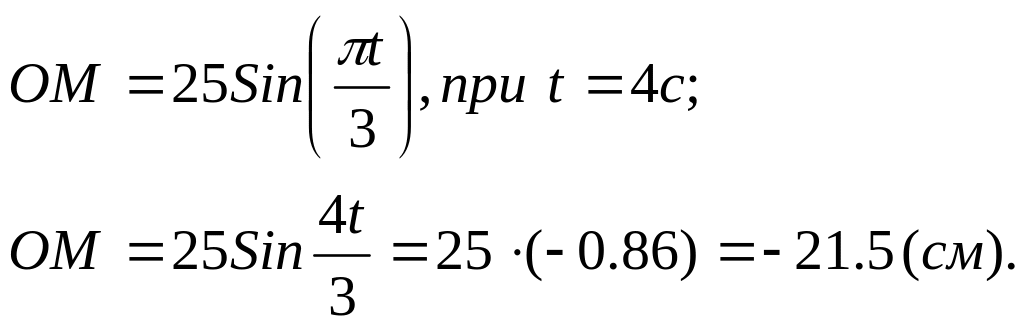
Треугольник прямоугольный, для которого имеем:

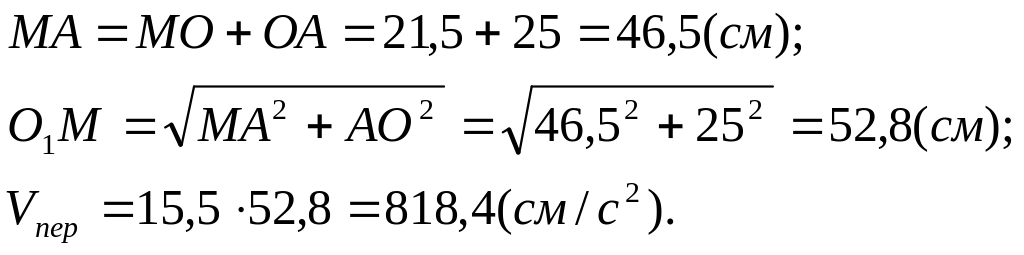
Вектор направлен по касательной к окружности О₁М в сторону вращения тела (рис.5.3.2).

;

; ;

Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений:

или в развернутом виде:

Положительный знак у показывает, что вектор направлен в противоположную сторону (рис.5.3.2).

Центростремительное ускорение в переносном движении определяется:

Вектор направлен от точки М к центру вращения О₁ (рис.5.3.2).

Касательное ускорение в переносном движении определяется следующим образом (рис.5.3.2):

Положительный знак углового ускорения показывает, что угловое ускорение направлено в сторону угловой скорости (рис.6.3.2.4).

Тогда получаем:

Вектор касательного ускорения направляется перпендикулярно О₁М в сторону углового ускорения (рис.5.3.2).

Королисово ускорение определяется:

Модуль Кориолисова ускорения:

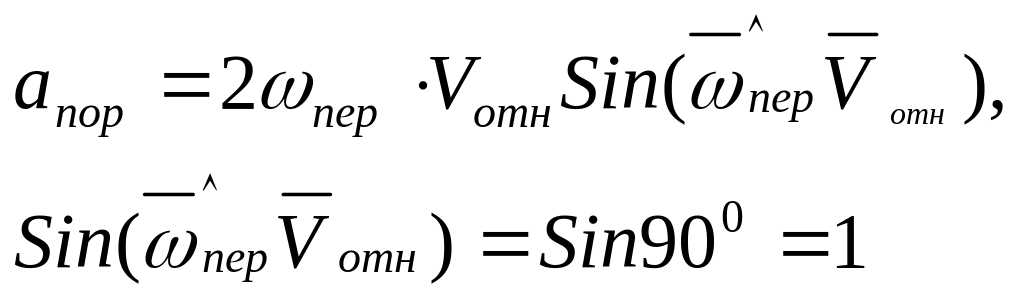
тогда

Вектор направляется согласно правила приведенному выше (рис.5.3.2).

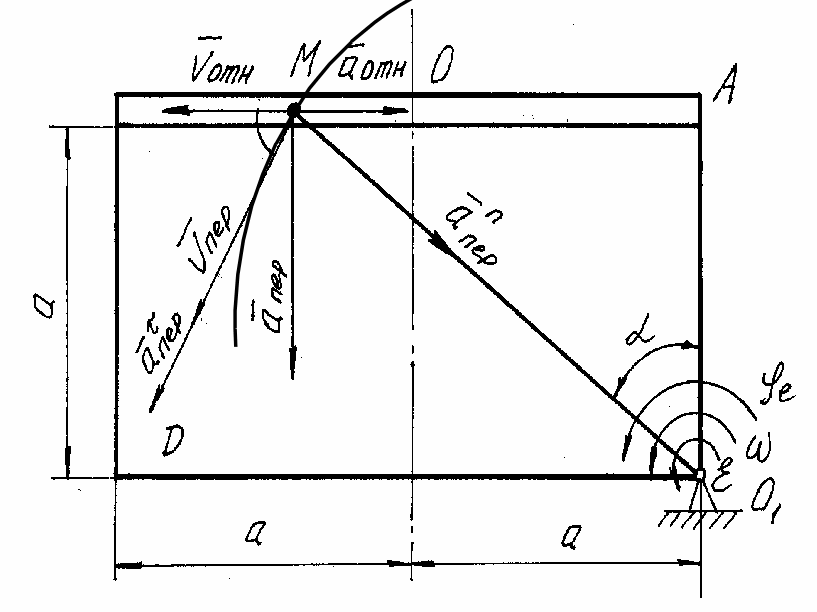
Рис. 5.3.2

Модуль абсолютного ускорения точки М находим способом проекций на оси координат: