Задача к-5.

3.3 Определение абсолютной скорости и абсолютного ускорения точки вслучае плоскопараллельного переносного движения

ПРИМЕР 5.1

Круглый диск радиуса R=100 см катиться без скольжения по прямолинейному горизонтальному пути (рис. 5.1.1) так, что его центр О движется с постоянным ускорением . В диске по дуге окружности радиуса R₁=40см. С центром в точке О_I проделан тонкий канал, по которому от А к B равномерно движется шарик М со скоростью 40 см/сек [4]. Найти абсолютную скорость и абсолютное ускорение шарика, когда он находиться на кротчайшем расстоянии от центра диска, если в этот момент отрезок ОО_I горизонтален, а скорость центра диска равна 50 см/сек.

Решение:

Шарик совершает сложное движение. Свяжем подвижную систему координат ОXY с диском, тогда переносным движением будет плоскопараллельное движение диска. В связи с отсутствием скольжения мгновенный центр скоростей диска находиться в точке Р касания колеса с плоскостью.

Мгновенную угловую скорость диска найдём по формуле

,

где - скорость центра диска в текущий момент,

OP - расстояние от точки О до М.Ц.С. Р

Дифференцируя по времени мгновенную угловую скорость диска, находим его мгновенное угловое ускорение:

.

В тот момент, когда скорость центра диска равна 50 см/сек, его мгновенная угловая скорость будет:

.

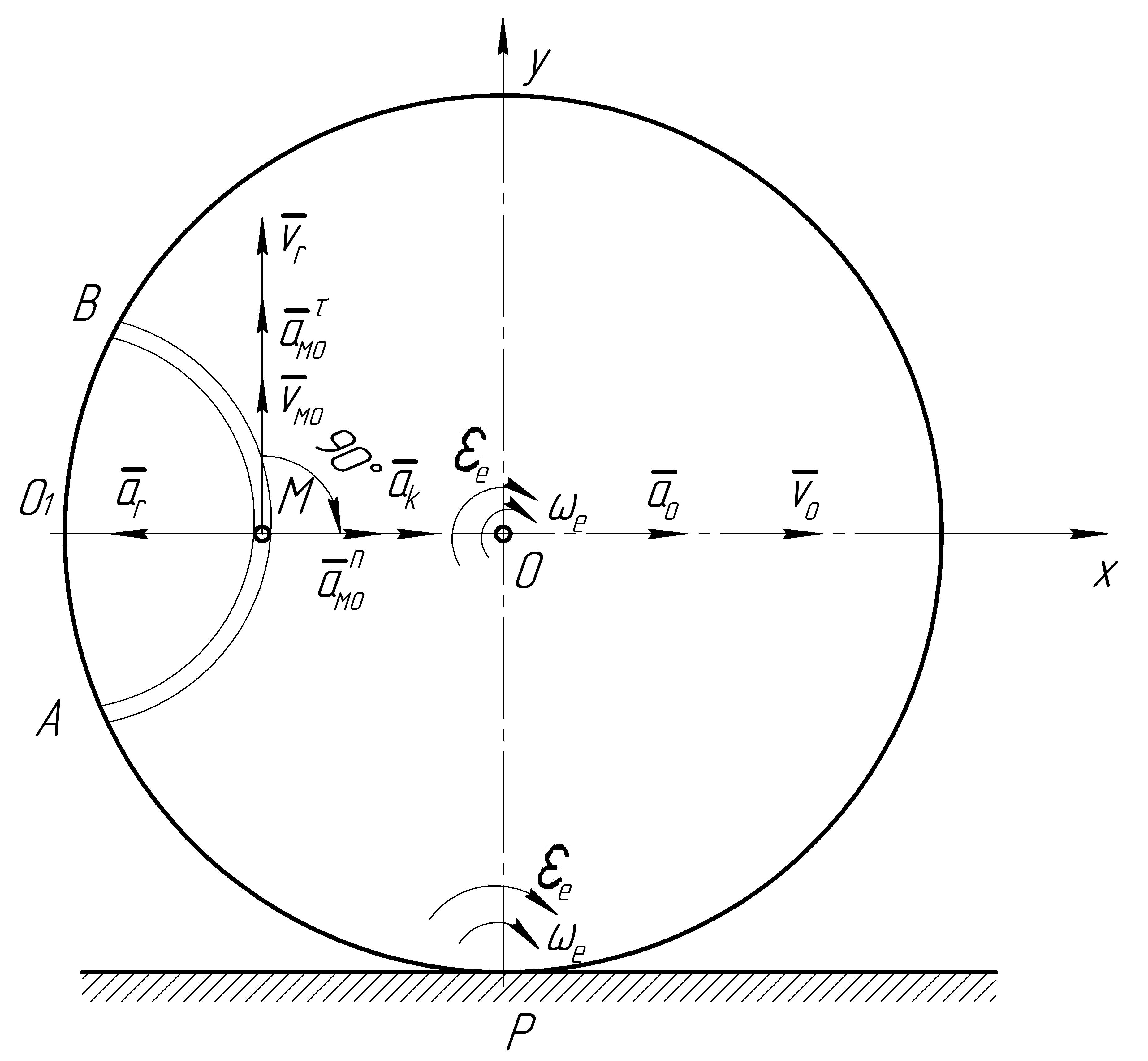
Рис.5.1

Направление вращения вектора вокруг точки Р показывает, что направление мгновенной угловой скорости совпадает с направлением вращения часовой стрелки. Вектор перпендикулярен плоскости диска и направлен от наблюдателя. Т.к. и имеют одинаковые знаки, направления совпадает с направлением _.

Переносная скорость и переносное ускорение шарика М равна соответственно скорости и ускорению той точки М диска, с которой в данный момент совпадает шарик.

Примем точку О за полюс, тогда переносная скорость шарика будет равна векторной сумме скорости полюса и скорости вращении точки М вместе с диском вокруг полюса т.е.:

_,

Покажем и дуговыми стрелками вокруг полюса О.

Модуль скорости полюса см/сек. Вектор направлен по оси х.

Найдём модуль скорости :

_.

Скорость направлена и перпендикулярно к ОМ в сторону переносного вращения вокруг полюса О.

Переносное ускорение шарика равно векторной сумме ускорения полюса и ускорения точки М в ее вращении вместе с диском вокруг полюса, т.е.:

Модуль ускорения полюса . Вектор направлен по оси Х.

Касательная составляющая направлена перпендикулярно МО.

Её направление соответствует направлению , показанному в полюсе О.

Нормальная составляющая направлена от М к О.

Величины , найдём по известным формулам:

,

.

Относительным движение шарика М будет его равномерное движение по окружности радиуса R₁=40см со скоростью относительное ускорение шарика равно векторной сумме касательного и нормального ускорений

т.к. =const, то величина касательного ускорения .

Модуль нормального ускорения:

.

Нормальное ускорение направленно от М к О_I. Т.о. относительное ускорение _..

Кориолисово ускорение шарика определим по формуле:

Т.к векторы _e и взаимно перпендикулярны, то модуль Кориолисова ускорения:

Направление _k найдём, повернув вектор относительной скорости на 90 в сторону переносного вращения. Т.о. в данный момент ускорение будет направленно от М к О.

Перейдём теперь к определению абсолютной скорости и абсолютного ускорения шарика. Согласно теореме о сложении скоростей:

, но ,

поэтому:

Все три вектора, стоящие в правой части этого равенства, известны как по величине, так и по направлению.

Найдём проекции вектора абсолютной скорости на оси координат.

,

.

Модуль абсолютной скорости:

.

Согласно теореме Кориолиса:

_, но и

поэтому .

Таким образом, все векторы, стоящие в прямой части этого равенства, известны и по величине и по направлению.

Найдём проекции вектора абсолютного ускорения на оси координат:

_,

_.

Модуль абсолютного ускорения:

.