Задача к-2. Составление уравнений движения точки и определение ее скорости и ускорения

ПРИМЕР 2.1

Для точки М заданного механизма составить уравнения движения, вычертить участок ее траектории и для момента времени .

Найти скорость точки, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в соответствующей точке.

Исходные данные: схема механизма (рис. 4.4.1.1); рад; r = 20 см; R = 100 см; t₁=1/3 с [2].

Решение:

Из условия P = P имеем:

; .

При t=1/3 с , .

Уравнения движения точки М (рис. 2.2):

;

и ли окончательно:

(2.1)

Эти уравнения являются параметрическими уравнениями траектории точки - эпициклоиды. Проекции скорости точки на оси координат:

см/с;

см/с.

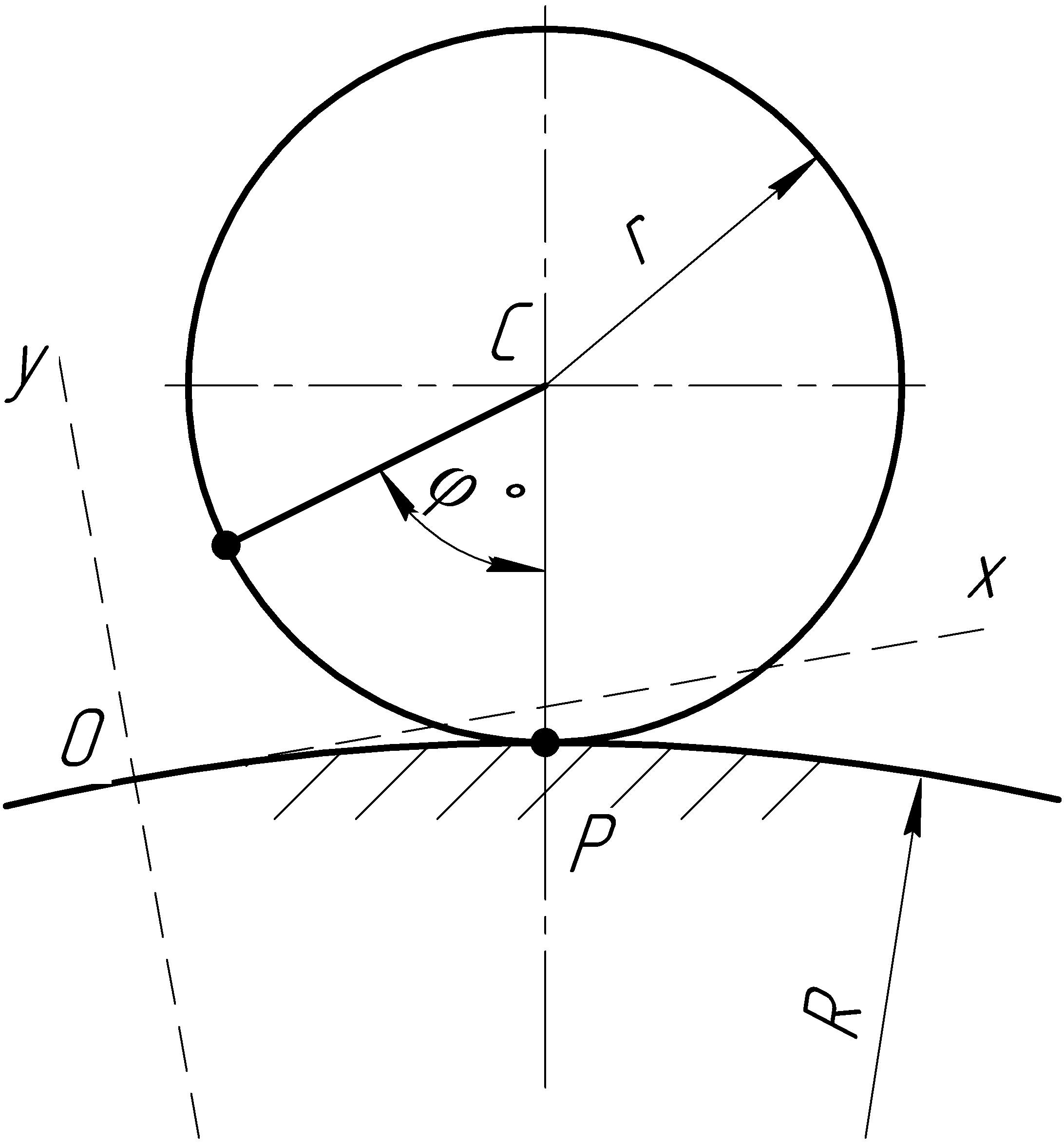
Рис. 2.1

Модуль скорости:

или окончательно

см/с . (2.2)

Проекция ускорения точки на оси координат

;

.

Модуль ускорения

или

см/с².

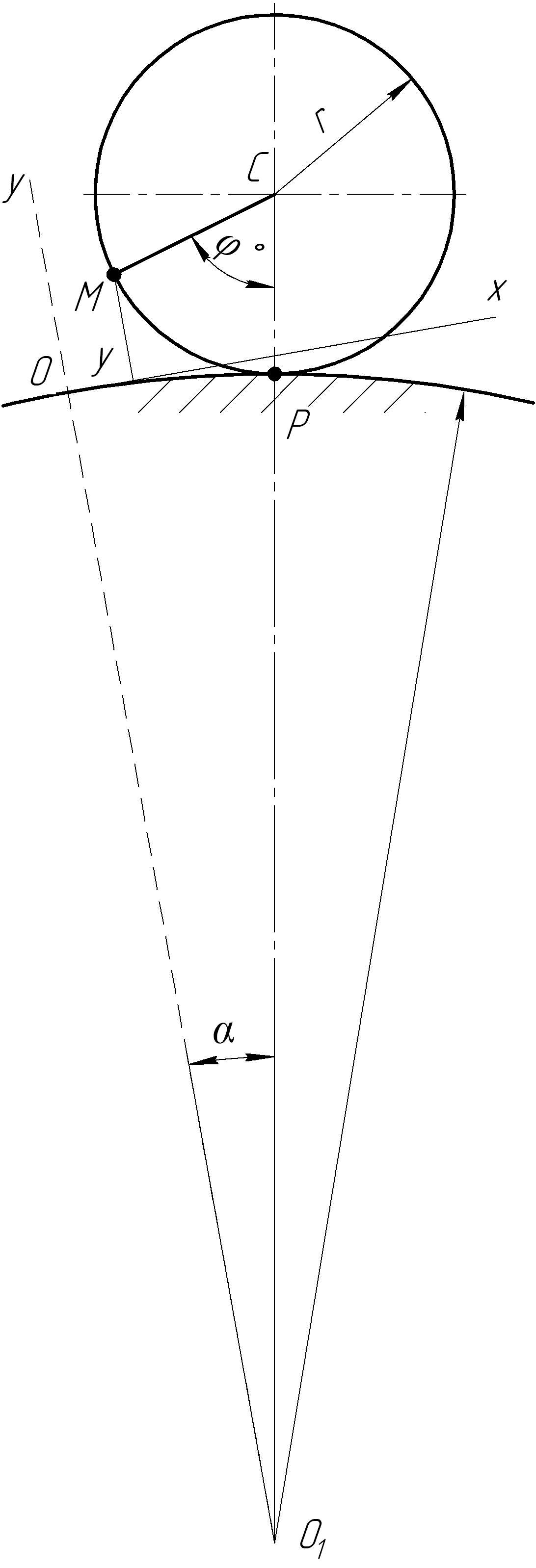
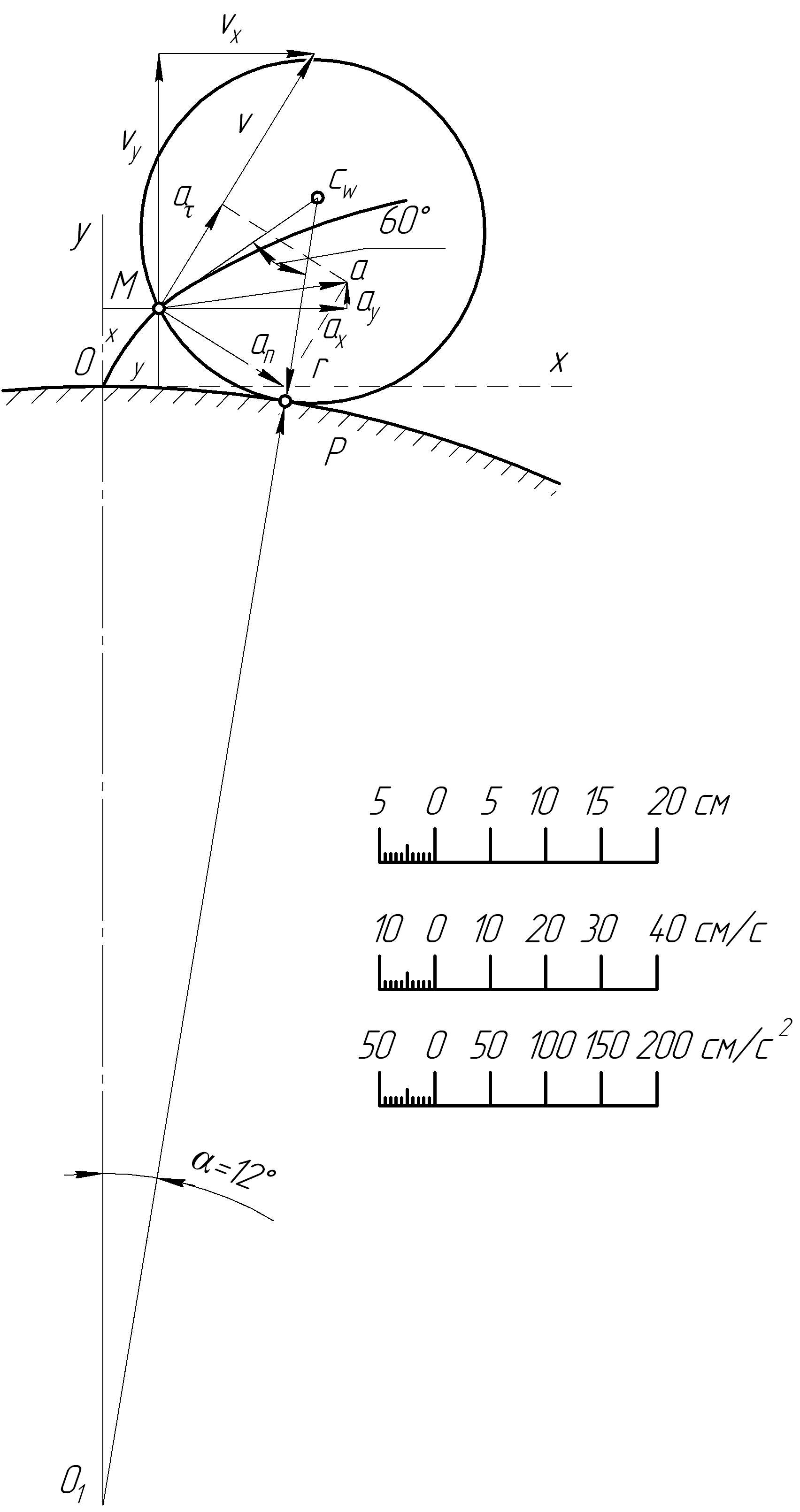
Рис.2.2. Рис.2.3.

Так как в данном примере для модуля скорости точки получено простое выражение, то модуль касательного ускорения находим не по формуле

см/с²,

а непосредственным дифференцированием выражения (2.2):

или

см/с².

Модули скорости и ускорения точки, их проекции на оси координат, а также касательное и нормальное ускорения, вычисленные для заданного момента времени t=1/3 с, приведены в таблице 2.1.

Таблица 2.1

Скорость м/с			Ускорение м/с2					Радиус кривизны см
30,4	56,0	75,4	260	41	263	204	166	34,3

Нормальное ускорение точки:

см/c².

Радиус кривизны:

см.

Значения и также приведены в таблице 2.1.

На рис.2.3 показан участок траектории точки М, построенный по уравнениям (2.1), а также ее скорость, ускорение и все их составляющие. Таким образом, как и при выполнении задания К-1, осуществляется графическая проверка правильности вычислений.

ПРИМЕР 2.2

Определить вид траектории движения точки, найти ее положение при , а также определить ее скорость, нормальное, тангенциальное, и полное ускорение точки, если

Решение:

Определим вид траектории в координатной форме, исключив переменную из уравнений координат, найдем зависимость:

Траекторией движения точки является парабола, ветви которой вытянуты вдоль оси ОХ, вершина в О (-3,0) (рис.2.2.1).

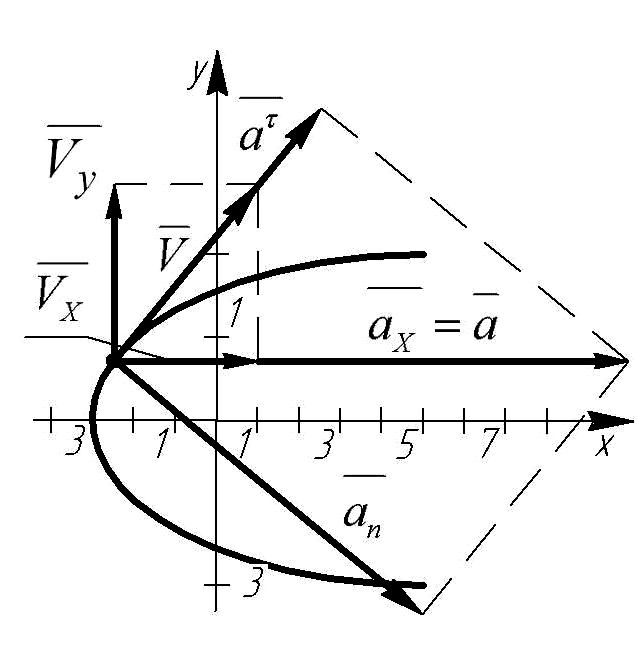
Рис.2.2.1

Определяем координаты точки М при , для этого в уравнение движения подставляем :

покажем точку М на траектории.

Определяем скорость точки:

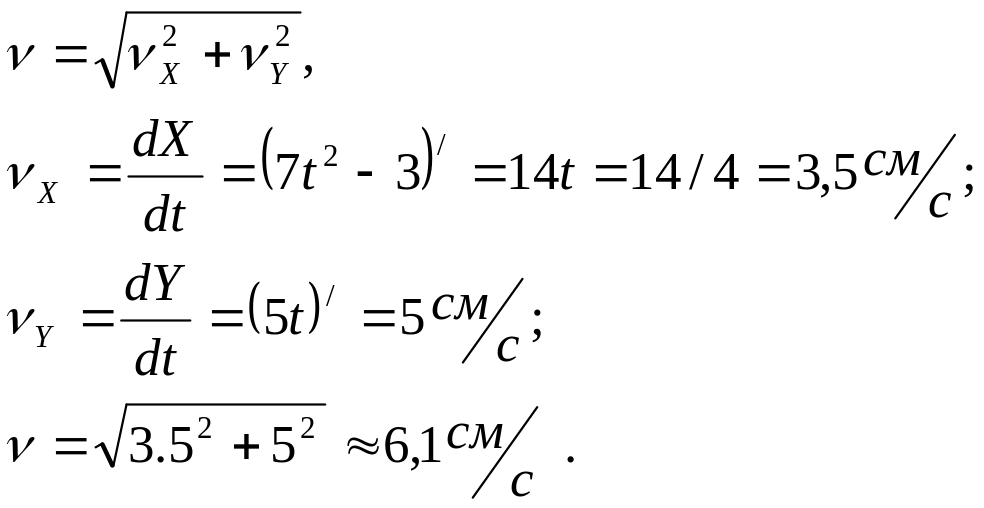
Определяем полное ускорение точки.

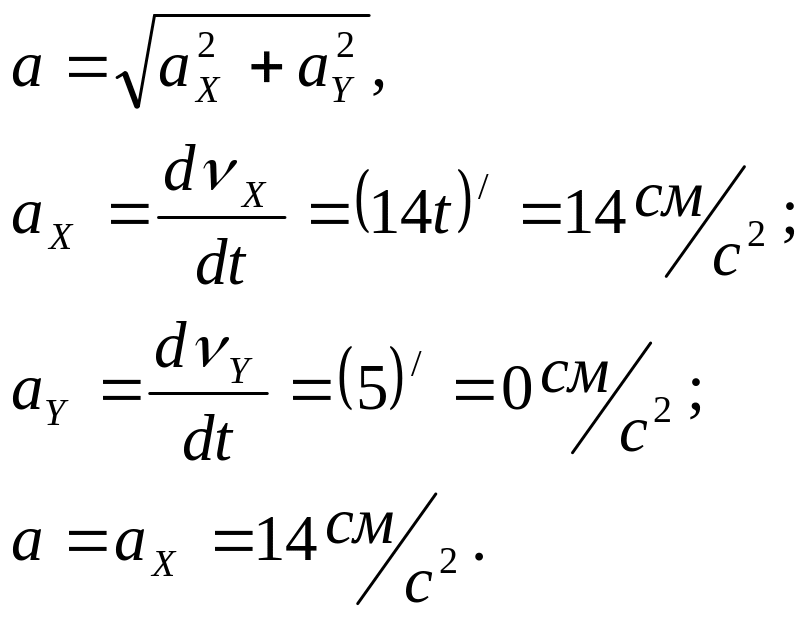
Определяем тангенциальное, нормальное ускорение точки, а также радиус кривизны окружности:

Нормальное ускорение:

Радиус кривизны траектории:

Покажем на рисунке 4.4.4 скорости , , , , и точки М.

II КИНЕМАТИКА ТВЕРДОГО ТЕЛА

ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ

ТВЕРДОГО ТЕЛА.

Задача К-3.

Определение скоростей и ускорений точектвердого тела при поступательном и вращательном движении.

ПРИМЕР 3.1

Ведущий шкив I изображенного на чертеже механизма лебедки (рис. 5.1.1.1) начинает вращаться равноускоренно из состояния покоя и за первые 5 секунд совершает 50 оборотов. Определить скорость и ускорение груза D а также точки В, расположенной на поверхности барабана через I секунду после начала движения. Радиусы шкивов 1 и 2 и барабана соответственно равны: см, см, см [4].

Число зубьев колес 3 и 4 равны , . Шкив 2 неизменно соединён с колесом 3, а колесо 4 - с барабаном 5.

Решение:

Ведущий шкив 1 совершает равнопеременное вращение, уравнение которого имеет вид: .

где: - угол поворота шкива 1 в радианах.

- начальный угол поворота шкива 1

- начальная угловая скорость шкива 1

- угловое ускорение шкива 1

По условию , .

Угол поворота шкива 1 задан в полных оборотах и равен N₁=50 оборотов. В радианах .

После подстановки значений уравнение вращения шкива 1 примет вид: . Отсюда находим угловое ускорение шкива сек^-2.

Угловая скорость шкива 1 определяется уравнением .

Отсюда, учитывая, что и сек^-2 получаем .

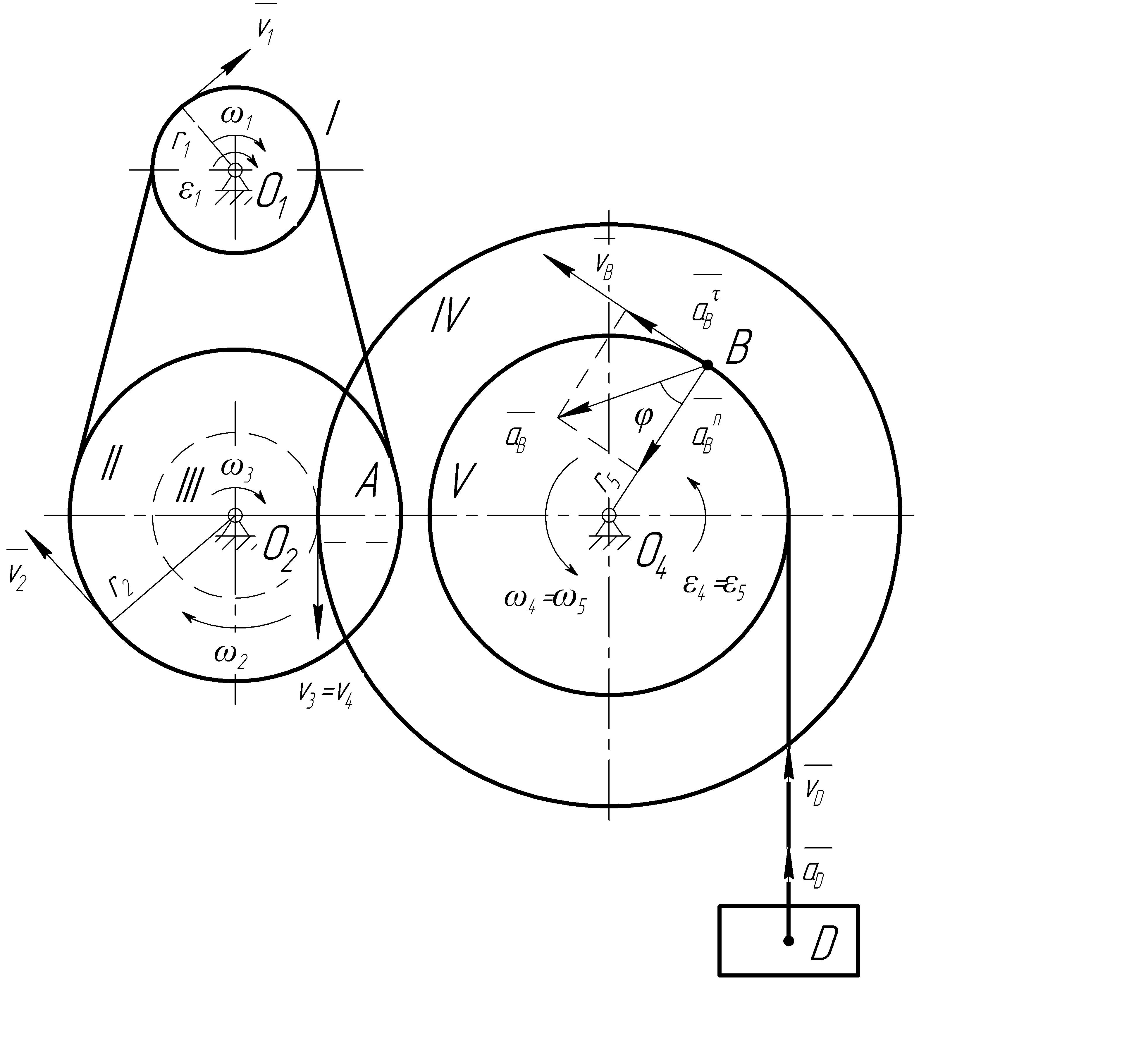
Рис.3.1.1

Для определения угловой скорости шкива 2 воспользуемся равенством окружных скоростей на ободах первого и второго шкивов, т.е. , с другой стороны и , поэтому . Отсюда .

Так как колесо 3 неизменно связанно со шкивом 2, то его угловая скорость равна угловой скорости шкива 2, т.е. .

Обозначим радиусы начальных окружностей зубчатых колёс 3 и 4 соответственно буквами и .

Для определения угловой скорости колеса 4 воспользуемся тем, что начальные окружности колёс 3 и 4 находящиеся в зацеплении, катятся друг по другу без скольжения и следовательно в точке зацепления линейная скорость точки А, принадлежащей колесу 3, равна линейной скорости точки А, принадлежащей колесу 4.

Следовательно . Отсюда, с учётом равенств , получаем:

, .

Радиусы начальных окружностей пропорциональны числам зубьев, поэтому и сек^-1.

Угловое ускорение колеса 4 найдём как производную по времени от его угловой скорости:

сек^-2.

Т.к. барабан 5 неизменно связан с колесом 4, то его угловая скорость и угловое ускорение равны соответственно угловой скорости и угловому ускорению колеса 4.

сек^-1, сек^-1.

В момент t₁=1 сек, угловая скорость и угловое ускорение барабана 5 будут:

, .

Скорость и полное ускорение точки B, расположенной на поверхности барабана в момент t₁=1сек, найдём по формулам:

, ,

, .

Направление полного ускорения определяем углом между ускорением и радиусом вращения точки В:

.

В связи с отсутствием проскальзывания каната по поверхности барабана скорость и ускорение груза D будут соответственно равны скорости и касательному ускорению точки B, т.е:

см/сек², .

ПРИМЕР 3.2

Механизм состоит из ступенчатых колес 1-3, находящихся в зацеплении или связаны ременной передачей, груз 4 и 5 и стрелки 6, жестко связанной с колесом 3. радиусы колес равно соответственно: 1- r₁=2 см, R₁=4 см, у колеса 2- r₂=6 см, R₂=8 см, у колеса 3- r₃=12 см, R₃=16 см, длина стрелки l=24 см (рис. 3.2.1). Закон изменения скорости груза 5 : υ₅=2(t­²-3) см/с², положительное направление которой вниз.

Найти скорости точек А и С, угловое ускорение колеса 3 и ускорение точек B и D и груза 4 в момент t₁=2 с.

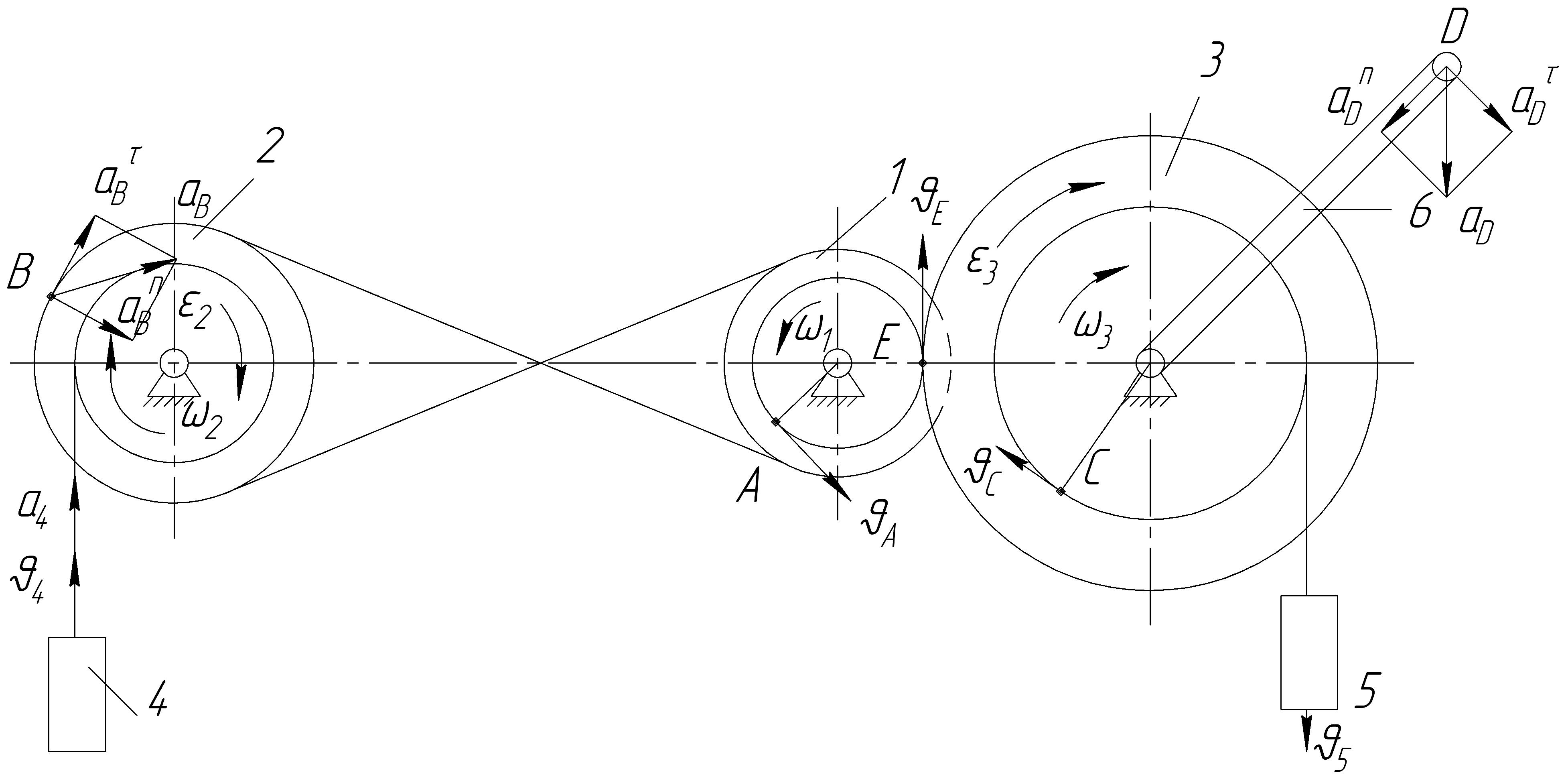
Рис.3.2.1

Решение:

Определим угловые скорости колес, как функции времени t. Зная υ₅, находим угловую скорость 3-го колеса

Так как колесо 3 и 1 находятся в зацеплении, то скорость точки Е зацепления этих колес одинакова, поэтому , откуда

Колесо 1 находится в зацеплении с колесом 2, поэтому , откуда

Направления угловых скоростей всех тел показаны на рис. 3.2.1

Определение углового ускорения 3-го тела ε₃. По известной угловой скорости ω₃; и при t₁=2 c. ε₃ =0,67с^-2.

Определение скорости точки А. по известной угловой скорости 1-го колеса:

, при t₁=2 c. см/с.

Определение скорости точки С. Так как точка С принадлежит колесу 3, то при t₁=2 c; см/с.

Направление скоростей точек А и С показаны на рисунке в соответствии с направлениями угловых скоростей.

Определение ускорения точки В. Предварительно находим угловое ускорение 2-го тела , при t₁=2 c. ε₂=2,67с^-2.

Ускорение точки В, причем при t₁=2 c.

см/с², см/с² см/с².

Направление показаны на рисунке 3.2.1

Определение ускорения точки D. При t₁=2 c ε₃ =0,67с^-2 , ω₃=0,17с^-1.

Находим при t₁=2 c

,

см/с²,

см/с², см/с².

Направление показаны на рисунке 3.2.1

Определение ускорения тела 4. сначала находим скорость этого тела

Так как груз 4 движется поступательно, то центр этого груза движется прямолинейно, а поэтому ,при t₁=2, ,

т.к. .

Замечание. Ускорение тела 4 можно найти как касательное ускорение точки обода колеса радиусом r₂ т.е. см/с².