1. Кинематика точки. Поступательное движение. Скорость и ускорение точки

1.1. Определение траектории движения точки

Чтобы получить уравнение траектории движения точки, необходимо найти зависимость между координатами, исключив переменную t из уравнений координат, то есть x=f(y).

а) уравнения движения точки имеют вид:

Выразим из второго уравнения переменную t: t=-y/3 и подставим первое уравнение:

Получаем уравнение параболы.

б) необходимо воспользоваться соотношениями между тригоно-метрическими функциями, в случае x=12cos(πt/6), y=4sin(πt/6).

Возведем в квадрат обе части каждого из уравнений и сложим правые и левые части уравнений:

Получим уравнение эллипса.

в) подбор коэффициентов и математические преобразования:

Умножим первое уравнение на 3, второе на 5, получим:

Вычтем из первого уравнения второе: 3x-5y=11.

Получим уравнение прямой линии: 3x-5y=11.

1.2 Определение скорости и ускорения точки

Скорость точки при поступательном движении определяется:

Вектор скорости направляется по касательной к траектории движения точки.

Ускорение точки определяется:

Нормальное ускорение точки:

где ρ – радиус кривизны траектории движения точки.

Нормальное (центростремительное) ускорение направляется от точки по радиусу кривизны к центру.

Тангенциальное ускорение определяется:

тангенциальное (касательно) ускорение направляется по касательной к траектории движения точки.

Полное ускорение точки равно:

направляется как результирующий вектор, построенный на нормальном и тангенциальном ускорениях точки (рис.1) [1].

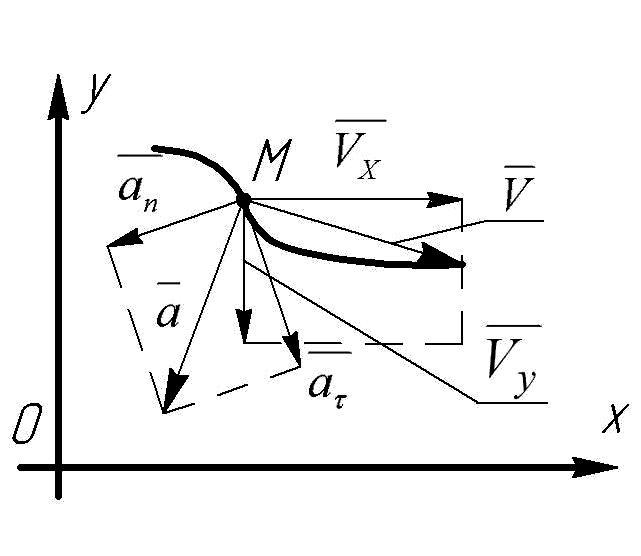
Рис.1.

В случае поступательного прямолинейного движения точки:

где ρ – радиус кривизны прямой (ρ= ).

Тогда

Задача к-1. Определение скорости и ускорения точки по заданным уравнениям ее движения

ПРИМЕР 1.1

Движение точки задано уравнениями: , (х, у-в см., t-в сек.) [4].

Требуется найти:

а) уравнение траектории движения точки, а также скорость и ускорение;

б) построить в осях координат график траектории движения точки;

в)нанести векторы скорости и ускорения для t=0;

г) определить тангенциальное, нормальное ускорение точки и радиус кривизны ее траектории, подсчитать эти величины для t=0.

Решение:

Чтобы найти уравнение траектории, надо исключить параметр t из уравнений движения.

Уравнения движения представим в виде:

; .

Т.к. , то можно записать:

или .

Это уравнение параболы. Теперь надо определить, вся ли парабола будет траекторией. Для этого проанализируем уравнения движения:

, т.к , то ,

, т.к , то .

Следовательно, можно заключить, что траекторией будет та часть параболы, для которой: , . Изобразим траекторию сплошной линией, а остальную часть параболы – пунктирной (рис 1.1).

Для определения скорости точки, найдем проекции вектора скорости на координатные оси:

, . (1.1)

Модуль скорости равен

(1.2)

Найдем также направляющие косинусы вектора скорости:

;

;

Определяем величину и направление вектора скорости при t=0, строим этот вектор на чертеже:

t=0, V=3π , , , , .

Для определения ускорения найдем проекции ускорения на координатные оси:

. (1.3)

Модуль ускорения:

. (1.4)

Направляющие косинусы вектора ускорения:

;

;

t=0, а=2π² , , , , .

Вектор ускорения для нулевого момента времени показываем на чертеже.

Определяем проекцию скорости на касательную. Положительное направление отсчета дуг на траекторию выберем вправо. На рис. 1.1 это направление указано вектором τ.

Как видно из формулы для V_Х при движении вправо , при движении влево . Поэтому, если в формуле (1.2) для модуля скорости отбросить знак модуля, то получим выражение для V_τ:

(1.5)

Зная зависимость V_τ от t, найдем касательное ускорение а_τ

(1.6)

При t=0 , а_τ=0.

Для нахождения а_п надо использовать зависимость:

, откуда:

.

При t=0, .

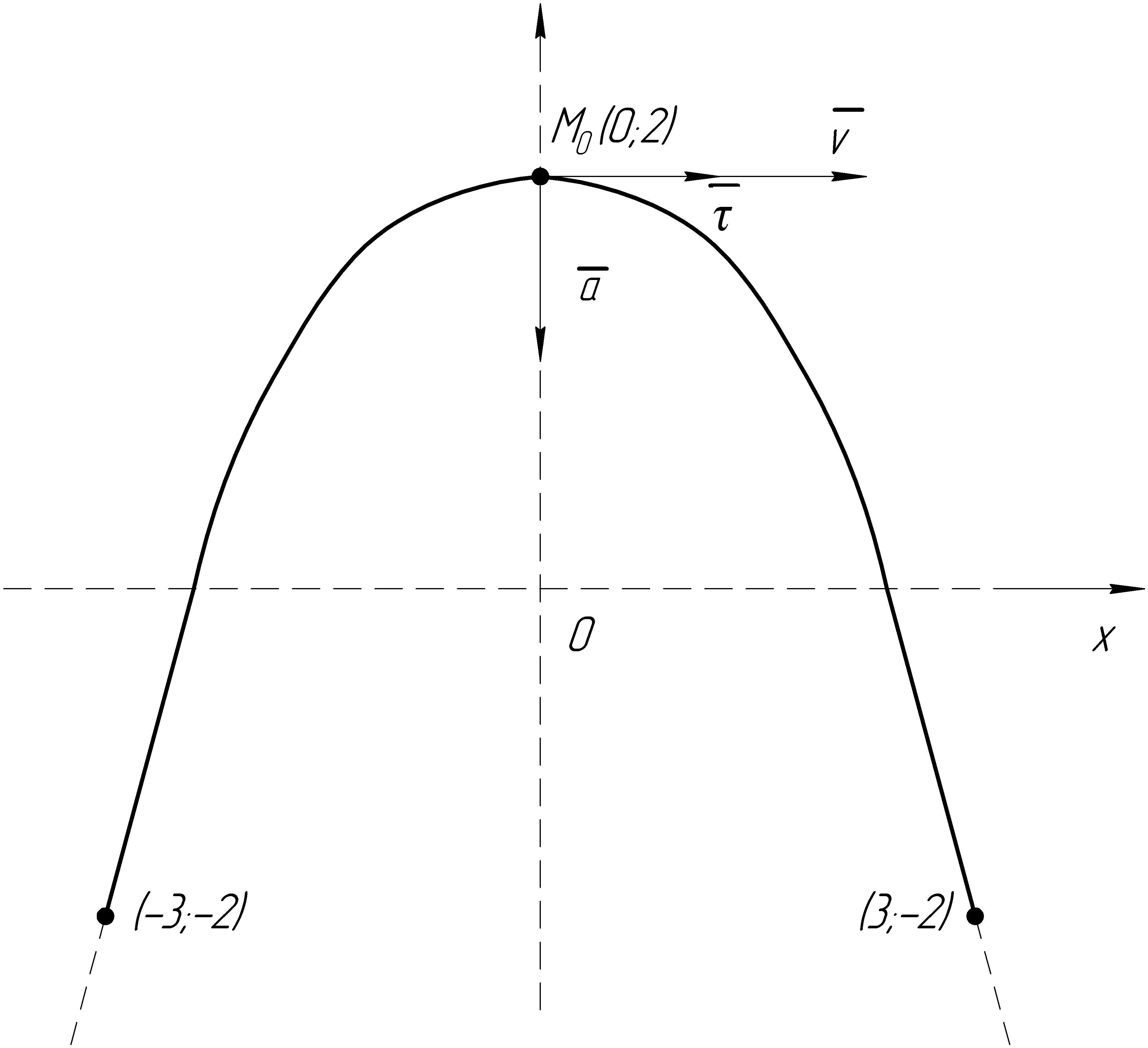
Рис. 1.1

ПРИМЕР 1.2

Определить траекторию, скорость и ускорение середины М шатуна кривошипно-ползунного механизма (рис. 1.2), если ОА=АВ=2b, а угол при вращении кривошипа растет пропорционально времени: [1].

Рис. 1.2

Решение:

Начинаем с определения уравнения движения точки М. Проводя оси и обозначая координаты точки М в произвольном положении через х и у находим:

, .

Заменяя его значением, получаем уравнения движения точки M:

, .

Для определения траектории точки М представим уравнения движения в виде:

.

Возводя эти равенства почленно в квадрат и складывая, получим:

.

Итак, траектория точки М — эллипс с полуосями 3b и b.

Теперь по формулам находим скорость точки M:

Скорость оказывается величиной переменной, меняющейся с течением времени в пределах от до .

Далее по формулам определяем проекции ускорения точки M:

, ;

отсюда:

,

где r - длина радиуса-вектора, проведенного из центра О до точки М. Следовательно, модуль ускорения точки меняется пропорционально ее расстоянию от центра эллипса.

Для определения направления имеем по формулам:

, .

Отсюда находим, что ускорение точки М все время направлено вдоль МО к центру эллипса.

ПРИМЕР 1.3

Определить вид траектории движения точки, найти ее положение при , а также определить ее скорость, нормальное, тангенциальное, и полное ускорение, если

, .

Решение:

Определим вид траектории движения точки: исключив переменную из уравнений координат, найдем зависимость:

.

Получаем уравнение эллипса:

Центр эллипса находится в точке с координатами (0; -3), полуоси эллипса равны 4 и 2.

Определяем координаты точки М при :

Точка М имеет координаты (-2; -4,7)

Определяем скорость точки:

Определяем полное ускорение точки.

Определяем тангенциальное, нормальное ускорение точки, а также радиус кривизны окружности:

Нормальное ускорение:

Радиус кривизны траектории:

Строим траекторию движения точки, на которой указываем положение точки М по ее координатам, а также векторы скорости, нормального, тангенциального и полного ускорения (рис.1.3.1).

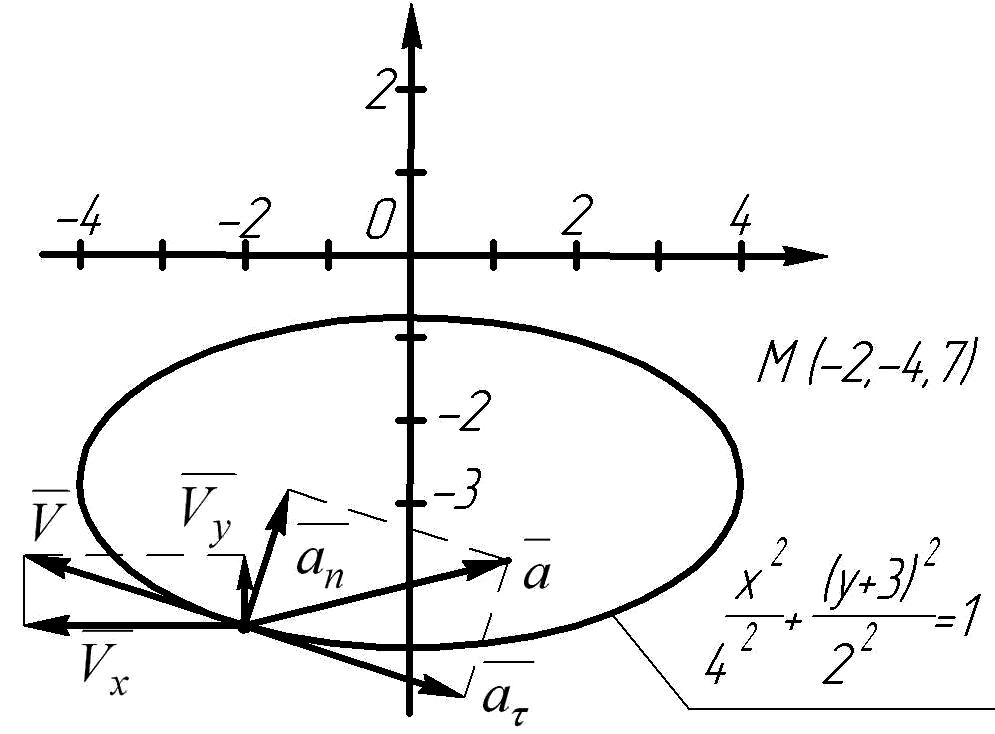
Рис.1.3.1