Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Муромский институт (филиал)

государственного образовательного учреждения

высшего профессионального образования

«Владимирский государственный университет»

Н.А. Лазуткина

Теоретическая механика

Раздел «Динамика»

Учебно-методическое пособие для проведения

программного контроля знаний студентов дневной и заочной форм обучения специальностей

151001.65 «Технология машиностроения»,

151003.65 «Инструментальные системы

машиностроительных производств»,

150900.62 «Технология, оборудование и автоматизация

машиностроительных производств»

Муром

2009

УДК 621.01 (075.8)

ББК 22.21+22.213

Л 17

Рецензент:

Кандидат технических наук, профессор кафедры «Технология машиностроения» МИ (филиала) ВлГУ

А.Н. Швецов

Печатается по решению редакционно-издательского совета

Муромского института (филиала)

Владимирского государственного университета

Л 17 Лазуткина, Н.А. Теоретическая механика. Раздел «Динамика»: учебно-метод. пособие для проведения программного контроля знаний студентов дневной и заочной форм обучения специальностей 151001.65 «Технология машиностроения», 151003.65 «Инструментальные системы машиностроительных производств», 150900.62 «Технология, оборудование и автоматизация машиностроительных производств» / Н.А. Лазут- кина. – Муром: Изд.-полиграфический центр МИ ВлГУ, 2009. – 112 с.: 14 ил. – Библиогр.: 5 назв.

ISBN 978-5-8439-0199-8

УДК 621.01 (075.8)

ББК 22.21+22.213

Учебное пособие написано в соответствии с утвержденными рабочими программами по курсу теоретическая механика и предназначено для проведения программного контроля знаний по дисциплине студентами технических специальностей.

Методическая разработка является дополнением к существующей литературе по курсу и улучшает методику освоения дисциплины.

ISBN 978-5-8439-0199-8

 Лазуткина Н.А., 2009

 Муромский институт (филиал)

государственного образовательного учреждения высшего профессионального образования

«Владимирский государственный университет», 2009

Введение

Законы и теоремы, лежащие в основе теоретической механики находят весьма разнообразное и обширное применение, поэтому у студентов, изучающих данный курс, наибольшее затруднение вызывает приложение общих положений теории к решению конкретных задач.

Данная методическая разработка ставит своей целью научить методам решения задач динамики.

Методическая разработка включают задания и методику решения типовых задач по разделу теоретической механики «Динамика» и включает следующие темы:

1. динамика точки;

2. колебание точки;

3. теорема о движении центра масс;

4. теорема об изменении количества движения;

5. теорема об изменении кинетического момента системы;

6. теорема об изменении кинетической энергии системы;

7. общее уравнение динамики;

8. определение динамических реакций подшипников;

9. уравнение Лагранжа второго рода.

Методическая разработка предназначена для подготовки студентов к проведению программного контроля знаний и является дополнением к существующей литературе по дисциплине «Теоретическая механика», поскольку улучшает ее методическое обучение и соответствует рабочим программам курсов всех форм обучения и рекомендуется к изданию через РИО МИ ВлГУ.

1 Примеры выполнения заданий

Пример 1.

Тело падает в сопротивляющейся среде с высоты под действием силы тяжести и силы сопротивления , пропорциональной квадрату скорости ( - постоянный коэффициент). С какой скоростью тело упадет на землю, если его начальная скорость ?

Решение.

На схеме (рис. 1) показаны начальное ( ) и текущее ( ) положение тела. Для начального положения тела показан вектор начальной скорости , для текущего – приложенные силы. Дифференциальное уравнение движения:

Рис. 1

.

Так как

,

то дифференциальное уравнение движения можно переписать в виде

.

Но

.

Поэтому:

;

или

.

Это уравнение является линейным относительно . Если обозначить , , , его можно привести к виду

.

Общее решение этого уравнения:

,

где - произвольная постоянная.

Возвращаясь к исходным обозначениям, имеем:

.

Начальное условие: при , . Поэтому:

, .

Следовательно:

.

Следовательно, при :

.

ПРИМЕР 2.

Лодка массой плавает в стоячей воде. На задней скамейке лодки, находящейся в покое, сидели два человека. Один из них, массой , перешел на нос лодки, пройдя по ней расстояние , другой, массой , переместился на среднюю скамейку на расстояние . На какое расстояние переместится при этом лодка?

При решении задачи людей считать материальными точками, сопротивлением воды пренебречь.

Решение.

Н

Рис. 2

а схеме (рис. 2) показаны внешние силы, действующие на механическую систему, состоящую из лодки и двух материальных точек, схематизирующих пассажиров лодки: силы тяжести , , и выталкивающая сила воды . Все внешние силы направлены по вертикали, их проекции на неподвижную горизонтальную ось Ох равны нулю. Поэтому дифференциальное уравнение движения центра масс С системы в проекциях на ось Ох будет:

,

или . Отсюда, интегрируя, находим . Значение постоянной интегрирования определяется из начального условия: при (так как вся система в начальный момент неподвижна). Тогда и . Интегрируя еще раз, получаем ( - координата центра масс системы при ).

По определению координата центра масс механической системы определяется выражением:

.

Поэтому из равенства следует или , или окончательно , где есть приращение координаты центра тяжести -го тела, входящего в систему, или, что то же, проекция его перемещения на ось Х.

В нашем случае абсолютные перемещения пассажиров и складываются из переносного перемещения вместе с лодкой и относительных по отношению лодки:

, .

Поэтому:

.

Отсюда:

.

Знак минус означает, что лодка перемещается против Х.

ПРИМЕР 3.

Г

Рис. 3

оризонтальная прямоугольная пластина АВДЕ со сторонами АВ=а=0,30 м, ВД=b=0,40 м и массой кг может вращаться без трения вокруг неподвижной вертикальной оси , проходящей через точку Е (рис. 3). На пластине имеется прямоугольный желоб АД, по которому может двигаться без трения груз массой кг.

В начальный момент пластина и груз неподвижны, и груз находится в точке А, затем груз начинает двигаться по пластине под действием внутренних сил по закону , м.

Определить угловую скорость пластины как функцию времени и найти ее значение в момент, когда груз окажется в точке Д.

Решение.

На схеме показаны внешние силы, действующие на систему пластина – груз: силы тяжести , и реакции , , , , подшипника и подшипника . Моменты каждой из этих сил относительно оси равны нулю. Поэтому по теореме об изменении кинетического момента . Отсюда . Постоянная интегрирования , так как в начальный момент система неподвижна. Следовательно .

Так как система состоит из двух тел – пластины и груза, то ее кинетический момент равен сумме кинетического момента пластины и момента количества движения груза: . Пластина вращается вокруг неподвижной оси, поэтому ( - проекция вектора угловой скорости на ось ).

Момент инерции пластины по теореме Штейнера:

.

При определении момента количества движения груза учитываем, что его движение сложное и абсолютная скорость равна геометрической сумме переносной и относительной скоростей.

По теореме Вариньона момент вектора относительно оси равен алгебраической сумме моментов его составляющих, поэтому момент количества движения груза равен сумме моментов векторов и :

.

Н

Рис. 4

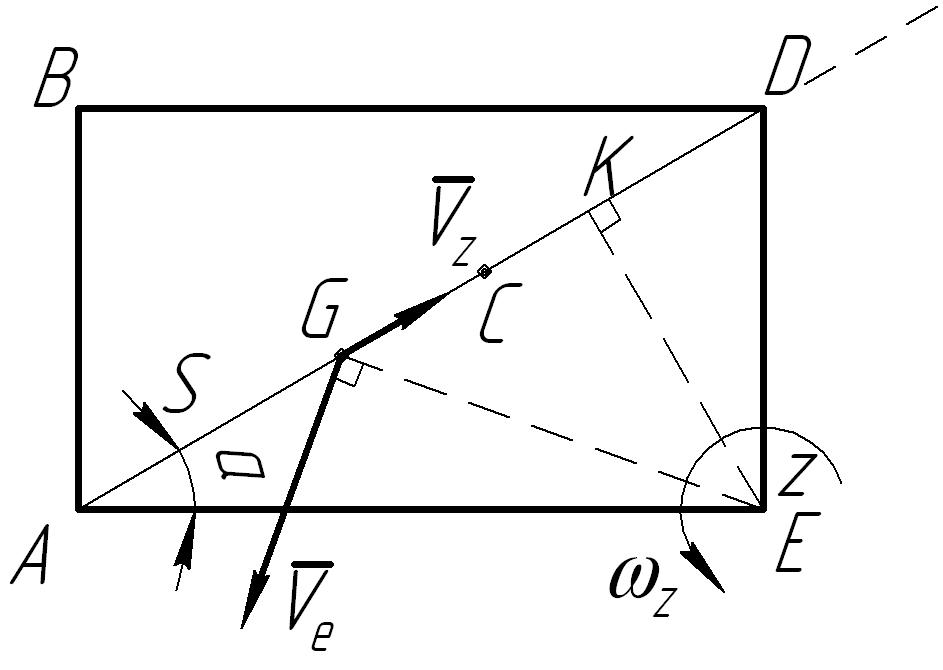
а рис. 4 вектор относительной скорости направлен в положительную сторону оси , что соответствует случаю, когда:

.

В этом случае отрицателен (точка движется по отношению к оси по часовой стрелке). Если будет (проекция на ось отрицательно), то направление будет противоположным и должен быть положительным. В обоих случаях справедливо равенство

.

Аналогично направление вращения пластины и переносной скорости показаны на рис. 4 для случая, когда . В этом случае и . Если же будет , то вектор будет направлен в противоположную сторону и равен по модулю ; момент количества движения будет равен:

.

Таким образом, и для момента вектора в обоих случаях ( и ) получили одинаковое выражение . Следовательно, при любых знаках величин и момент количества движения груза:

.

Вычислим и . Из . Из . Следовательно, . Из по теореме косинусов . Из . Поэтому .

Подставляя и в выражение для и прибавив к нему кинетический момент пластины, получим выражение для кинетического момента системы, который по доказанному ранее равен нулю:

.

После подстановки числовых значений получаем:

,

откуда

,

или

.

Чтобы определить значение в момент прихода груза в точку , замечаем, что в этот момент , или ; откуда с. При с получаем .

ПРИМЕР 4.

Рис. 5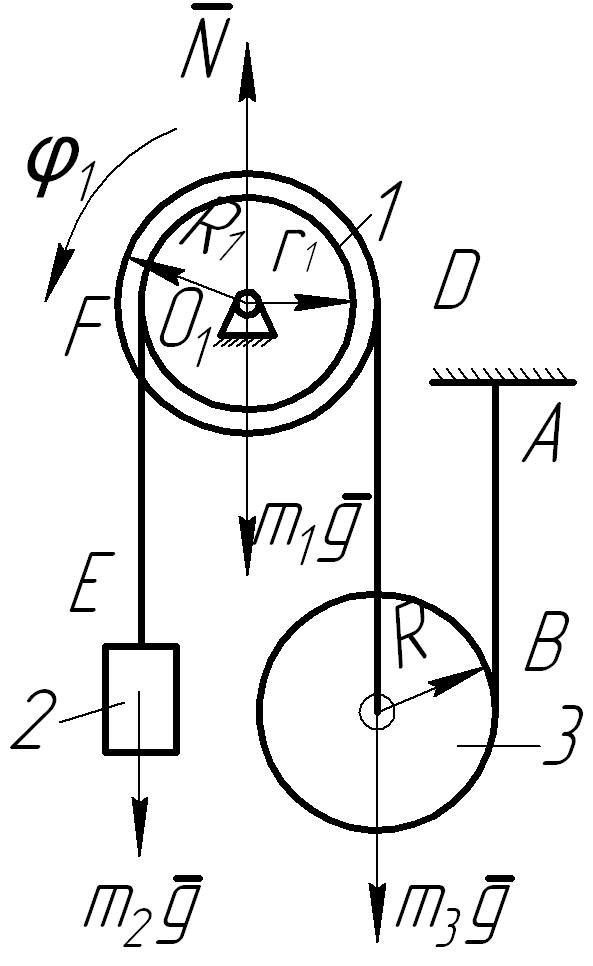

Ступенчатый шкив 1, имеющий массу и радиус инерции относительно оси вращения , обмотан гибкими нерастяжимыми нитями. К нити, сходящей со ступени радиуса прикреплен груз 2 массы . К нити, сходящей со ступени радиуса , шарнирно прикреплен цилиндр 3 в точке , лежащей на его оси. Этот цилиндр также обмотан нитью, конец которой закреплен в точке А. Участки и параллельны. Радиус цилиндра равен , а его масса - и равномерно распределена по его объему. Массы и радиусы удовлетворяют условию . Пренебрегая трением в шарнирах, определить угловую скорость ступенчатого шкива в функции угла его поворота, его угловое ускорение , натяжения нитей , , и реакцию оси . В начальный момент система неподвижна.

Решение.

Кинетическая энергия ступенчатого вала, вращающегося вокруг неподвижной оси:

.

Кинетическая энергия груза 2, совершающего поступательное движение:

.

Кинетическая энергия цилиндра, совершающего плоскопараллельное движение:

.

Мгновенный центр скоростей сечения цилиндра плоскостью чертежа находится в точке В (так как скорость участка нити АВ равна нулю).

Поэтому . Момент инерции цилиндра . Подставив эти выражения в формулу для , получим:

.

Учитывая, что , окончательно

.

Кинетическая энергия системы

.

При повороте ступенчатого шкива на угол груз опускается на величину , а ось цилиндра поднимается на . Сумма работ сил тяжести:

.

Другие силы, приложенные в данной системе, работы не совершают.

Так как в начальный момент система неподвижна, то по теореме об изменении кинетической энергии:

.

Это равенство и определяет зависимость от .

Чтобы найти угловое ускорение шкива 1, дифференцируем левую и правую части этого равенства по времени:

.

Так как , , то отсюда получаем:

.

Ч

Рис. 6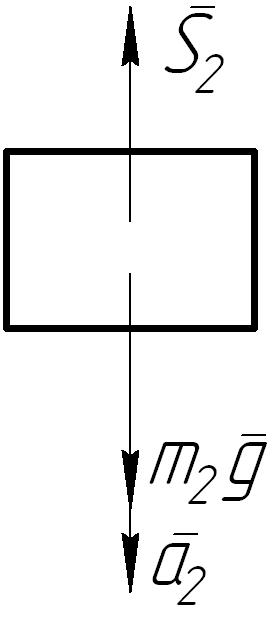

тобы определить натяжение нити , напишем уравнение второго закона Ньютона для груза 2, к которому приложены силы и (рис. 6):

,

где - ускорение груза.

Отсюда

Рис. 7

.

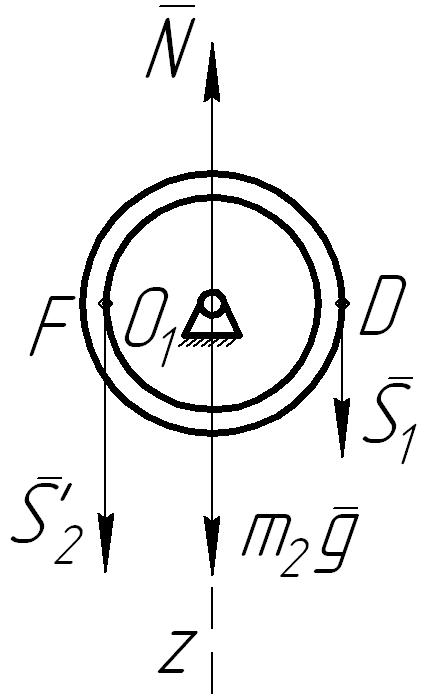
Для определения натяжения нити применим к ступенчатому шкиву дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. К шкиву приложены силы , , , (рис. 7). Поэтому

.

Так как , то отсюда

.

Для определения реакции применим к шкиву теорему о движении центра масс:

.

Так как , то

Рис. 8

.

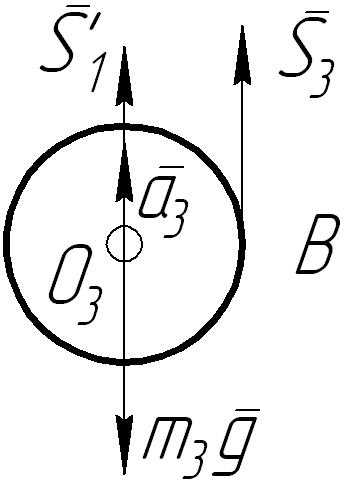
Наконец, для определения натяжения нити АВ применим теорему о движении центра масс к цилиндру 3, на который действуют внешние силы , , (рис. 8):

.

Так как , то отсюда

Подставив сюда выражение , получим .

ПРИМЕР 5.

П

Рис. 9

Рис. 10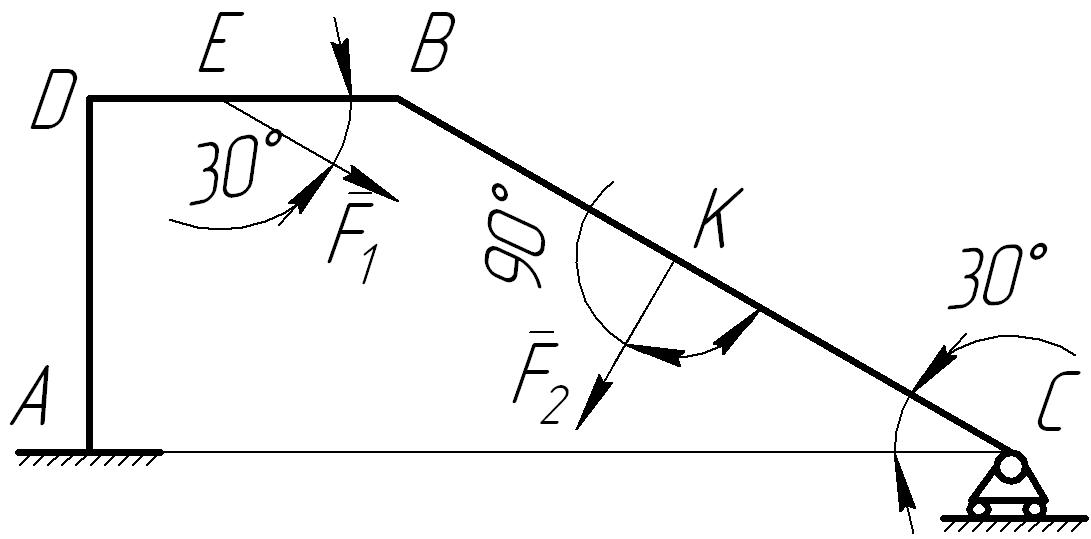

ользуясь принципом возможных перемещений, определить для составной конструкции, изображенной на схеме (рис. 9), реактивный момент и вертикальную составляющую реакции заделки, если . , , м, кН, кН.

Решение.

Для определения реактивного момента заменим заделку в точке А шарнирно-неподвижной опорой, компенсировав отброшенную связь ее реакцией – реактивной парой сил с неизвестным моментом (рис. 10).

Получившейся механической системе с одной степенью свободы даем возможное перемещение, повернув мысленно уголок АДВ на бесконечно малый угол , например по часовой стрелке. Точка В получит при этом возможное перемещение , направленное перпендикулярно АВ и равное по модулю ; точка С получит возможное перемещение , параллельное опорной плоскости шарнирно-неподвижной опоры С; стержень ВС повернется вокруг точки L – центра поворота, определенного как и МЦС в кинематике, как точка пересечения перпендикуляров, проведенных через точки В и С к направлениям их возможных перемещений. Угол , на который стержень ВС повернется вокруг точки L, определяется равенством:

, откуда

.

Для нахождения воспользуемся теоремой синусов. Из (см. рис. 10):

.

Отсюда:

.

Следовательно,

.

Теперь подсчитаем и приравняем к нулю сумму работ сил , и пары с моментом при возможном перемещении системы.

Используя правило: работа сил, приложенных к вращающемуся телу, равна взятому с соответствующим знаком произведению момента сил относительно оси вращения на угол поворота. Поэтому:

.

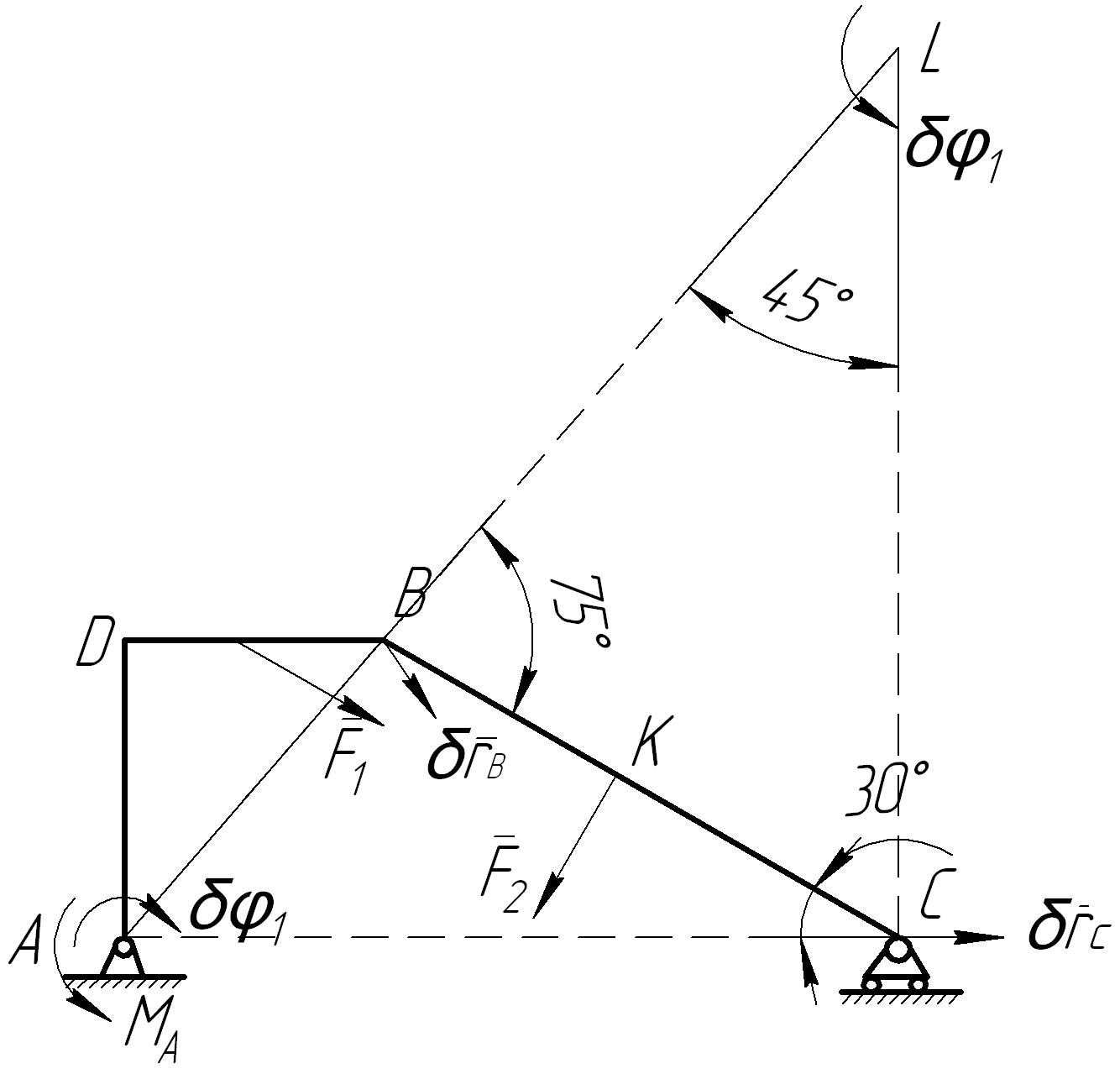
З

Рис. 11

десь в первых скобах записана сумма моментов силы и реактивной пары относительно точки А. Для определения момента силы она была разложена на вертикальную и горизонтальную составляющие. Со знаком плюс записаны моменты, направленные в сторону поворота . Момент пары записан со знаком минус, так как она стремится вращать уголок в направлении, противоположном возможному перемещению . Во вторых скобках записано плечо силы относительно точки L. Знак минус перед второй скобкой поставлен потому, что сила стремится вращать стержень ВС вокруг точки L в направлении противоположном возможному перемещению .

Заменяя в предыдущем равенстве его выражением через и учитывая, что , , можем переписать его в виде:

.

Так как , то отсюда:

кНм.

Для нахождения вертикальной составляющей реакции заделки А заменим в исходной схеме заделку ползуном, который может перемещаться в вертикальном направлении и к которому жестко прикреплен угол АДВ, а отброшенную связь компенсируем вертикальной реакцией (рис. 11).

Даем получившейся механической системе возможное перемещение, мысленно переместив угол АДВ поступательно вверх ( ). Стержень ВС повернется вокруг центра поворота G на угол . Уравнение принципа возможных перемещений запишется в виде:

,

откуда, учитывая, что , , , получаем

кН.

ПРИМЕР 6.

Сплошной однородный цилиндр 1 массой кг и радиусом м может вращаться без трения вокруг неподвижной горизонтальной оси . С цилиндром жестко скреплены тонкие однородны стержни 3 и 4 массой и длиной

Рис. 12

каждый. В середине В стержня 4 к нему прикреплена нить, перекинутая через невесомый блок 2 и намотанная на цилиндр 5, одинаковый с цилиндром 1. При движение системы ось цилиндра 5 перемещается по вертикали. В точке Д к стержню 3 прикреплена пружина жесткостью кН/м. В начальном положении системы стержень 3 и участок нити между стержнем и блоком расположены горизонтально, а стержень 4 и ось пружины – вертикально; пружина растянута на величину .

Начальные значения обобщенных координат и равны нулю, а обобщенных скоростей - , . Трением в осях , , массой пружины и нити пренебрегаем.

Используя уравнение Лагранжа II рода, найти кинематические уравнения движения системы при малых отклонениях цилиндра 1 от начального положения и определить круговую частоту и период колебания системы.

Решение.

Кинетическая энергия системы равна сумме кинетических энергий вращающегося цилиндра 1 с жестко присоединенными к нему стержнями и цилиндра 5, совершающего плоскопараллельное движение:

.

В этом выражении - момент инерции цилиндра относительно его оси; - момент инерции стержня; в квадратных скобках – момент инерции цилиндра 1 с жестко присоединенными к нему стержнями.

Скорость центра цилиндра 5 равна сумме скорости точки нити и скорости точки во вращательном движении вокруг полюса .

Д

Рис. 13

ля определения рассмотрим положение системы, при котором цилиндр 1 и стержни 3 и 4 отклонены от начального положения на угол (рис. 13). Скорость точки нити равна скорости точки Е, в которой участок нити ВЕ касается блока 2. Так как нить нерастяжима, то проекция скоростей точек В и Е на направление нити равны. Поэтому:

.

Теперь воспользуемся малостью отклонений стержней от начального положения. Как известно, функция и можно разложить в ряды Маклорена:

;

.

При «малых» (до 0,1 радиана) значения и отличаются от первых членов соответствующих разложений менее чем на 0,5%. Поэтому можно принять , . Так как при «малом» угол также является «малым», то . Поэтому в этом случае

, тогда .

Подставляя в ранее написанное выражение для Т, после простых преобразований приводим его к виду:

.

Для нахождения обобщенных сил и , соответствующих обобщенным координатам и , вновь обратимся к рис. 13. Чтобы определить , дадим мысленно системе возможное перемещение, при котором обобщенная координата изменяется на бесконечно малую величину , а обобщенная координата не изменяется. В этом случае точка В получит возможное перемещение , направленное по вектору . Такие же по абсолютному значению перемещения при «малых» получат точки Е, G, К и . Поэтому сила тяжести цилиндра 5 совершит работу . Работа сил тяжести стержней и силы упругости пружины равна произведению их момента относительно оси вращения на угол поворота , т.е.

.

Из рис. 13 видно (см. ), что

.

При . Этот результат означает, что угол является малым более высокого порядка, чем (имеет порядок квадрата ), и по сравнению с им можно пренебречь. Тогда сумма работ всех задаваемых сил при повороте цилиндра 1 на угол будет:

.

Укорочение пружины, соответствующее положению цилиндра 1, повернутому из начального положения на угол , равно разности . Длина укоротившейся пружины равна

,

или при «малых» :

.

Следовательно, укорочение пружины

.

Так как в начальный момент пружина была растянута на величину , то ее растяжение уменьшается и станет , а упругая сила будет .

Обобщенна сила, соответствующая углу :

,

или окончательно

.

Для нахождения обобщенной силы , соответствующей обобщенной координате , нужно сообщить системе возможное перемещение, при котором останется неизменным, а увеличивается на бесконечно малую величину . В этом случае работу совершает только сила тяжести цилиндра 5: .

Обобщенная сила:

.

Теперь составим уравнение Лагранжа:

, .

Частные производные:

; .

, .

Уравнение Лагранжа будет иметь вид:

;

.

Из второго уравнения после сокращения его на :

.

Подставив это выражение в первое уравнение, после простых преобразований получим:

.

Обозначим:

.

Величина:

1/с

и представляет искомую круговую частоту колебаний.

Период колебаний:

с.

Общее решение дифференциального уравнения малых колебаний цилиндра:

есть функция:

.

Для нахождения постоянных интегрирования и используем начальные условия: при , , (1/с).

Из первого условия следует ; из второго условия, учитывая, что:

,

получаем ; . Поэтому окончательно:

.

Для нахождения интегрируем ранее полученное уравнение:

.

Имеем:

.

Из начальных условий: при , , следует ; . Тогда:

.

Интегрируя еще раз, получаем:

.

Из начальных условий: при , , следует . Поэтому:

.

После подстановки числовых значений:

.

ПРИМЕР 7.

В

Рис. 14

ывести кинематические уравнения движения системы, показанной на рис. 14, пренебрегая массой пружины. Качение катка происходит без проскальзывания. Трением в оси пренебречь. Блок и каток – одинаковые цилиндры радиусом м и массой кг, равномерно распределенной по их объему. Жесткость пружины Н/м.

Начальные значения обобщенных координат и равны нулю; начальное удлинение пружины ; начальные значения обобщенных скоростей м/с, .

Решение.

Кинетическая энергия системы:

.

Обобщенные силы:

, ,

где - сила упругости пружины.

Уравнение Лагранжа для рассмотренной системы:

; .

Сила упругости зависит от деформации пружины, которая равна , где - начальное значение деформации. Обозначим . Тогда ; . С другой стороны, дифференциальные уравнения движения системы можно представить в виде:

; .

Вычитая из первого уравнение второе, получаем

,

или

.

Подставляя заданное значение , получим:

, где .

Решением этого дифференциального уравнения при начальных условиях: при , , является функция: . Тогда .

Дифференциальные уравнения движения системы принимают вид:

;

.

Интегрируя эти уравнения при начальных условиях: , , , , , получим:

;

;

;

.

После подстановки численных значений получим:

;

.