1.4. Адиабатические процессы в атмосфере

Адиабатическими называются процессы, происходящие без обмена теплом с окружающей средой. Применительно к метеорологии эти процессы происходят в атмосфере, но соблюдаются не в полной мере строго, поскольку теплообмен с окружающими массами воздуха всегда существует. Однако, если процесс происходит достаточно быстро, то влиянием теплообмена можно пренебречь.

Если некоторая масса воздуха адиабатически расширяется, то в ней снижается давление и температура. При адиабатическом сжатии давление и температура возрастают. Эти изменения происходят вследствие изменения внутренней энергии газа, величина которой прямо пропорциональна его абсолютной температуре. При рассмотрении некоторого объема воздуха вполне допустимо считать его идеальным газом, к которому применимо уравнение Пуассона

, (1.17)

где dQ – изменение количества тепла;

C_VdT – изменение внутренней энергии газа;

PdV – работа расширения или сжатия;

C_v – удельная теплоемкость газа при постоянном объеме;

P – давление;

T – температура газа;

V – удельный объем.

Поскольку в адиабатическом процессе dQ = 0, то

C_vdT = –PdV (1.18)

Уравнение (1.18) содержит значение dV. Величина удельного объема газа не может быть измерена непосредственно. Для того, чтобы исключить ее, необходимо использовать уравнение состояния атмосферы (1.1) PV = RT. После дифференцирования его получим PdV+VdP = RdT, откуда PdV=RdT–VdP, из уравнения состояния атмосферы , следовательно

(1.19)

С учетом полученного значения для PdV уравнение (1.18) примет вид:

, или

, т.е.

(1.20)

Удельные теплоемкости газа при постоянном объеме C_v и при постоянном давлении C_p связаны между собой соотношением C_p=R+C_v, откуда

(1.21)

или

(1.22)

Проинтегрировав это выражение от начальных параметров T₀ и P₀ до конечных T и P

, (1.23)

получим

. (1.24)

Закон, по которому происходят адиабатические изменения в идеальном газе, с достаточной степенью точности применим как к сухому, так и к влажному воздуху.

Для сухого воздуха постоянные величины, входящие в формулу (1.24) имеют следующие значения R_d=287 Дж/кгК, C_v=718 Дж/кгК и C_p=1005 Дж/кгК, следовательно , откуда .

В атмосфере расширение воздуха и падение его давления происходит, как правило, при его восходящем движении. В этом случае выполняется работа расширения, производимая за счет внутренней энергии газа, т.е. кинетической энергии молекул. Такое изменение выражается в понижении температуры воздушной массы и падении давления. При нисходящем движении воздушной массы ее сжатие происходит за счет работы внешних сил, т.е. работы сжатия. В этом случае возрастает внутренняя энергия газа, что выражается в увеличении температуры давления воздуха.

Уравнение (1.21) можно записать в виде

(1.25)

где индекс i обозначает, что температура относится к поднимающейся или опускающейся индивидуальной частице воздуха. Из основного уравнения статики атмосферы имеем

(1.26)

где: T_a – температура в атмосферном столбе.

Подставив значение в уравнение (1.25), получим

, откуда

Поскольку температура индивидуальной частицы воздуха всегда близка температуре атмосферного столба, то соотношение близко к единице. Тогда

(1.27).

При g=9,81 м/с² и C_p=1005 Дж/кгК .

Таким образом, при адиабатическом подъеме температура воздуха уменьшается на 1ºС на каждые 100 м высоты, а при опускании на такую же величину возрастает. Полученное значение относится к сухому, а также к влажному, но ненасыщенному воздуху. Эта величина называется сухоадиабатическим градиентом и обозначается .

В процессе адиабатического подъема влажного, но ненасыщенного воздуха его относительная влажность увеличивается, и воздух приближается к насыщенному состоянию. Насыщение наступает на высоте, называемой уровнем конденсации. При дальнейшем подъеме насыщенный воздух охлаждается иначе, чем ненасыщенный. В насыщенной массе воздуха происходит конденсация водяного пара, в процессе которой выделяется теплота в количестве 2,50110⁶ Дж/кг. Выделение этой теплоты замедляет падение температуры воздуха при его подъеме. В поднимающемся насыщенном воздухе его температура падает по влажноадиабатическому закону с влажноадиабатическим градиентом .

При атмосферном давлении 1000 гПа на каждые 100 м подъема насыщенный воздух при температуре -20ºС охлаждается на 0,88ºС, при 0ºС – на 0,66ºС, а при 20ºС – на 0,44ºС. При понижении температуры воздуха влажноадиабатический градиент приближается к сухоадиабатическому ввиду малого содержания в нем водяного пара и, следовательно, малого количества выделяемого тепла. В табл. 1.4 приведены величины влажноадиабатического градиента температуры для различных значений давления и температуры воздуха.

Таблица 1.4

Значения для некоторых P и t

Давление, гПа	Температура, ºС
	-20	-10	0	+10	+20
1000	0,88	0,78	0,66	0,54	0,44
900	0,86	0,76	0,64	0,52	0,42
700	0,83	0,72	0,59	0,47	0,38
500	0,77	0,64	0,52	0,41	0,33

При опускании воздушной массы, если в нем отсутствуют продукты конденсации, то эта масса перейдет в ненасыщенное состояние. В этом случае при дальнейшем опускании ее температура будет в соответствии с сухоадиабатическим градиентом на 1ºС на каждые 100 м высоты.

Если же в нем содержатся капли воды или кристаллы льда, то они будут испаряться, и воздух будет оставаться насыщенным до тех пор, пока все продукты конденсации не перейдут в газообразное состояние. Температура воздуха в этом случае будет повышаться в соответствии с влажноадиабатическим процессом.

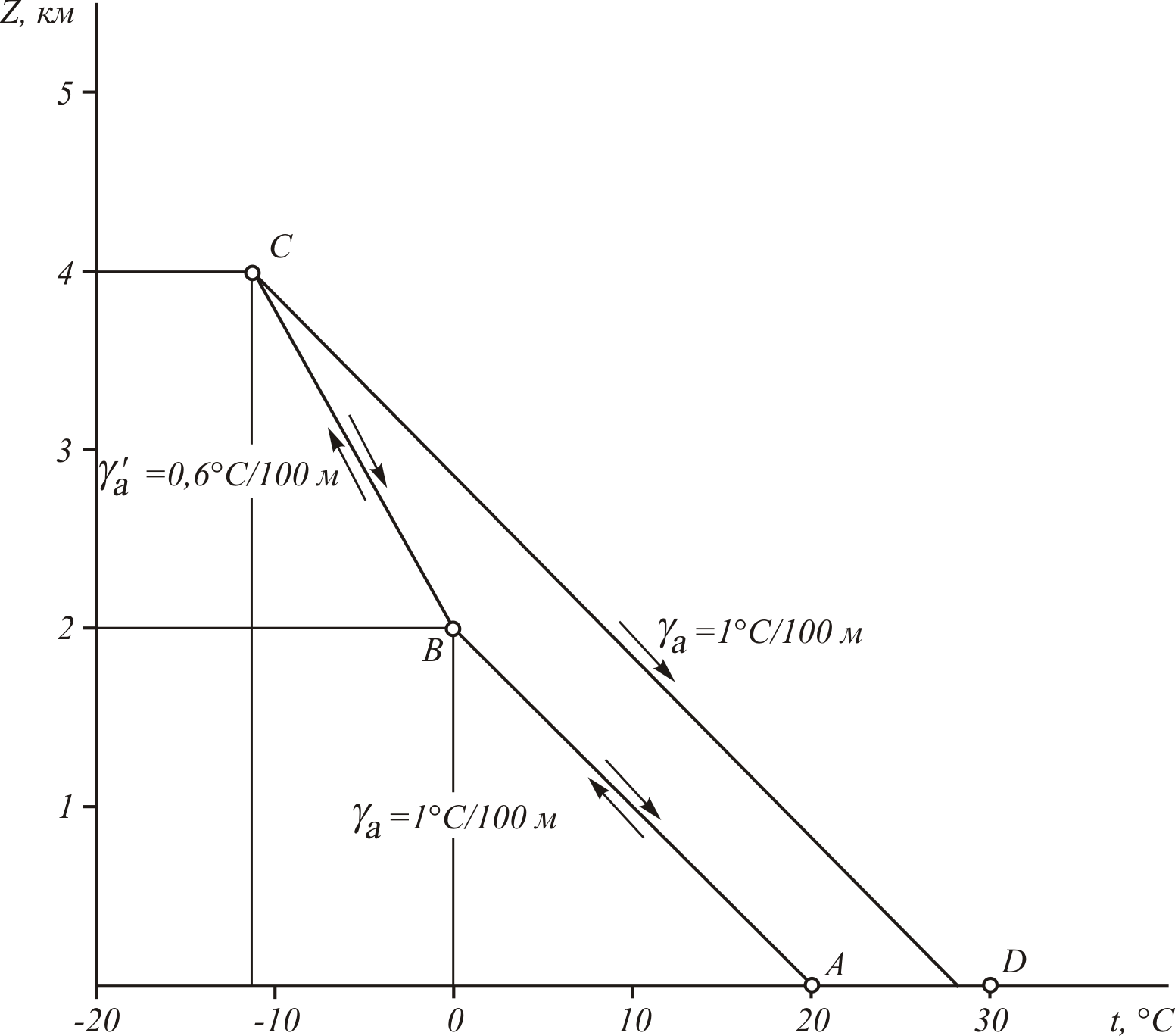
Рис. 1.5. Адиабатические и псевдоадиабатические процессы

Предположим, что некоторая масса влажного ненасыщенного воздуха, находящаяся на уровне моря, при давлении 1000 гПа, имеет температуру +20ºС (т.A на рис. 1.5). При подъеме до высоты 2000 м температура в ней будет снижаться по сухоадиабатическому закону с градиентом γ_a=1ºС/100 м.

Допустим, что высота 2000 м соответствует уровню конденсации. В этом случае рассматриваемая масса воздуха на этой высоте будет иметь температуру 0ºС при давлении 800 гПа (т. В на рис. 1.5). При дальнейшем подъеме воздушной массы ее температура будет снижаться по влажноадиабатическому закону с градиентом /100 м. На высоте 4000 м она снизится до -12ºС (т. С на рис. 1.5).

Если продукты конденсации сохранились в атмосфере, то при опускании рассматриваемой воздушной массы до высоты 2000 м ее температура возрастет до 0ºС и достигнет т. B на рассматриваемом графике, поскольку воздух на этом участке остается в насыщенном состоянии.

При дальнейшем снижении воздух будет находиться в ненасыщенном состоянии и его температура будет повышаться на 1ºС на каждые 100 м потери высоты. Таким образом, на уровень моря рассматривая воздушная масса возвратится при той же температуре +20ºС, при которой она начала свое движение вверх.

Если до начала опускания воздушной массы продукты конденсации, находившиеся в ее более низких слоях, выпали в виде осадков, то в процессе ее снижения температура воздуха будет возрастать по сухоадиабатическому закону с градиентом γ_a =1ºС /100 м . В этом случае при опускании до уровня моря масса воздуха приобретет температуру +28ºС (т. D на графике), что на 8ºС больше той температуры, при которой эта воздушная масса начала свое движение вверх.

Очевидно, что за рассматриваемый период в массе воздуха произошел необратимый термодинамический процесс. В метеорологии такой процесс называется псевдоадиабатическим.

Если воздух, находящийся в атмосфере на некоторой высоте Z имеет давление P при температуре T, то при его опускании на уровень, где атмосферное давление равно Р₀, он приобрел бы температуру .Температура, которую приобрел бы воздух при давлении P₀=1000 гПа, называется потенциальной температурой. Ее величина определяется уравнением Пуассона

.

Приближенно потенциальную температуру воздуха можно рассчитать по формуле .

Если воздушная масса, находящаяся на высоте 3000 м имеет температуру -20ºС, то ее потенциальная температура, в соответствии с изложенной в предыдущем абзаце зависимостью, будет на 30ºС выше и составит +10ºС. Использование понятия потенциальная температура, позволяет сравнивать между собой состояние воздушных масс, находящихся на различной высоте.

При изменении состояния массы воздуха по сухоадиабатическому закону его потенциальная температура не изменяется, поскольку и при подъеме и при опускании воздуха изменение его температуры составляет 1ºС на каждые 100 м изменения высоты. При нисходящем движении температура воздушной массы повышается, а при восходящем понижается на 1ºС на каждые 100 м. Если же в процессе подъема воздушной массы происходит конденсация водяного пара, то ее потенциальная температура возрастает.

Изменения температуры в элементарной частице воздуха, адиабатически поднимающейся или опускающейся, не следует смешивать с распределением температуры по высоте в атмосфере.

Температура в атмосферном столбе воздуха может изменяться по различным законам в зависимости от типа процессов, происходящих в этом столбе. График фактического изменения температуры с высотой в определенный момент времени называется кривой стратиграфии. Характер кривой стратиграфии определяется вертикальным градиентом температуры , обычно за единицу приращения высоты dZ принимается 100 м.

При падении температуры с высотой вертикальный градиент имеет положительное значение, если же температура воздуха с высотой возрастает, то ее градиент становится отрицательным.

В реальной атмосфере изменение температуры воздуха с высотой носит достаточно сложный характер. Если температура воздуха с высотой не изменяется, то такое явление называется изотермия. Если же температура воздуха с высотой возрастает, то имеет место инверсия температуры.

В тропосфере, т.е. в нижних слоях атмосферы на высоте от 10 до 11 км в обычных условиях для умеренных широт =0.65ºС/100 м. В нижних сотнях метров градиент температуры возрастает до 10ºС/100 м, а в тонком приземном слое над нагретой почвой он может превосходить 10ºС/100 м.

В стратосфере, на высоте от 10 до 50 км преобладают инверсионные и изотермические слои. Такие же слои возникают при определенных условиях в тропосфере и даже в ее приземном слое.

В зависимости от стратификации атмосферы потенциальная температура поднимающейся массы воздуха изменяется в соответствии с измерением температуры окружающей среды. Если γ=1ºС/100 м¸ то потенциальная температура не изменяется с высотой. Если γ<1ºС/100 м, что является наиболее распространенным явлением в атмосфере, то потенциальная температура возрастает тем в большей степени, чем меньше величина градиента температуры.

В изотермическом слое при =0ºC/100 м потенциальная температура возрастает на 1ºС/100 м увеличения высоты.

В слое инверсии, где вертикальный градиент температуры 0ºС, потенциальная температура возрастает в еще большей степени, чем в изотермическом слое. Это возрастание пропорционально разности температурного и адиабатического градиентов.

Только в том случае, если вертикальный градиент температуры в воздушном столбе превышает 1ºС/100 м, потенциальная температура восходящей массы воздуха уменьшается.