
- •Міністерство аграрної політики та продовольства україни львівський національний аграрний університет
- •Завдання для виконання контрольної роботи з курсу “Інформатика і програмування”, студентами факультету заочної освіти
- •Завдання 3 Редактор формул Equation Editor. Створення рисунків у редакторі Word.
- •Завдання 4 Табулювання функції. Побудова графіків.
- •Завдання 5 Розрахунок точкового прогнозу на основі трендового аналізу
- •Використання функцій для роботи з посиланнями та масивами. Елементи лінійної алгебри
- •Завдання 7 Створення рекламної презентації населеного пункту засобами Microsoft Power Point».
- •Завдання 8. Комп’ютерні мережі. Інтернет. Пошук інформації. Розмови в Інтернет.
- •Вихідні дані до завдання 6
Завдання 3 Редактор формул Equation Editor. Створення рисунків у редакторі Word.
Опрацювати типові операції по набору формул в редакторі формул Equation Editor;
оволодіти навичками створення рисунків середньої складності в текстовому документі.
Запустити редактор Word з меню “Пуск” або піктограмою на робочому столі.
Вставити об’єкт Equation Editor до документу Word (“Вставка объекта”).
В пункті “Определить” меню “Размер” задати розмір різних елементів формул згідно з таблицею:
Текст |
Times New Roman Cyr |
курсив |
Функція |
Times New Roman Cyr |
курсив |
Змінна |
Times New Roman Cyr |
курсив |
Рядковий грецький |
Symbol |
курсив |
Символ |
Symbol |
рядковий |
Матриця-вектор |
Times New Roman Cyr |
курсив |
Числа |
Times New Roman Cyr |
рядковий |
В пункті “Определить” меню “Стиль” задати шрифти та їх вигляд для різних елементів формул згідно з таблицею
Звичайний |
11пт |
1B p X k p 1 nk |
Крупний індекс |
9 пт |
|
Дрібний індекс |
7 пт |
|
Крупний символ |
15 пт |
|
Дрібний символ |
11 пт |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Набрати систему лінійних алгебраїчних рівнянь n–го порядку у матричному вигляді і у вигляді окремих рівнянь. Невідомі xi (i=1,…,n), коефіцієнти матриці aij = i/j (j=1,…,n), елементи стовпчика правої частини bi=i/5. Число n обирається згідно за номером у списку в журналі групи: для непарних n=3, для парних n=4. При наборі цих формул зручно використовувати операції копіювання.




 Набрати
формули
згідно
з власним
номером
у списку
в журналі
групи.
Набрати
формули
згідно
з власним
номером
у списку
в журналі
групи.
1 |
T (x , Fo) N N 1 0 x x R R,1 T (x , Fo) T (x , Fo) 1 1 x1 0 xR T( x, Fo) T1 ( x1 , Fo) x 1 x f 2 (Fo) xR 1 x1 01 |
2 |
l l сh p 1 R* p sh p 1 1 1, 1 1 * sh p 1 R* p ch p 2,1l 1 1, 1 1 1 |
3 |
T ( x,Fo) m ( ( x),)H( n )( Fo)H l( pk ) ( p ,( x))exp(2Fo) n n,l n l ' Q k n,l l1n0 k1(n ,pk ) z*( x,Fo). |
4 |
F ( p ) F ( p )сh p 1 1 R1, p 1 sh p 1 * 1, 2 ,1 F ( p )sh p 1 1 R1 p 1 ch p 1 * * ,1 , 2 |
5 |
H 0 ( p ) h Bi f ( p ) h Bi M z* ( 0, p ) z*' (1, p ); 0 0 0 0 0 0 1 0 1 H 1( p ) h Bi f ( p ) p F* ,m1( p ) h Bi M F ( p ). 1 1 1 1 m m 1 1 1 m,m1 |
6 |
Fo n n Fo 2n z * ( x ,Fo ) n ( 2n ) ( x ) * ( Fo )n W ( x ,)d 2n n 0 n! n 0 n! 0 x |
7 |
1 [ m1 / 2 ] ( 2 j 1)! m ( Fo ) a jk Fo jk ( x ) a x k ,2k 1 ( 2k 1)! ( j k )! ,2 j1 ,k j k k 0 |
8 |
m * [ m / 2 ] ( 2 j )!( 2 j )! w ( x,Fo ) a* Fo j x j ( Fo) a* jk Fo3 jk 1 , j ,2k ,2 j j0 ( 2k )! jk ( 3 j k 1)! |
9 |
( x ) n a ( x ) 1 n1 a* ( x )* n ,1 nj , , j 1, 1 n j 1, , j j 0 j0 n a ( x ) n a* ( x )* 1 1, , nj , , j n j , , j j 0 j0 |
10 |
() f (), () f (), L, () f ( N ) 1 2 n ( ) k1 ()k1 f f ()d, f ( k ) f ( k ) ()d ( ) () 1 () ( 0 ) k 0 0 ! 0 ( k 1)! |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
11 |
( p ) 1 1 2 sin2 1 2 sin2 1 2 k 1,2 1 k 1 1,2 1 k , k 2 1 1 1 1 1 x 2n 1,n ( x ) ( 2n )! n , 1 |
12 |
1 1 2i 2i i ( 2 y )! i 1 1,2 1 1 1,2 1 , 2 2 2 1 2 1 a1 , 1,2 a 2 2 |
13 |
x 2 x 4 x 2 N x 2 3 ( x,) f2 ,э () 2! 1 () 4! 2 () K ( 2N )! n () g2 () 3 x 4 x 6 x 2 N 2 * () * () K * (), 3! 1 5! 2 ( 2N 1)! N 3 3 3 |
14 |
* t u v * ( n 1 1 1 div( ))dxdydt 1 1 1 0 t x y t* N Q ( x x )( y y )( t t )* dxdydt. і і і 0 1 0 і 1 |
15 |
( k ) 3 ( k ) ( k ) 2 Pw( k ) ( k ) 3 P ( u( k ) v( k ) ) x Pmum ,x , z m m1 , xy m m,y m,x m0 m1 m0 ( k ) 3 ( P w( k ) Pu( k ) ) xz m m1,x m m m0 |
16 |
t 2 t , x E2 t * x 2 t , x 2 , x R t * x ,* x d; (1) *x c 1 t , x 1 t , x , 1 1 t x 1 x |
17 |
1 B e 1 0 B x j t , x ср – 2 e B 1 a j t k B e B1 2 l a j t k B 1 1 1 B ср e 1 0 B x , e B1 2 l a j tk B - e B1a j tk B ср 1 1 |
18 |
vx wz z0 b zz0 2 a2 b z z0 2 a2 x, y ,z Q e 2 D 2 Dz e e 2D 4 z z 2 a 2 z z 2 a 2 0 0 K a b2 2 sinz z0 1 cosz z0 d. 1 0 2 2 0 1 |
![]()
![]()
![]()
![]()
19 |
0 0 0 pl t pl t x2 p p 1 U0 V0 dt, h1 1 tg V0dt l l 0 0 0 t h0 h0 V0dt 0 |
20 |
n1
u1
1
,1
,1 i1 n1 v2 2 ,2 u0 tg vi 22 P2i1 2 i1 |
21 |
dh1 dx2 1i 1i 1 ,1 , Re, h1 , x2 , d, d, i 1, 2, ..., 9, ,, Re, h , x , dh1 , dx2 , i 1, 2, ..., 7, 2i 2i 2 2 1 2 d d |


 Збережіть
зроблені зміни.
Збережіть
зроблені зміни.Вставити рисунок до документу, використовуючи меню “Вставка” пункт “Объект”,
елемент списку “Рисунок Microsoft Word”.
За допомогою піктограми в нижній частині екрану зобразити координатні осі Ох та Оу. Збільшити їх товщину, змінити тип стрілки та шаблон лінії за допомогою пунктів вкладки “Цвета и линии” вікна, що з’являється після подвійного натиснення миші на об’єкт.
Зробити підписи осей (піктограма ): х та у, задавши для поточного шрифту розмір 12 pt, курсив. Вилучити рамку з підпису (вкладка “Цвета и линии”, пункт “Нет линий” параметру “Линии”). Встановити нульову відстань від області тексту до зовнішньої границі рамки (вкладка “Надпись”).
Провести відрізок прямої через початок координат, І та ІІІ квадранти. При необхідності точно вказати положення відрізка (кнопка “Дополнительно” вкладки “Положение”).
Показати стрілкою дугу кута, що утворився між відрізком та позитивним напрямком осі Ох. Стрілка повинна мати вказівними з обох кінців (пункт “Стрелки” вкладки “Цвета и линии”). Зробити підпис “” аналогічно п. 5.
Викривити нарисовану стрілку, використовуючи пункт “Начать изменение узлов” контекстного меню. При цьому потрібно додати вузли та вказати сегменти, які треба викривити.
Розширити площу, яку займає рисунок, перемістивши обмежувачі на розмічених полях з правого та нижнього боків при натиснутій кнопці миші.
На вільному місці рисунку зобразити паралелепіпед (меню “Автофигуры”, пункт “Основные фигуры”, елемент списку ”Куб”). Змінити відношення його сторін, переміщуючи кольоровий маркер мишею, який з’являється, якщо об’єкт обрано.
Створити циліндр (меню “Автофигуры”, пункт “Основные фигуры”, елемент списку ”Цилиндр”). Аналогічно попередньому пункту змінити пропорції зображеної фігури.
Повернути паралелепіпед та циліндр на заданий ненульовий кут (пункт “Поворот”
вкладки ”Размер”).
Нарисувати незамкнену полілінію на менш ніж з 5 сегментів (меню “Автофигуры”, пункт “Линии”, елемент списку ”Полилиния”). Змінити шаблон лінії, викривити два довільних сегмента (див. п. 8). Замкнути полілінію, обравши пункт контекстного меню.
Заповнити кольором область, обмежену створеною полілінією. Використовувати пункт “Способы заливки” меню “Цвет” вкладки “Цвета и линии”: “Градиентная”, “Текстура”, “Узор”.
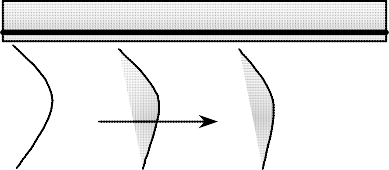
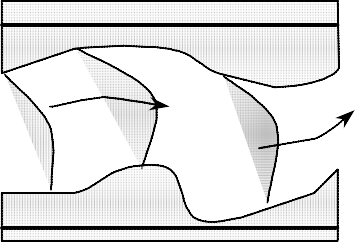
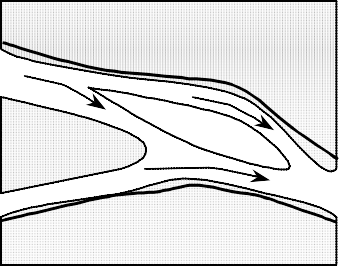
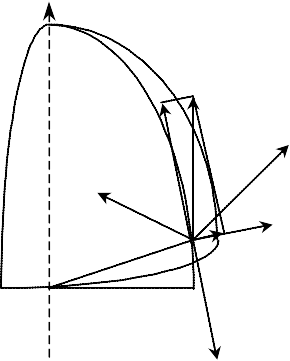 Створити
один
з рисунків
згідно
свого
варіанту:
Створити
один
з рисунків
згідно
свого
варіанту:
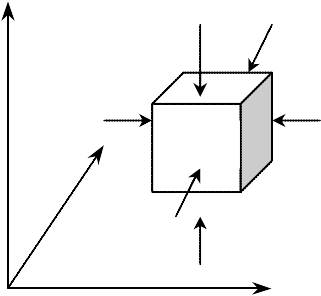 G+Pz+dPz
G+Pz+dPz
z
Py+dPy
Px Px+dPx
x y
1. 2.
y dz
dy
Py dx
Pz
x
c
z
z
x
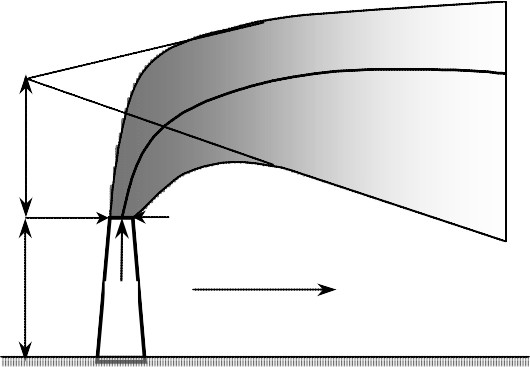 H
H
R0 (vx)x
u
(vz)z+dz
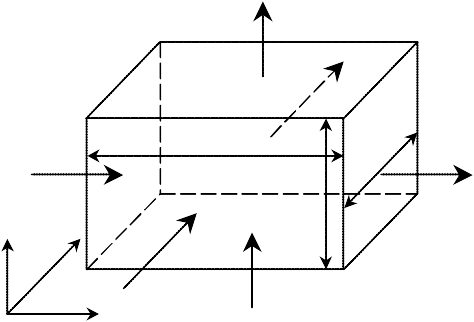 dx
dx
(vy)y+dy
dy
dz
(vx)x+dx
z0 w0
3.
z y
4. 0
x (vy)y (vz)z
1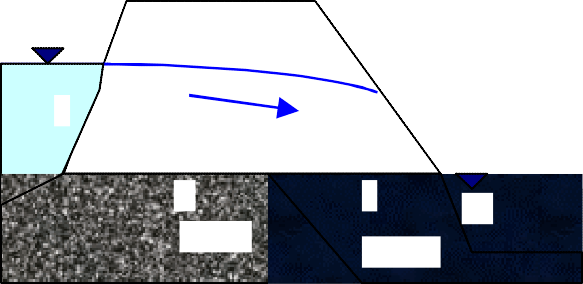
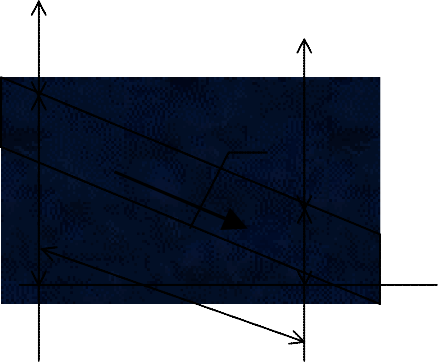
h 4 p /
1 K1 5
h
2 3 1
2
v
z1 z2
L
K3=0
5.
K2K1 1 2
6
![]() C
C
C(x,t–tф)
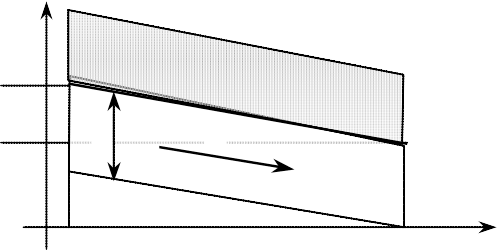 xф x
xф x
H1
m v
H2
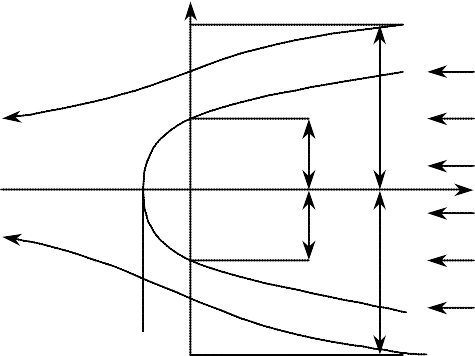
 y q
y q
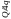 x0 x
x0 x
7. 1 2 x 8.
 9.
10.
11.
12.
9.
10.
11.
12.
![]()
а б

в г
1 2
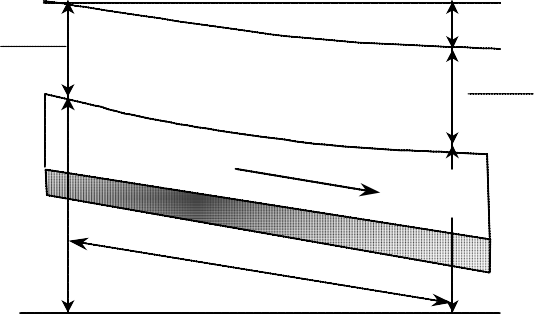 IG w
IG w
1
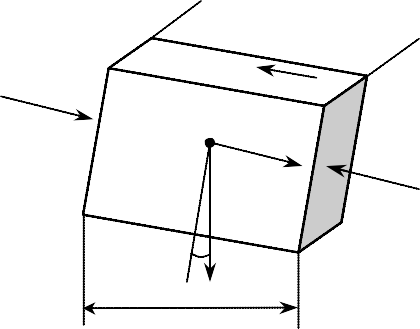 dFc 2
dFc 2
2v 2
2g
h
2v2
dP1
13.
I
z1
I0
l2–l1
2 2
2g
z2
14.
dFi dG
dx
dP2
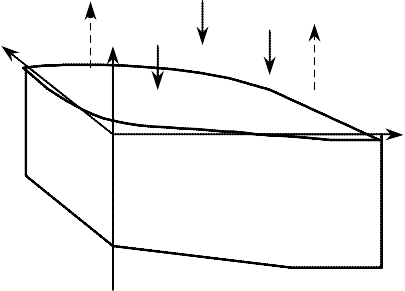 y I
y I
z
x
0 z=(x,y,t)
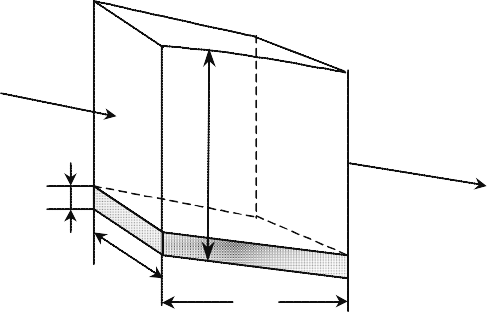 qs
qs
H
dzд
zп
q +q /xdx
s s
15.
z=–h(x,y)
16.
dy zд
dx
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
