1.4 Статистические графики

Для получения приблизительного представления о форме распределения строят графики распределения.

Полигон распределения - графическое изображение дискретного вариационного ряда распределения. По оси абсцисс откладывают варианты, а по оси ординат - частоты ряда. Полученные точки соединяются прямыми линиями.

Полученная таким образом линия называется эмпирической (фактической) кривой распределения. На нее оказывают влияние как общие (отражающие основную закономерность), так и случайные условия.

Если влияние случайных величин будет погашено, то будет установлена теоретическая кривая распределения. Она выражает определенный тип распределения, отвечает на вопрос о наличии определенного закона распределения. Познание законов распределения - наиболее важная цель статистического исследования. В каждом конкретном случае закономерность распределения может быть, а может и не быть.

Гистограмма распределения - графическое изображение интервального вариационного ряда распределения. Образуемые над интервалами столбики пропорциональны по высоте частотам значений признака по каждому интервалу. При неравных интервалах высота столбиков должна быть пропорциональна плотности распределения признака в соответствующем интервале.

Чтобы получить эмпирическую кривую, гистограмму нужно преобразовать в полигон. Для этого каждый интервал делим на две равные части (находим середину интервала), ставим точки и затем их соединяем последовательно отрезками прямых линий.

Эмпирическая кривая позволяет предварительно предположить форму теоретической кривой распределения, характеризующую функциональную связь между изменением варьирующего признака и изменением частот.

1.5 Асимметрия распределения и эксцесс

Асимметрия распределения означает, что частоты каких-либо двух вариантов, равноудаленных от центра распределения, не равны между собой. Графически асимметрия выражается различной длиной правой или левой ветви относительно максимальной ординаты. При асимметрии распределения значения средней арифметической, моды и медианы не совпадают.

Степень асимметрии определяется с помощью, например,

1. коэффициента асимметрии;

2. показателя асимметрии Пирсона.

Коэффициент асимметрии находится по формуле:

,

где - центральный момент третьего порядка, т.е.

.

Этот коэффициент характеризует асимметричность распределения крайних значений признака.

Показатель асимметрии Пирсона находится по формуле:

.

Показатель асимметрии Пирсона характеризует асимметричность распределения в средней части ряда.

Эксцесс характеризует степень островершинности эмпирической кривой относительно кривой нормального распределения.

Коэффициент эксцесса находится по формуле:

,

где - центральный момент четвертого порядка, т.е.

.

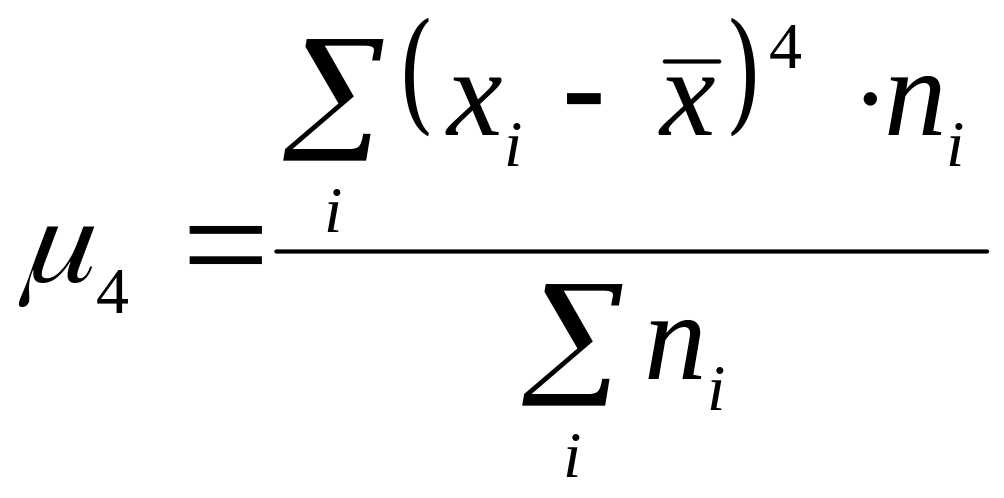Если получим , то вершины эмпирического и теоретического распределения совпадают. Если , то эмпирическая величина выше вершины соответствующего теоретического распределения, а если , то эмпирическая вершина ниже вершины соответствующего теоретического распределения.

Пример 1.4

Рассмотрим расчет показателей асимметрии и эксцесса по данным табл. 1.1. Воспользуемся найденным выше средним значением объема вы-

полненных строительных работ одним предприятием 670 млн. руб., средним квадратическим отклонением млн. руб., модальным значение объема выполненных строительных работ млн. руб.

Таблица 1.6

Группы предприятий		Расчетные показатели
по объему выполненных	Число	центральное
работ (закрытые	предприя-	значение
интервалы), млн. руб.	тий (n )	интервала
		( )
3	2	4	8	7
300-500	8	400	-157464000	42515280000
500-700	12	600	-4116000	288120000
700-1000	6	850	34992000	6298560000
1000-1300	4	1150	442368000	212336640000
Итого:	30	—	315780000	261438600000

Центральный момент третьего порядка:

.

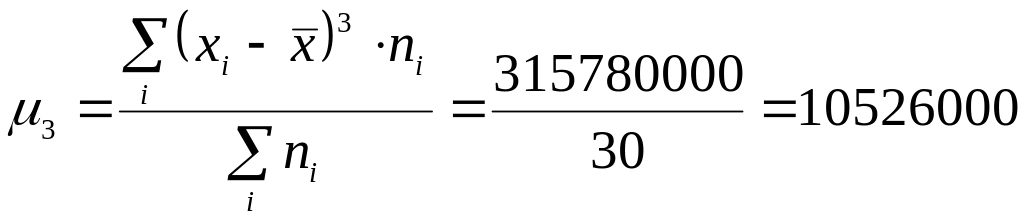Коэффициент асимметрии:

.

Показатель асимметрии Пирсона:

.

Таким образом, данное распределение имеет правостороннюю асимметрию, причем в крайних значениях признака асимметрия более значительная, чем в средней части распределения.

Центральный момент четвертого порядка:

.

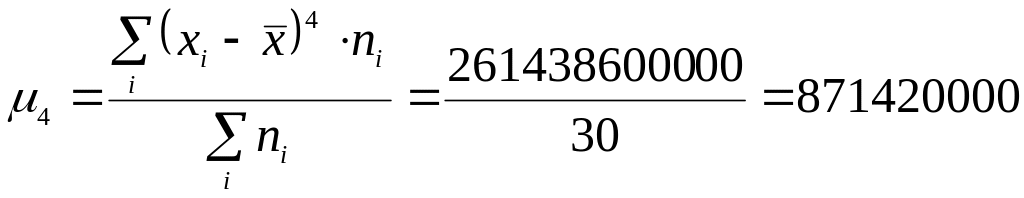Коэффициент эксцесса:

.

Таким образом, вершина данного распределения ниже вершины соответствующего теоретического нормального распределения.