5.2 Корреляционный метод анализа связей

Корреляционный метод имеет две основные задачи:

1) Обнаружить зависимость между факторным и результативным признаками и описать её форму с помощью уравнения регрессии;

2) Установить меру тесноты связи между признаками (в какой мере вариация х обуславливает вариацию у).

Приступая к изучению корреляционной зависимости, следует помнить о том что, прежде всего, необходимо провести предварительный теоретический анализ. Он должен ответить на вопрос о том, существует ли такая связь вообще. Из истории статистики известно, что несоблюдение этого правила не раз приводило исследователей к курьезным результатам.

Предварительный теоретический анализ позволяет во многих случаях подсказать и форму связи (прямолинейная или более сложная), установить, является ли связь прямой пли обратной.

Сказанное выше означает, что каждый, кто прибегает к использованию метода корреляции, должен хорошо владеть не только данным методом, но и знанием предмета своего исследования.

Корреляционную связь, в которой есть только один признак-фактор и один признак-результат, именуют парной. Уравнение, выражающее такую связь, представляют какой-либо математической формулой прямой или кривых линий (гипербола, парабола и др.).

Для нахождения формы связи и описания ее в виде уравнения линии используют:

— группировку статистических данных;

— построение графика эмпирической линии.

Если точек очень много, то рассматривают не линию, а облако точек на графике корреляционного поля. В реальной практике не всегда удается достаточно уверенно по эмпирической линии установить форму линии связи. В этих случаях принимают несколько вариантов формы связи, по каждому из них делают расчеты и в конце дают оценку вариантов с помощью показателя тесноты связи. Вариант, в котором теснота связи оказалась наиболее высокой, принимается за наиболее верный.

Если форма связи выражается прямой линией, то уравнение регрессии имеет вид:

,

где - теоретическое значение,

и - параметры уравнения.

Параметр экономической интерпретации не имеет. Параметр называется коэффициентом регрессии, который показывает насколько изменится

результативный признак ( ) при изменении признака-фактора (x) на одну единицу.

Параметры уравнения и находят из решения системы двух нормальных уравнений:

Решая эту систему относительно параметров a и b, получим:

,

.

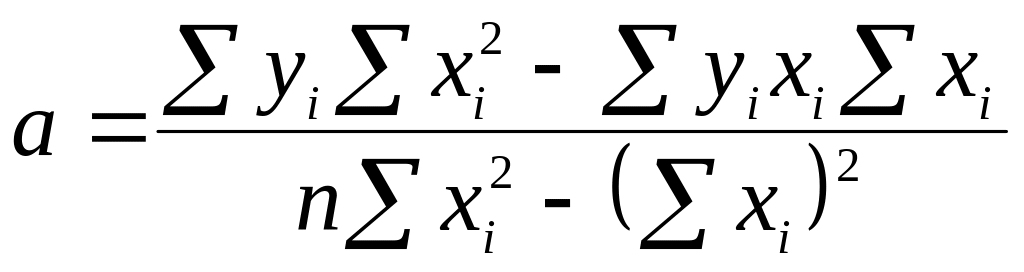Уравнение регрессии можно использовать для прогнозирования, если связь между факторным и результативным признаками достаточно тесная.

В случае прямолинейной формы связи теснота может быть измерена линейным коэффициентом корреляции по формуле:

.

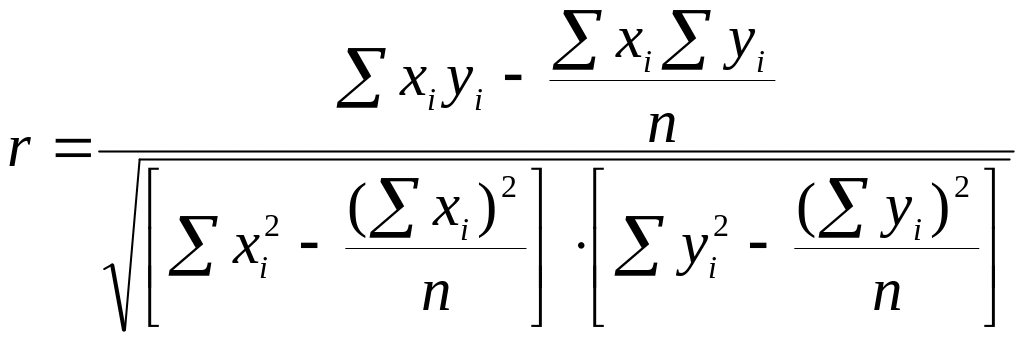Коэффициент корреляции может находится в пределах от 0 (связь отсутствует) до (связь полная). Знак «+» указывает на прямую, а знак «–» на обратную связь.

Существуют способы оценки тесноты связи. В частности, по таблице Чэддока тесноту связи определяют следующим образом (см. табл. 5.1):

Таблица 5.1

Значение коэффициента (по модулю)	Теснота связи
0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99	слабая умеренная заметная высокая весьма высокая

В упрощенном виде считают, что если коэффициент (по модулю) составляет от 0,1 до 0,3 – связь слабая, от 0,3 до 0,7 – средняя, от 0,7 и выше – тесная.

Пример 5.1

Имеются данные стоимости основных производственных фондов и объеме выпуска продукции по 10 предприятиям за отчетный год (см. табл. 5.2)

Таблица 5.2

Номер предприятия	Стоимость основных производственных фондов, млн. руб. (x)	Объем выпуска продукции, млн. руб. (y)
1 2 3 4 5 6 7 8 9 10	6 9 10 12 14 8 10 11 13 15	24 36 45 56 70 40 40 46 65 70

На основе приведенных данных:

1) для подтверждения положений логического анализа о наличии корреляционной прямолинейной зависимости между факторным признаком (стоимостью основных производственных фондов) и результативным признаком (объемом выпуска продукции) нанесите исходные данные на график корреляционного поля и сделайте выводы о форме связи, укажите ее формулу;

2) определите параметры уравнения связи и нанесите полученную при этом теоретическую линию на график корреляционного поля;

3) исчислите линейный коэффициент корреляции;

4) поясните значения показателей, полученных в пунктах 2) и 3);

5) используя полученную модель, сделайте прогноз о возможном объеме выпуска продукции на предприятии со стоимостью основных производственных фондов 7 млн. руб.

Решение

1. Величина основных производственных фондов определяет производственную мощность предприятия и поэтому логически можно считать, что зависимость между величиной основных производственных фондов и объемом выпуска продукции реально существует. Это подтверждается и показателями табл. 5.2. С увеличением основных производственных фондов отмечается рост объема выпуска продукции. В то же время в отдельных случаях наблюдается и другое — величина основных производственных фондов увеличивается, а увеличения объема выпуска продукции нет. Связь является корреляционной.

Для выяснения формы связи построим по данным табл. 5.2 график (см. рис. 5.1).

Рис. 5.1. Стоимость основных производственных фондов (x) и объем

выпуска продукции (y), млн. руб.

Эмпирическая ломаная линия на графике позволяет предположить, что связь выражается прямой линией, т.к. общей тенденцией на графике является направленность эмпирической линии из нижнего левого угла в верхний правый угол.

Итак, уравнение регрессии имеет вид:

,

2. Для нахождения параметров уравнения и составим табл. 5.3.

Таблица 5.3

	6 9 10 12 14 8 10 11 13 15	24 36 45 56 70 40 40 46 65 70	144 324 450 672 980 320 400 506 845 1050	36 81 100 144 196 64 100 121 169 225	576 1296 2025 3136 4900 1600 1600 2116 4225 4900
Итого:	108	492	5691	1236	26374

Так как в нашем случае n=10, то

;

.

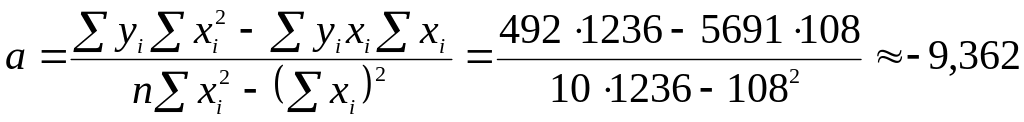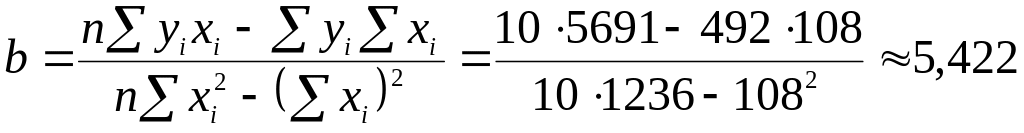Итак, уравнение регрессии в нашем случае будет иметь вид:

.

Изобразим полученную теоретическую линию на график корреляционного поля (см. рис. 5.1).

Полученное уравнение позволяет оценить по предприятиям, как они использовали возможности для производства продукции, заложенные в величине основных производственных фондов.

Так, по первому предприятию при :

; т.е. фактический объем выпуска продукции выше теоретической величины на 0,83 млн.руб.

По последнему предприятию при :

; т.е. возможности производства недоиспользованы на 1,968 млн. руб.

3. Найдем значение линейного коэффициента корреляции

.

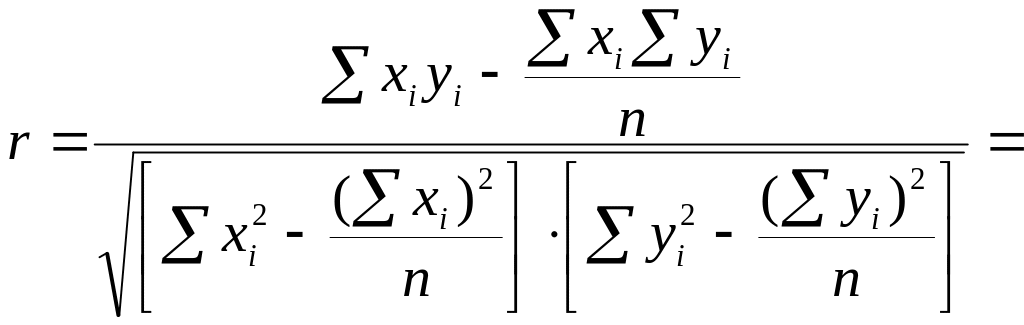
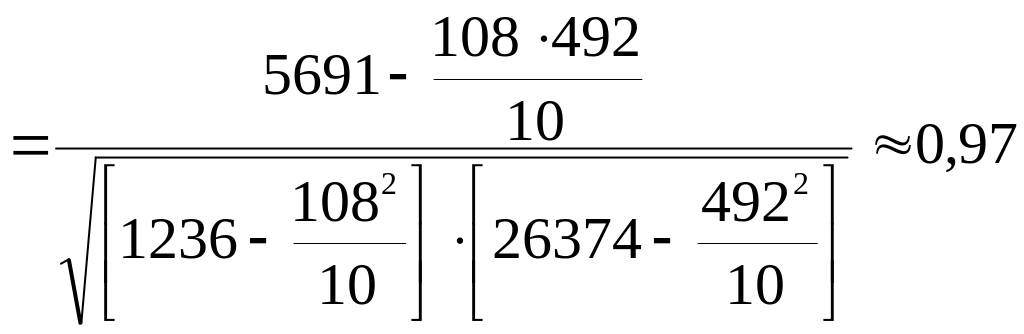4. Параметр =5,422 означает, что увеличение стоимости основных производственных фондов на 1 млн. руб. ведет к росту объема выпуска продукции на 5,422 млн. руб.

Значение линейного коэффициента корреляции r=0,97 свидетельствует о наличии весьма высокой связи между величиной стоимости основных производственных фондов и объемом выпуска продукции. Следовательно, полученное уравнение регрессии может быть использовано для прогнозирования.

5. Прогнозируемая величина объема выпуска продукции на предприятии со стоимостью основных производственных фондов 7 млн. руб. будет:

(млн. руб.).