4.4 Средние индексы

Агрегатный индекс может быть преобразован в средний арифметический или средний гармонический. Эти формулы используют тогда, когда информация не позволяет сделать расчет по формуле агрегатного индекса, но достаточна для расчета индексов по преобразованным формулам.

Так, например, агрегатный индекс физического объема товарооборота

может быть преобразован в средний арифметический, если выразить из индивидуального индекса физического объема: , т.е. и подставить в выше приведенную формулу. Итак,

.

Пример 4.2

Имеются данные о производстве продукции заводом за два года (см. табл. 4.2):

Таблица 4.2

Наименование продукции	Стоимость произведенной продукции в базисном году, тыс. руб. ( )	Изменение количества произведенной продукции в отчетном году, %.
Станки модели «А» Станки модели «Б» Посуда	25000 10000 5000	-35,0 +20,0 +52,0

Требуется вычислить агрегатный индекс физического объема производства продукции.

Решение

Для расчета агрегатного индекса физического объема производства продукции воспользуемся формулой среднего арифметического индекса.

Индивидуальные индексы физического объема составляют:

станки модели «А» — 100% – 35% = 65% или 0,65;

станки модели «Б» — 100% + 20% = 120% или 1,20;

посуда — 100% + 52% = 152% или 1,52.

Итак, агрегатный индекс физического объема производства продукции:

или 89,6%. Следовательно, физический объем производства продукции за указанный период сократился на 10,4%.

Аналогично, агрегатный индекс цен

может быть преобразован в средний гармонический, если выразить из индивидуального индекса цен: , т.е. и подставить в выше приведенную формулу.

Итак,

.

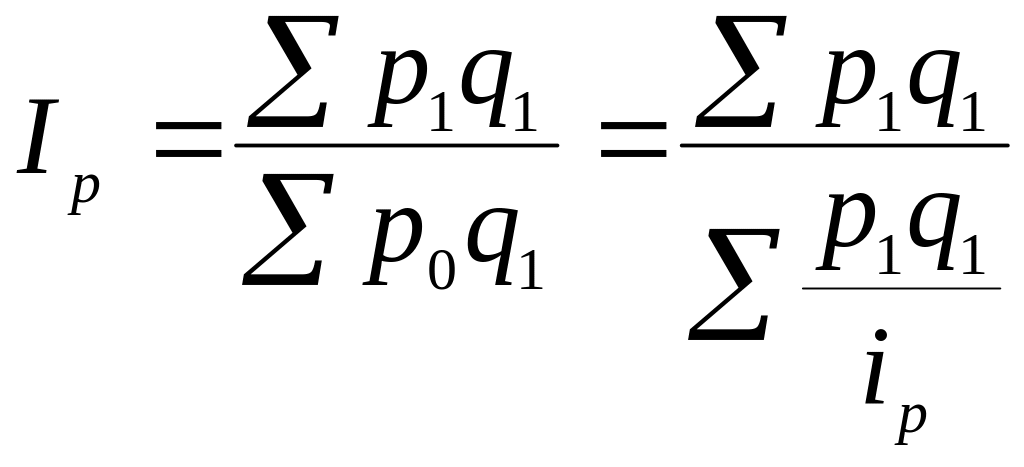Пример 4.3

По приведенным данным (см. табл. 4.3) вычислить агрегатный индекс цен.

Таблица 4.3

Наименование товаров	Товарооборот за 1995 год в фактических ценах, тыс. руб. ( )	Изменение цен в 1995 г. по сравнению с 1994 г. в процентах
Мясо Молоко Сахар Картофель	810 1260 930 500	+30 +24 +42 –5

Решение

Для расчета агрегатного индекса цен воспользуемся формулой среднего гармонического индекса.

Индивидуальные индексы цен составляют:

Мясо — 100% + 30% = 130% или 1,30;

Молоко — 100% + 24% = 124% или 1,24;

Сахар — 100% + 42% = 142% или 1,42;

Картофель — 100% – 5% = 95% или 0,95.

Итак, агрегатный индекс цен:

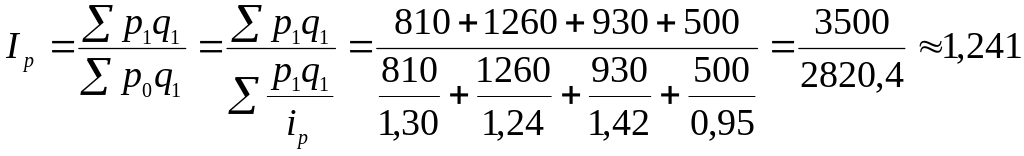
или 124,1%. Следовательно, цены на товары в 1995 году увеличились по сравнению с 1994 годом на 24,1%

5. Корреляционно-регрессионный анализ

5.1 Виды взаимосвязей, изучаемые статистикой

Изучение взаимосвязей в обществе и природе – важнейшая познавательная задача статистики.

Существуют различные виды и формы связей. По харак­теру зависимости явлений различают:

— функциональную (полную) связь;

— корреляционную (неполную) связь.

Функциональные связи характеризуются однозначным изменением результативного признака под влиянием изменения факторного признака. Так, например, функциональная связь существует между площадью и радиусом круга. Функциональная связь выражается формулой у=f(х).

Корреляционная связь проявляется лишь в среднем, в массе случаев. При корреляционной зависимости тот или иной признак изменяется (варьирует) под влиянием действия целого комплекса факторов, часть которых имеет основное значение для совокупности, а другая — второстепенное, хотя, может быть, и сильно влияет на отдельные единицы совокупности. Так, например, уровень производительности труда рабочих зависит от энерговооруженности и фондовооруженности труда. В то же время уровень производительности труда в какой-то мере зависит от многих других факторов, в том числе и от особенностей условий работы каждого предприятия. Для обнаружения корреляционной зависимости нужно взять не один и не два случая, а большое их число. Только в массе случаев индивидуальные особенности и второстепенные факторы сгладятся и зависимость, если она имеет существенную силу, проявится достаточно отчетливо.

Корреляционную связь можно выразить формулой: у=f(х)+ . Здесь результативный признак у зависит от признака-фактора х, но имеется еще и остаточное влияние второстепенных причин, выраженное величиной — .

По направлению действия факторного признака различают связи:

— прямые (увеличение факторного признака вызывает увеличение результативного признака, так же и уменьшений одного ведет к уменьшению другого признака);

— обратные (увеличение факторного признака ведет и уменьшению признака результативного и наоборот).

Связи между явлениями могут быть:

— сильными (тесными);

— слабыми.

Статистические методы позволяют измерять силу взаимосвязей. По аналитическому выражению связи могут быть линейные и нелинейные.

Корреляционная связь может быть:

— парной (связь двух признаков);

— многофакторной (множественной), когда на результативный признак одновременно оказывают влияние несколько признаков факторов.