4. Виконання похилих перерізів

4.1. Виконання похилого перерізу фронтально-проекціюючою площиною

На рис. 4.1 наведено приклад виконання фронтального похилого перерізу А–А.

Рис. 4.1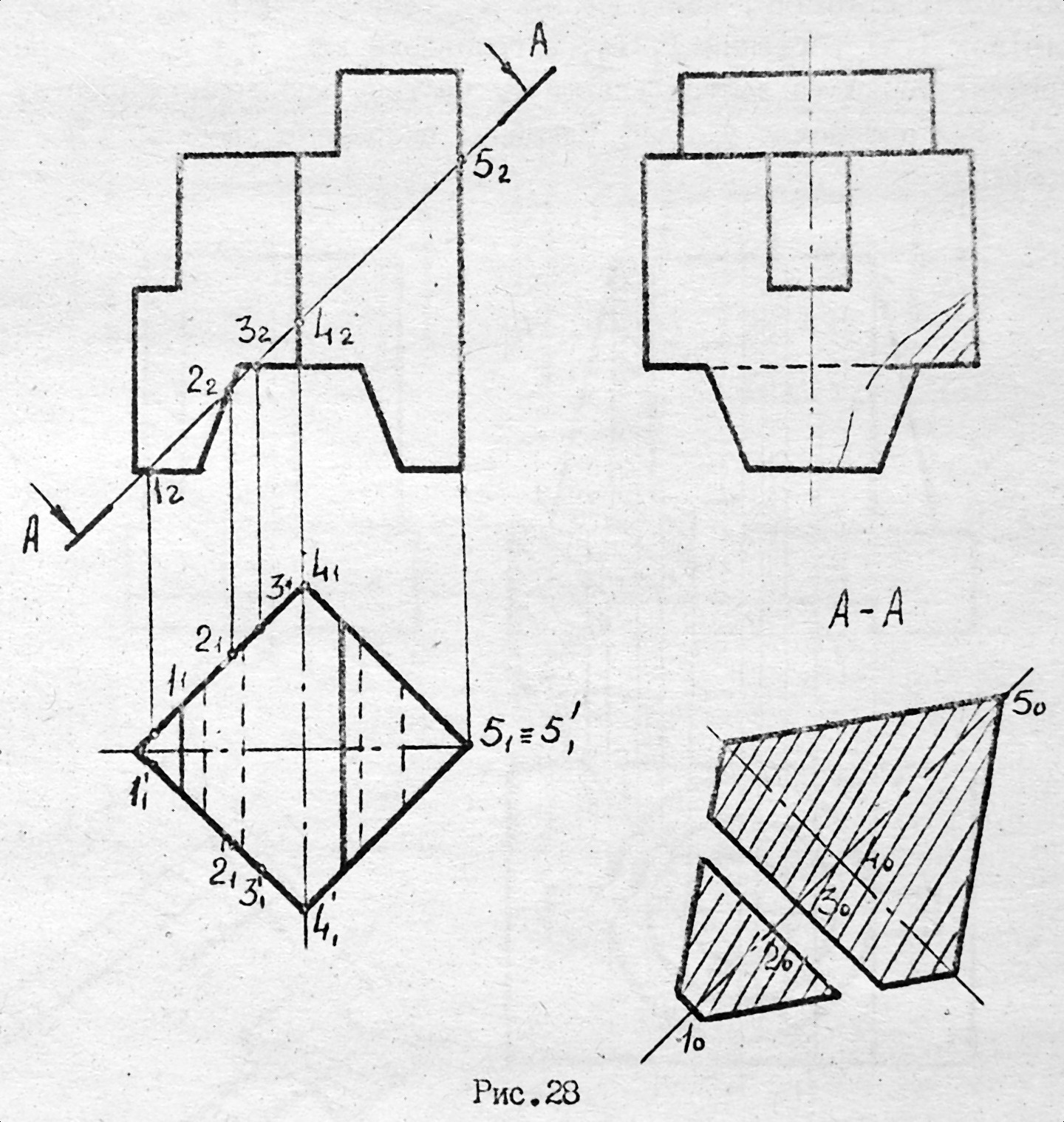

На сліді січної площини А–А відмічають точки перетину сліду січної площини з лініями видимого та невидимого контурів деталі (опорні та проміжні точки) від 1₂ до 5₂.

На вільному полі креслення проводимо пряму 1₂…5₂ , паралельну сліду січної площини А–А, на якій відкладаються натуральні величини відстаней між точками 1₂–2₂; 2₂–3₂ та ін. Через те що площина А–А перпендикулярна П₂, натуральні розміри перерізу в точках 1, 2, 3, 4, 5 у напрямку, перпендикулярному до П₂, будуть проекціюватися в натуральну величину.

23

Якщо січна площина проходить через вісь круглих отворів та заглиблень (циліндричних, конічних, сферичних), то контур такого заглиблення чи отвору показують повністю, тобто січення виконують як розріз. Якщо січна площина проходить через некруглий отвір, його зображення виконують за принципом перерізу (див. рис. 3.13).

3.4. Штрихування в розрізах та перерізах

Перерізи і розрізи виділяють на кресленнях та перерізах штрихуванням, яке виконують за ГОСТ 2.306-68 в залежності від матеріалу деталі.

Лінії штрихування виконують під кутом 45° до рамки креслення. Якщо напрямок штрихування збігається з напрямком ліній контуру, дозволяється виконувати штрихування під кутом 30° та 60°. Лінії штрихування дозволяється наносити з нахилом вправо чи вліво, не обов’язково в один бік для всіх розрізів і перерізів однієї і тієї ж деталі

Відстань між лініями штрихування повинна бути від 1 до 10 мм у за­лежності від матеріалу та площини штрихування. Для металу рекомендується 2...4 мм.

Довгі та вузькі площини, ширина яких на кресленні не перевищує 2...4 мм, рекомендується штрихувати від руки не повністю, а в окремих місцях. Вузькі площини (до 2 мм) дозволяється затушовувати, залишивши просвіт між сусідніми деталями (рис. 3.18).

Рис. 3.18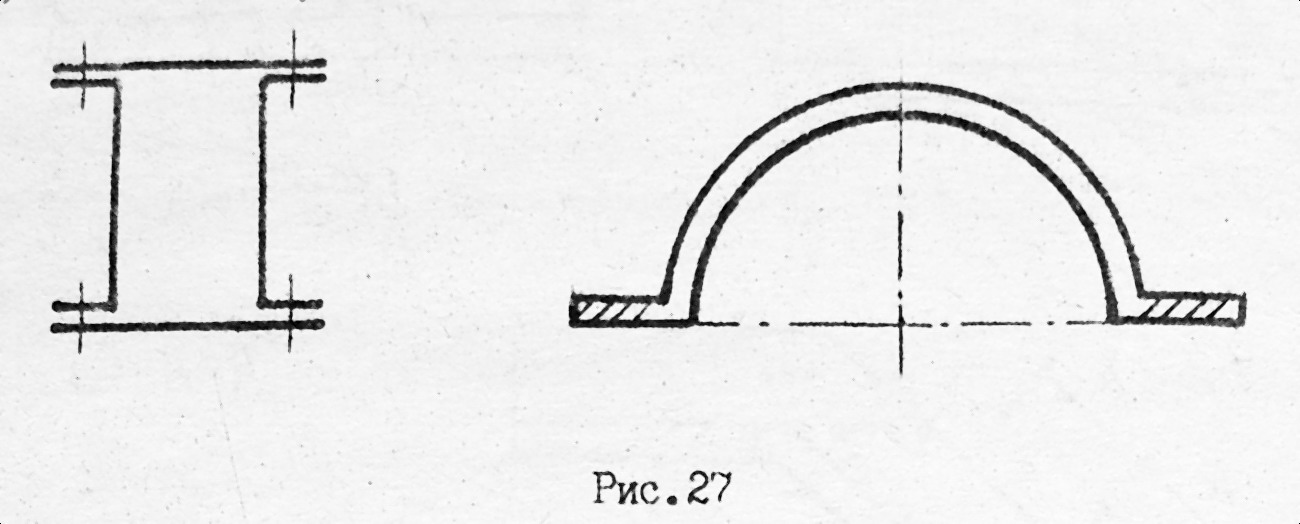

22

На площині П₁ видимою є тільки верхня основа призми; на П₂ – грані АЕГВ та ВГДС, на П₃ видимою буде тільки грань АЕГВ.

Визначення проекцій точок, що лежать на поверхні призми, виконується за належністю цих точок граням і відповідно до належності проекцій точок проекціям граней. На рис. 2.2 наведено находження горизонтальної та профільної проекцій точки (М₁ та М₃) за заданою М₂.

2.3. Піраміда

Пірамідою називається багатогранник, одна грань якого (основа) – багатокутник, а бокові грані – трикутники з загальною точкою – вершиною піраміди (рис. 2.3).

Рис. 2.3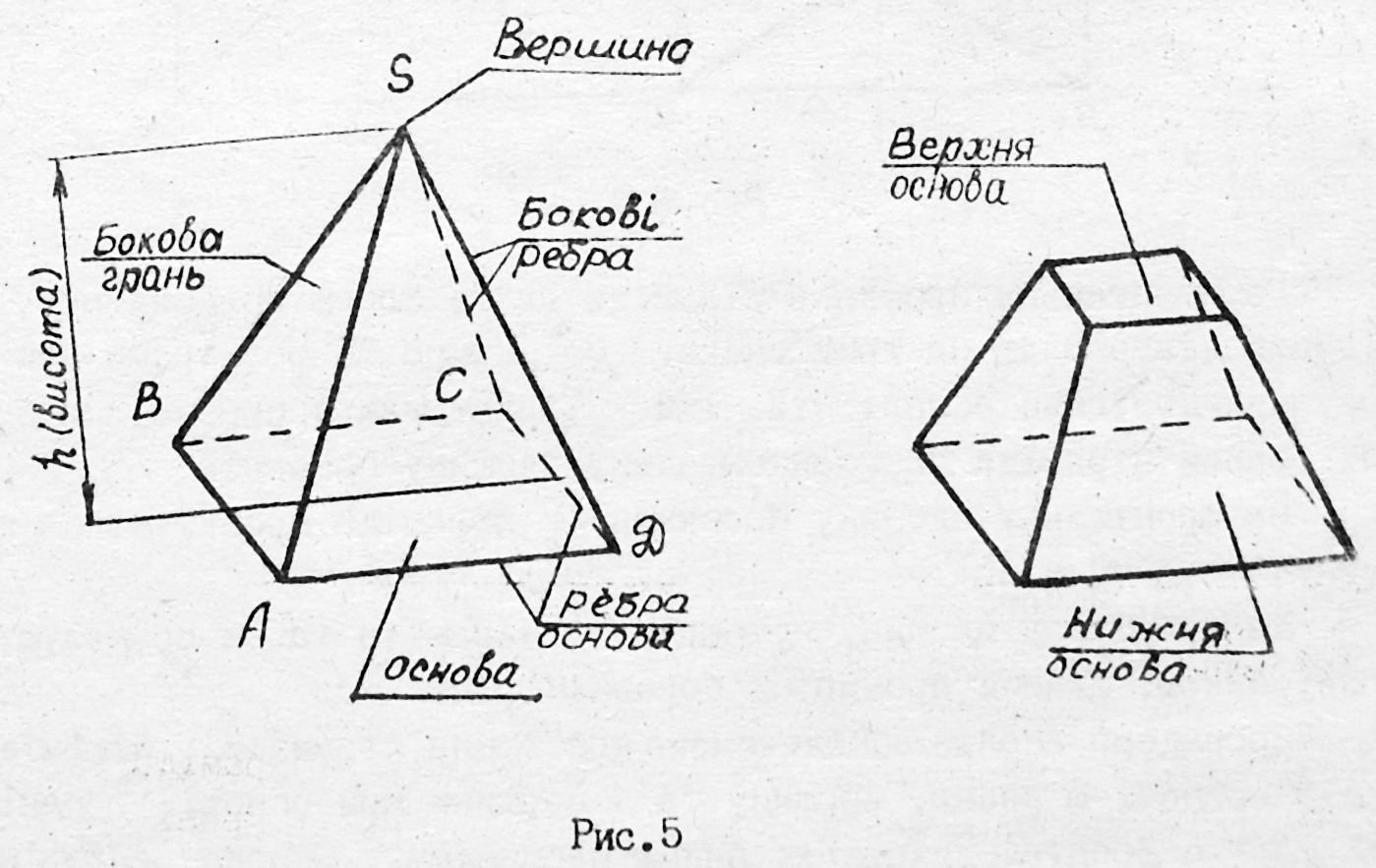

Ребра піраміди поділяються на бокові та ребра основи. За формою основи піраміди бувають трикутні, чотирикутні, п’ятикутні та ін.

Піраміда називається правильною, якщо її основою є багатокутник і вісь проходить через центр основи. Якщо вершина піраміди разом з частиною бокових граней відсічена, то така піраміда називається зрізаною.

На рис. 2.4 показане комплексне креслення чотирикутної піраміди.

7

Рис. 2.4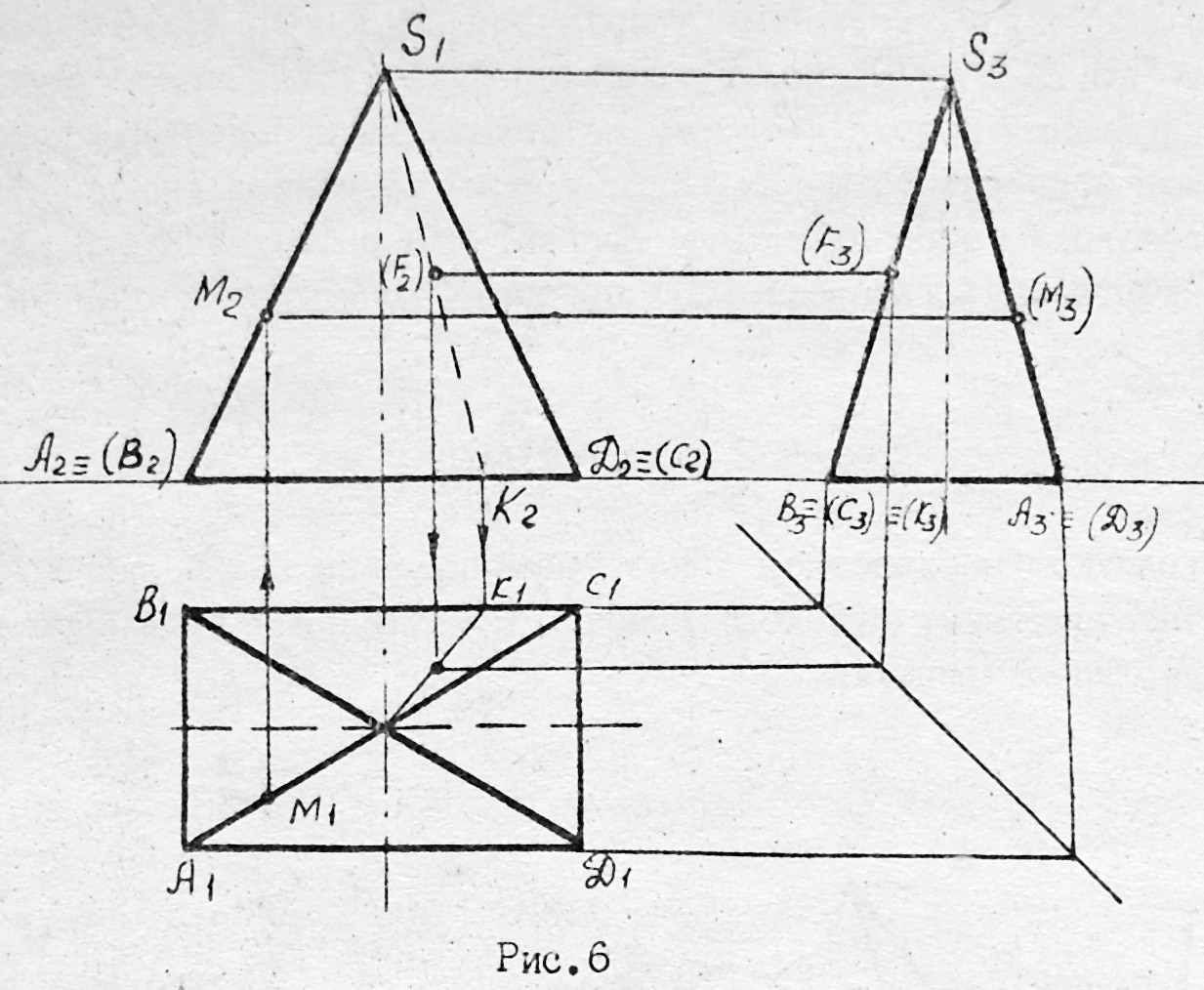

Горизонтальна проекція піраміди являє собою прямокутник, поділений діагоналлю на трикутники. За формою та розмірами цей прямокутник дорівнює основі піраміди. Трикутники є проекціями бокових граней піраміди на горизонтальну площину проекцій П₁.

На фронтальну площину проекцій П₂ піраміда проекціюється трикутником, який є проекцією бокової грані АSД. На профільну площину проекцій П₃ піраміда також проектується трикутником, який є проекцією бокової грані ВSА.

Виконаємо аналіз комплексного креслення піраміди. Піраміда має 5 граней, 8 ребер, вершину та 4 вершини при основі. Грані BSA та ДSС є фронтально-проекціюючими площинами. Основа АВСД на П₁ проектується у натуральну величину.

На фронтальній площині проекцій П₂ видимою є тільки грань АSД, а на П₃ – грань ВSА. На горизонтальній площині проекцій видимими є всі 4 бокові грані, а основа – невидима.

8

Рис. 3.13

Рис. 3.14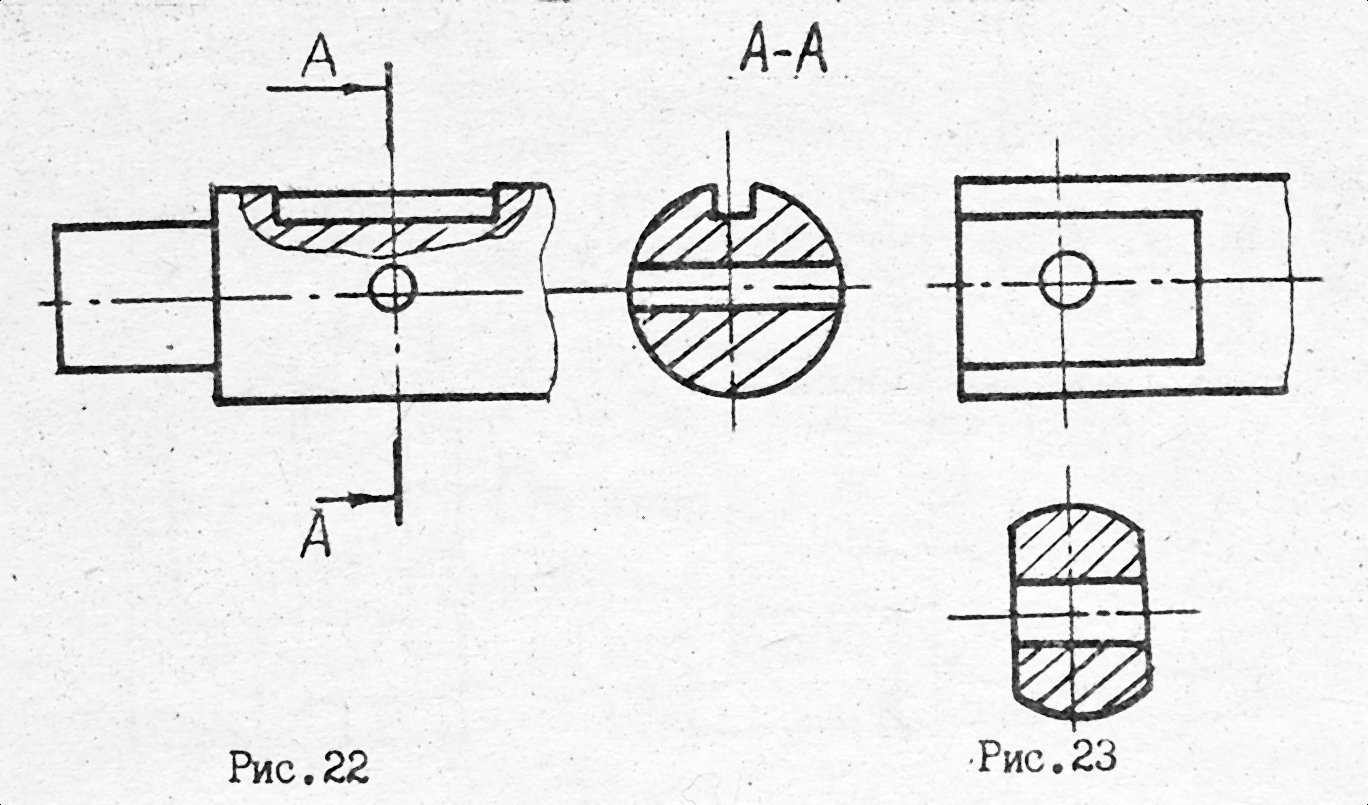

Винесені перерізи за своєю побудовою та розташуванням повинні відповідати напрямку, вказаному стрілками. Дозволяється розташовувати перерізи на будь-якому місці креслення з поворотом зображення. У цих випадках до напису додають слово «повернуто» (рис. 3.17). Напрямок січної площини Повинен бути таким, щоб одержувати тільки нормальні поперечні перерізи. Для кількох однакових перерізів, які належать одному предмету, лінії перерізів позначають однією літерою і креслять лише один переріз (рис. 3.17).

Рис. 3.15

Рис. 3.16

Рис. 3.17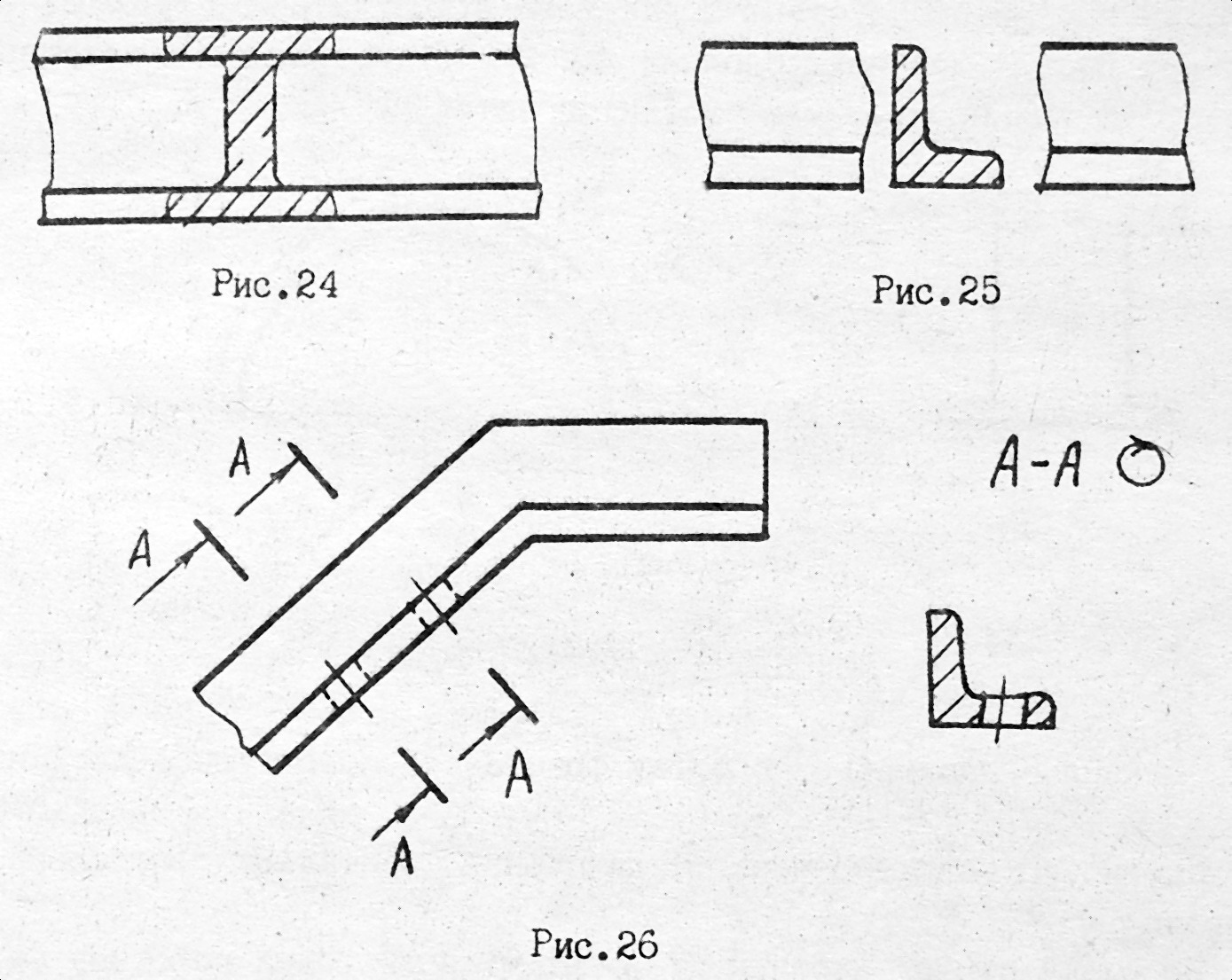

21

Подільною лінією виступає вісь симетрії фігури (рис. 3.12).

Рис. 3.12

Перерізом називають зображення, утворене при перетині в думці предмета однією чи кількома площинами.

У перерізі показують тільки те, що виходить у січній площині. Переріз, як і розріз, – зображення умовне. Умовність його полягає в тому, що фігура, утворена в перерізі, окремо від предмета не існує, її У думці відривають та зображають на вільному полі креслення.

Перерізи поділяють на винесені та накладені.

Переріз називають винесеним, якщо він виконаний окремо від основного зображення; його зображують такими ж позначеннями, як і розрізи (рис. 3.13).

Переріз, виконаний на продовженні сліду січної площини, не позначають літерами – та стрілками (рис. 3.14).

Переріз називають накладеним, якщо він розташований на зображенні предмета. Накладені перерізи обводять тонкою суцільною лінією та штрихують під кутом 45° до основного напису креслення (рис. 3.15).

Переріз дозволяється виконувати у розриві креслення предмета, якщо його профіль однорідний (рис. 3.16).

20

При визначенні проекцій точок, які лежать на елементах піраміди, користуються правилами нарисної геометрії. Якщо точка лежить на грані, то її проекції будуть лежати на проекціях прямої, проведеної через цю точку.

Приклад 1. На рис. 2.4 задана проекція точки М (М₁), яка лежить на проекції ребра піраміди А₁S₁. Треба знайти проекції точки М₂ та М₃.

Рішення: якщо М₁ лежить на А₁S₁, то М₂ буде лежати на А₂S₂, а М₃ – на А₃S₃. Проводимо вертикальну та горизонтальну лінії зв’язку до перетину відповідно до А₂S₂ та А₃S₃ і знаходимо проекції М₂ і М₃.

Приклад 2. Задана точка Р проекцією Р₂, що лежить на грані ВSС, яка на площині проекцій П₂ є невидимою. Знайти проекції Р₁ та Р₃.

Рішення: у грані піраміди ВSС потрібно через вершину та точку Р провести пряму лінію. На фронтальній площині проекцій її проекція буде S₂ К₂. Знаходимо проекцію прямої SK на П₁. Причому точка К₁ лежить на прямій В₁С₁. Проводимо з точки Р₂ вертикальну лінію зв’язку до перетину з S₁К₁, одержимо точку Р₁, знаходимо проекцію прямої SК на П₃. S₃К₃≡S₃В₃≡S₃С₃. Провівши горизонтальну лінію зв’язку точки F₂ до перетину з прямою S₃K₃ одержуємо F₃.

2.4. Циліндр

Циліндром називається тіло, обмежене циліндричною поверхнею та двома паралельними площинами (основами).

Циліндр називається прямим, якщо його твірні перпендикулярні до основи. Технічні деталі найчастіше мають форму прямих кругових циліндрів.

Комплексне креслення прямого кругового циліндра показано на рис. 2.5. Горизонтальна проекція циліндра являє собою коло, дві інші проекції – прямокутники, висота їх дорівнює висоті циліндра, а ширина – діаметру основи.

На горизонтальній площині проекцій видимою буде тільки верхня основа; на фронтальній – тільки передня частина циліндричної поверхні; на профільній – тільки ліва частина циліндра. Проекція нарисних твірних А₂В₂ та С₂Д₂ відділяє видиму та невидиму частини циліндра на П₃.

9

Рис. 2.7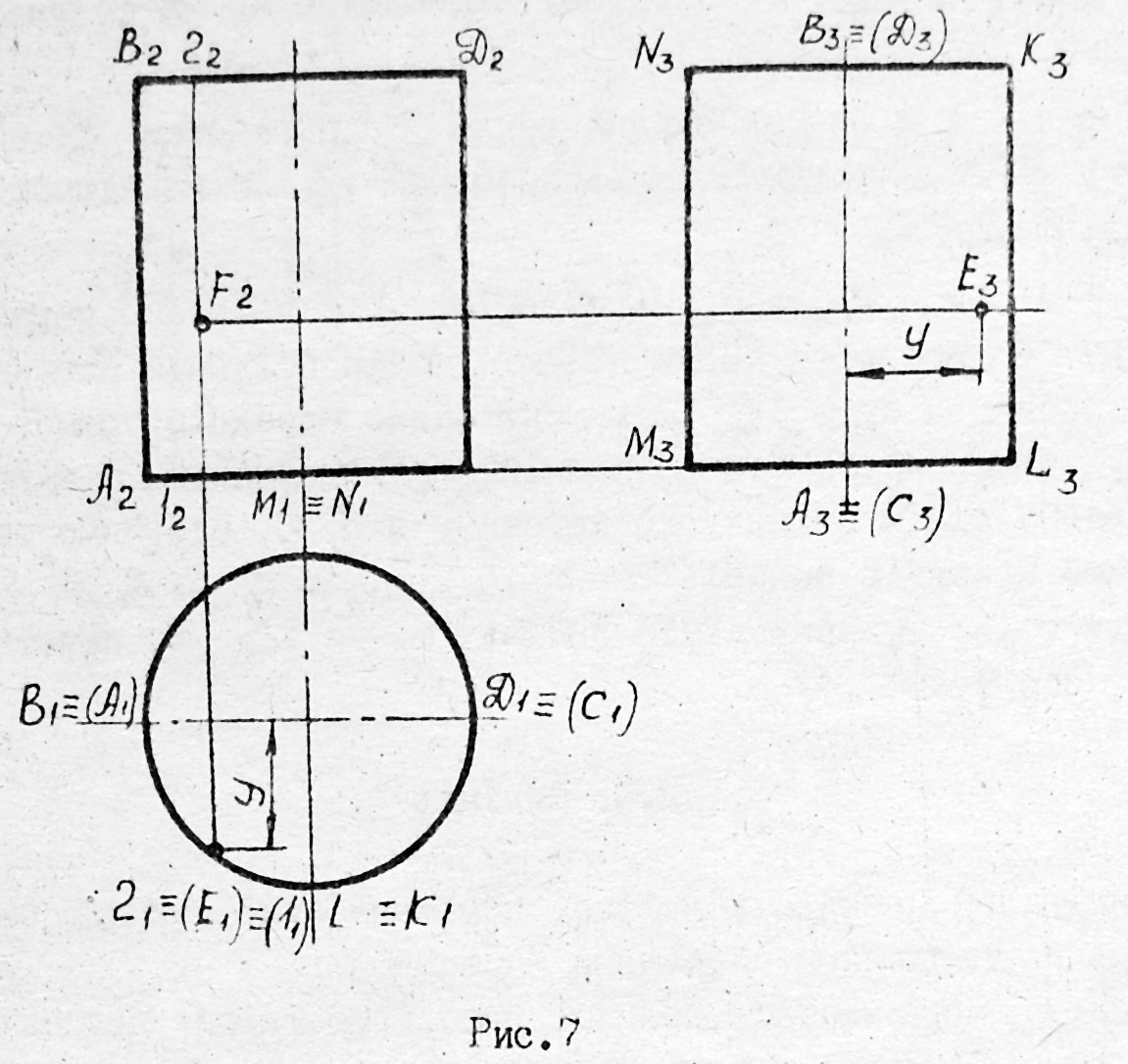

Визначення проекцій заданих точок здійснюється за допомогою твірних, на яких лежать ці точки. Потім з допомогою ліній зв’язку знаходять проекції заданих точок.

Нехай задана проекція точки Е(Е₂). Визначити проекції цієї точки Е₁ та Е₃. На П₁ задана точка проектується на коло. Проводимо з точки Е₂ горизонтальну лінію зв’язку. На П₃ по цій лінії від осі вправо відкладаємо координату Y, яку взято з П₁. Одержимо точку Е₃ координатним методом.