Теория вероятностей.

Тема 1: случайные события.

Общие указания.

1. Решение задач этой темы основано на простейшей модели теории вероятностей для вычисления вероятностей. Данную модель называют «классической схемой»,а определение вероятности – формулой классической вероятности. В этой модели основным понятием является понятие элементарный исход (элементарное событие).

Например, в задаче 1.1 элементарный исход – извлеченная перчатка – черная (или бежевого цвета). Для вычисления вероятности по классической формуле применяют следующий алгоритм:

1. Уяснить, в чем состоит эксперимент.

2. Установить, являются ли исходы равновозможными и несовместными.

3. Сформулировать событие, вероятность наступления которого необходимо найти (например, А – извлечена черная пара перчаток).

4. Определить пространство элементарных исходов и число его элементов - .

5. Подсчитать число исходов, благоприятствующих событию – N(А) (для события А).

6. Найти вероятность события А (или В, С,…), согласно формуле классического определения вероятности:

P(A)=

2. Кроме классического определения вероятности, при решении задач применяются основные формулы теории вероятностей теоремы сложения и умножения. Следует помнить, что при использовании формул сложения вероятностей нужно проверять несовместность (или совместность) событий, а при использовании формул умножения – независимость (или зависимость) событий. С этим связан правильный выбор формул, так как вычисление вероятностей искомых событий основано на составлении формул, выражающие эти события через элементарные события с помощью операций сложения, умножения и отрицания (противоположных событий), а затем применяются основные формулы.

Задача 1.1

В ящике находятся 6 одинаковых пар перчаток черного цвета и 5 одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.

Решение:

Пусть А – случайное событие, что извлечена черная пара перчаток – левая и правая; В – извлечена бежевая пара (левая и правая). Тогда событие С=А+В – извлеченные из ящика две перчатки одного цвета и образуют пару. А и В – несовместные события. Р(С)=Р(А)+Р(В) – формула сложения для несовместных событий. Вероятности Р(А) и Р(В) вычислим по формуле классического определения вероятности:

1) 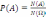, где - число всех исходов (сколькими способами можно извлечь две перчатки из всего количества перчаток). - число благоприятных исходов (сколькими способами можно извлечь из черных перчаток две, образующих пару). Для подсчета и применяются формулы комбинаторики. В данном случае – сочетание

По условию задачи, в ящике 6 пар черных перчаток и 5 пар бежевых. Значит, всего перчаток l=(6+5)*2=22. Отсюда, – всего способов извлечь 2 перчатки из 22.

Найдем N(A). Так как левых 6 перчаток и правых 6, то по принципу умножения из комбинаторики 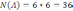. По классическому определению:

2) , где – тоже, что и для события A

(Пять способов выбрать левую бежевую и пять способов выбрать правую бежевую и по принципу умножения способов выбора левой и правой перчаток).

Тогда Р(С)=Р(А)+Р(В)=0,156+0,108=0,264

Тренинг умений: [2] №№1,11,17,39,41

Задача 1.2

В урне находится 3 шара белого цвета и 4 шара черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется:

а) Ровно два белых шара;

б) Не менее двух белых шаров.

Решение:

Эту задачу можно решить двумя способами: