Исходные данные
№ п/п |
Стоимость имущества банка, млн. руб. |
Прибыль банка, млрд.руб. |
1 |
9760 |
329 |
2 |
9840 |
169 |
3 |
9590 |
186 |
4 |
10500 |
225 |
5 |
9320 |
212 |
6 |
10070 |
199 |
7 |
7760 |
103 |
8 |
7950 |
97 |
9 |
8210 |
140 |
10 |
8060 |
156 |
11 |
7860 |
113 |
12 |
9780 |
186 |
13 |
8000 |
159 |
14 |
9500 |
163 |
15 |
9200 |
155 |
16 |
7940 |
115 |
17 |
10150 |
221 |
18 |
7500 |
103 |
19 |
8470 |
127 |
20 |
9010 |
147 |
21 |
7850 |
123 |
22 |
10300 |
135 |
23 |
10250 |
165 |
24 |
9480 |
155 |
25 |
7700 |
109 |
26 |
7820 |
107 |
27 |
8590 |
127 |
28 |
8040 |
156 |
29 |
9240 |
150 |
30 |
7650 |
105 |
Построим линию регрессии
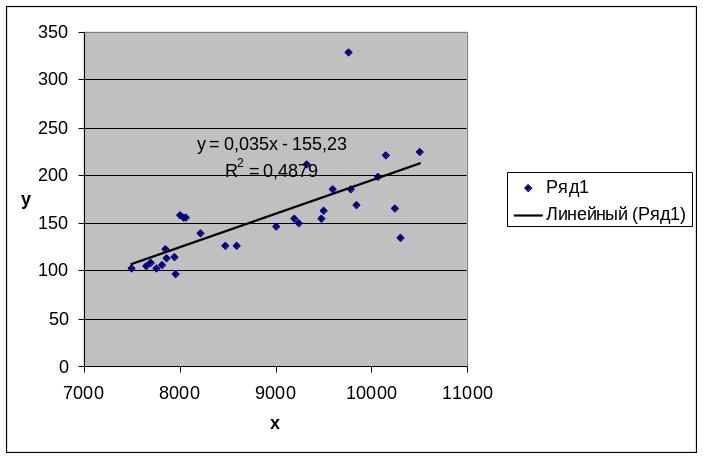
Видим, что с увеличением стоимости имущества прибыль банка увеличивается, следовательно связь прямая.
Линейный коэффициент корреляции определяется по формуле:
,
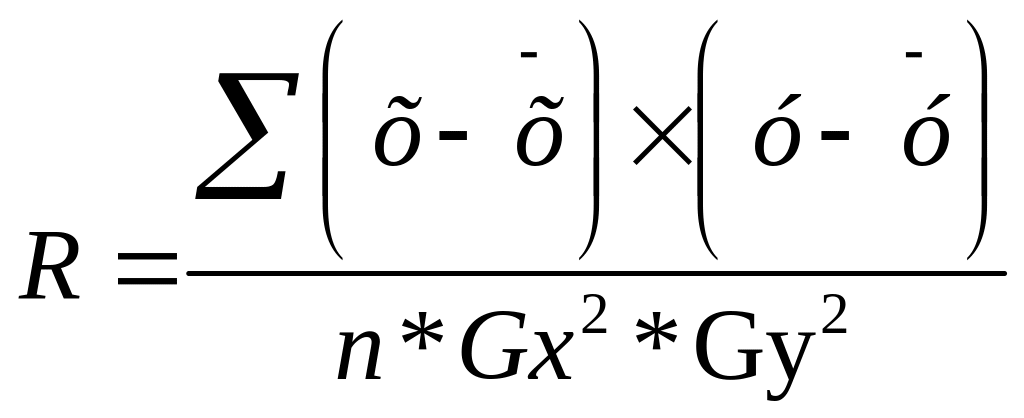где х – факторный признак, у - результативный
признак, Gх
– средний квадрат отклонений по признаку
Хi,
Gу
–средний квадрат отклонений по признаку
Уi.
Gx2
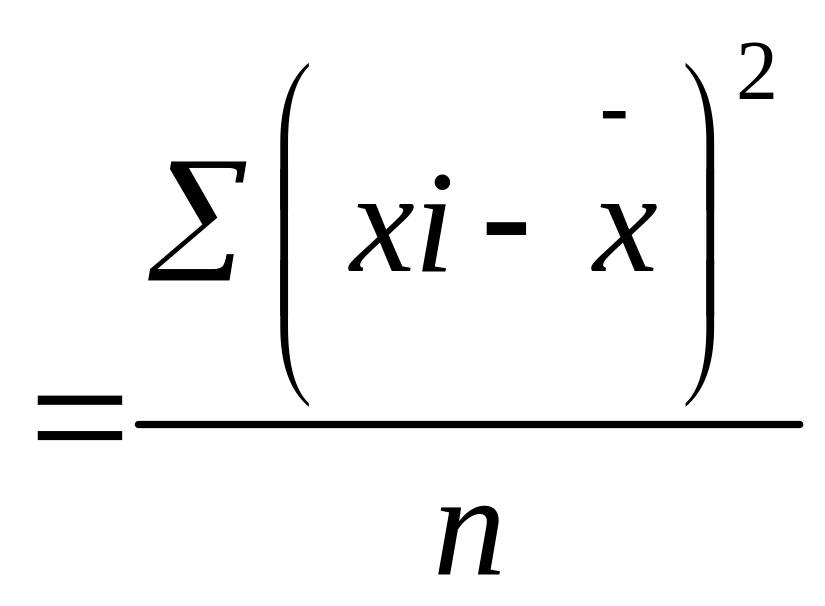
Gy2
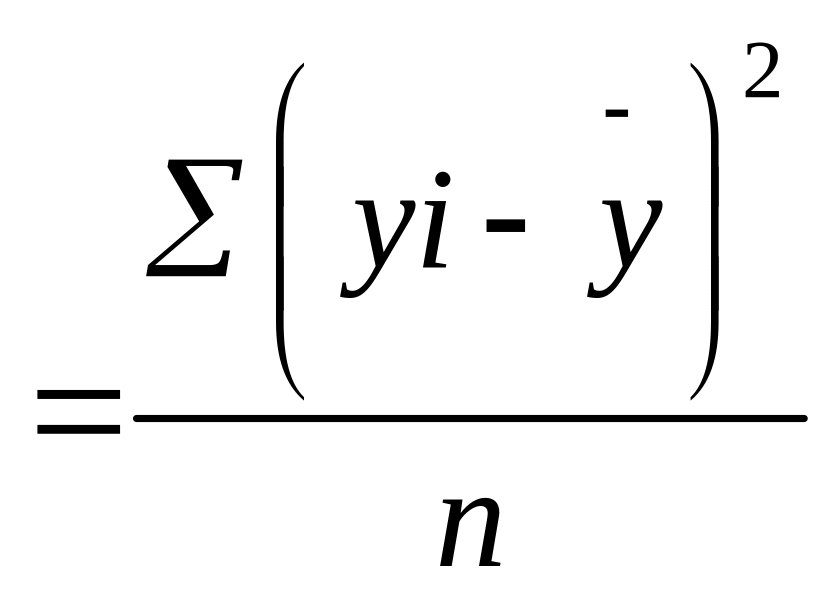
Для удобства расчетов используем вспомогательную таблицу:
Таблица 3.1
Исходные данные
№ п/п |
x |
y |
|
|
|
|
|
1 |
9760 |
329 |
913,667 |
174,433 |
834786,778 |
30426,988 |
159373,922 |
2 |
9840 |
169 |
993,667 |
14,433 |
987373,444 |
208,321 |
14341,922 |
3 |
9590 |
186 |
743,667 |
31,433 |
553040,111 |
988,054 |
23375,922 |
4 |
10500 |
225 |
1653,667 |
70,433 |
2734613,444 |
4960,854 |
116473,256 |
5 |
9320 |
212 |
473,667 |
57,433 |
224360,111 |
3298,588 |
27204,256 |
6 |
10070 |
199 |
1223,667 |
44,433 |
1497360,111 |
1974,321 |
54371,589 |
7 |
7760 |
103 |
-1086,333 |
-51,567 |
1180120,111 |
2659,121 |
56018,589 |
8 |
7950 |
97 |
-896,333 |
-57,567 |
803413,444 |
3313,921 |
51598,922 |
9 |
8210 |
140 |
-636,333 |
-14,567 |
404920,111 |
212,188 |
9269,256 |
10 |
8060 |
156 |
-786,333 |
1,433 |
618320,111 |
2,054 |
-1127,078 |
11 |
7860 |
113 |
-986,333 |
-41,567 |
972853,444 |
1727,788 |
40998,589 |
12 |
9780 |
186 |
933,667 |
31,433 |
871733,444 |
988,054 |
29348,256 |
13 |
8000 |
159 |
-846,333 |
4,433 |
716280,111 |
19,654 |
-3752,078 |
14 |
9500 |
163 |
653,667 |
8,433 |
427280,111 |
71,121 |
5512,589 |
15 |
9200 |
155 |
353,667 |
0,433 |
125080,111 |
0,188 |
153,256 |
16 |
7940 |
115 |
-906,333 |
-39,567 |
821440,111 |
1565,521 |
35860,589 |
17 |
10150 |
221 |
1303,667 |
66,433 |
1699546,778 |
4413,388 |
86606,922 |
18 |
7500 |
103 |
-1346,333 |
-51,567 |
1812613,444 |
2659,121 |
69425,922 |
19 |
8470 |
127 |
-376,333 |
-27,567 |
141626,778 |
759,921 |
10374,256 |
20 |
9010 |
147 |
163,667 |
-7,567 |
26786,778 |
57,254 |
-1238,411 |
21 |
7850 |
123 |
-996,333 |
-31,567 |
992680,111 |
996,454 |
31450,922 |
22 |
10300 |
135 |
1453,667 |
-19,567 |
2113146,778 |
382,854 |
-28443,411 |
23 |
10250 |
165 |
1403,667 |
10,433 |
1970280,111 |
108,854 |
14644,922 |
24 |
9480 |
155 |
633,667 |
0,433 |
401533,444 |
0,188 |
274,589 |
25 |
7700 |
109 |
-1146,333 |
-45,567 |
1314080,111 |
2076,321 |
52234,589 |
26 |
7820 |
107 |
-1026,333 |
-47,567 |
1053360,111 |
2262,588 |
48819,256 |
27 |
8590 |
127 |
-256,333 |
-27,567 |
65706,778 |
759,921 |
7066,256 |
28 |
8040 |
156 |
-806,333 |
1,433 |
650173,444 |
2,054 |
-1155,744 |
29 |
9240 |
150 |
393,667 |
-4,567 |
154973,444 |
20,854 |
-1797,744 |
30 |
7650 |
105 |
-1196,333 |
-49,567 |
1431213,444 |
2456,854 |
59298,256 |
|
265390 |
4637 |
0,000 |
0,000 |
27600696,667 |
69373,367 |
966582,333 |
среднее |
8846,333 |
154,567 |
0,000 |
0,000 |
920023,222 |
2312,446 |
32219,411 |
Gx = 920023,222
Gy = 2312,446
=
0,699,
Значение линейного коэффициента корреляции подтверждает гипотезу о прямой средней связи между стоимостью имущества и прибылью банка.
коэффициент эластичности
Э
= b
= 0,03502
=
2,004
Коэффициент эластичности показывает, что при увеличении стоимости имущества на 1% прибыль банка увеличивается в среднем на 2%;
Задание 4. Рассчитать:
показатели ряда динамики прибыли;
средний уровень прибыли за отчетный год;
средний темп роста;
выровнять ряд динамики по прямой;
определить прогнозное значение прибыли на I квартал следующего года за отчетным.
Исходные данные для расчета
Прибыль банка, млрд. руб. |
|||||||||
3 квартал предыдущего года |
4 квартал предыдущего года |
Базисный год |
Отчетный год |
||||||
I кв. |
II кв. |
III кв. |
IV кв. |
I кв. |
II кв. |
III кв. |
IV кв. |
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
203 |
176 |
221 |
214 |
280 |
199 |
334 |
463 |
180 |
450 |
Решение.
Рассчитаем следующие показатели динамики.
1. Абсолютный прирост
цепной
,
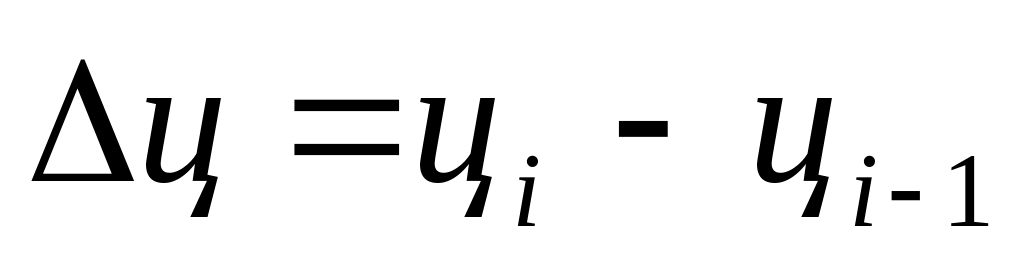где
- уровень ряда;
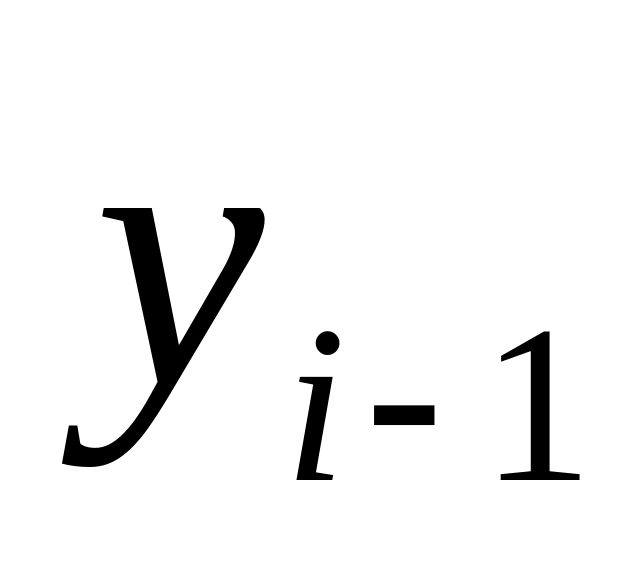- предыдущий уровень рядабазисный
,
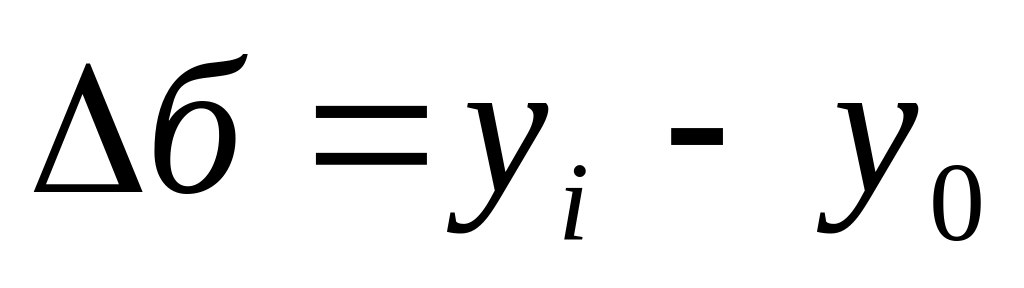где
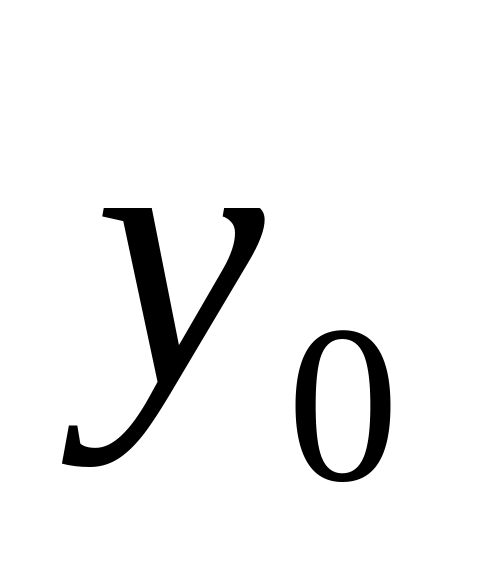- уровень, принятый за базу сравнения
(первоначальный).
2. Темп роста
цепной
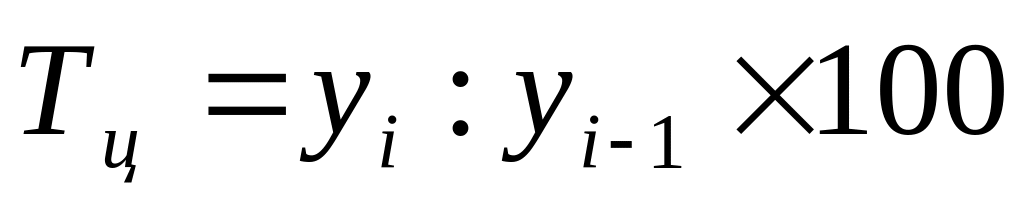;базисный
3. Темп прироста
цепной
базисный
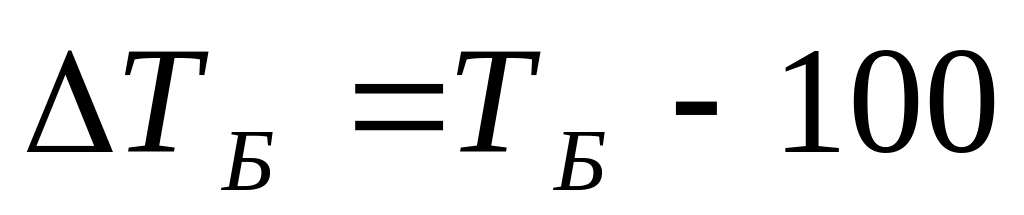
или
,
4. Абсолютное значение одного процента прироста
цепной
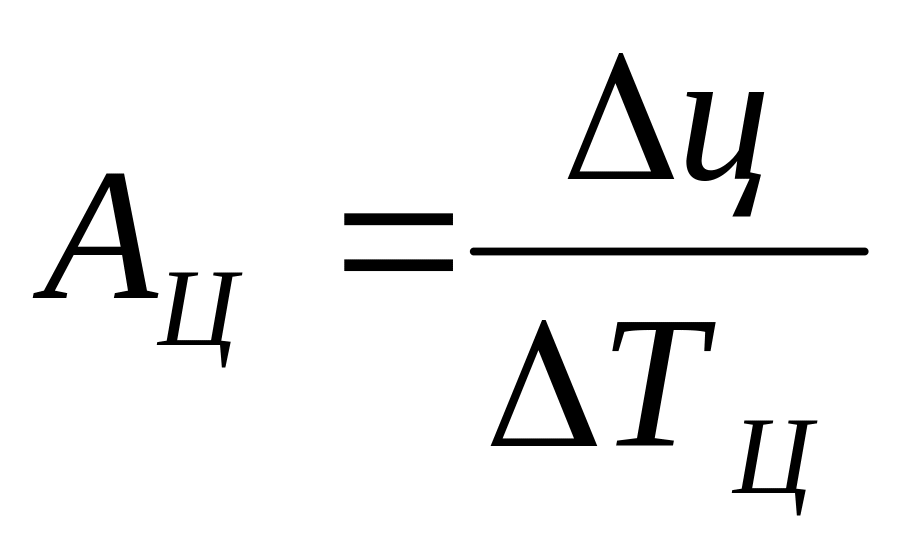
базисный
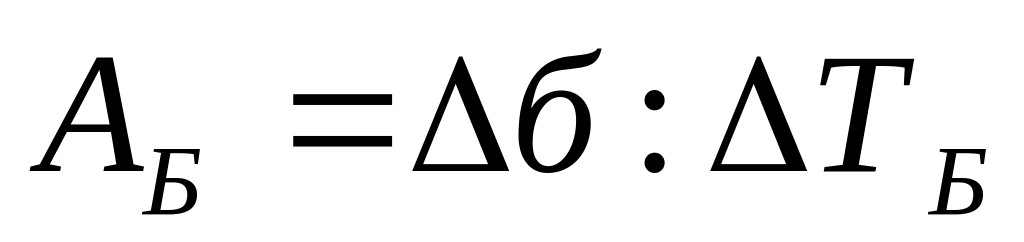
Рассчитаем требуемые показатели для 1 квартала базисного года
1. Абсолютный прирост
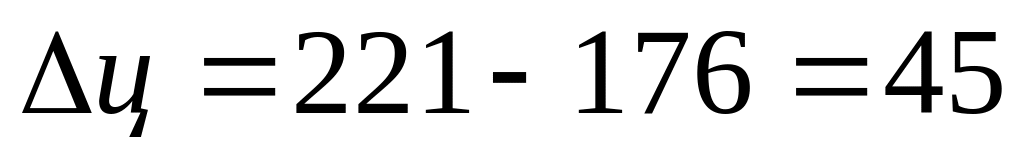млрд.руб.
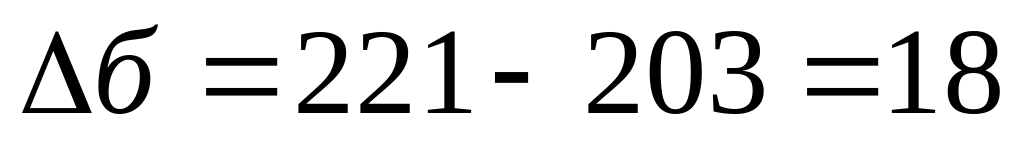млрд.руб.
2. Темп роста
;
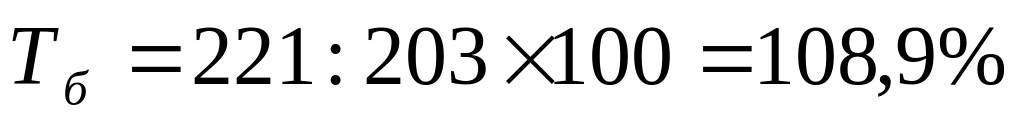
3. Темп прироста
4. Абсолютное значение одного процента прироста
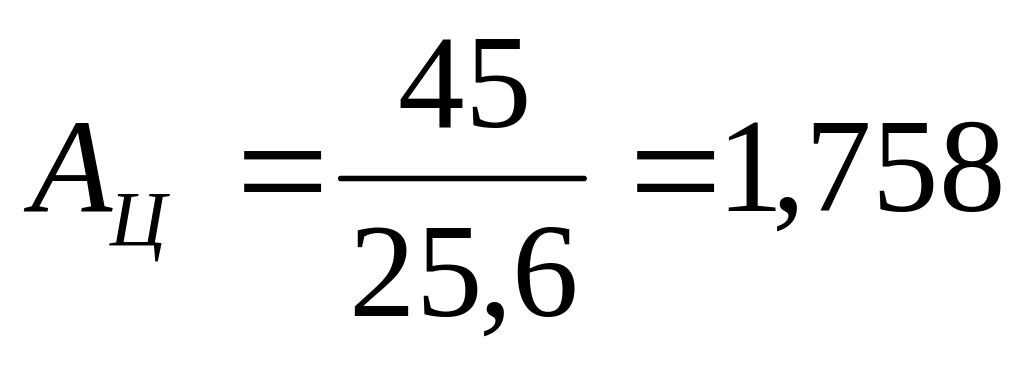млрд.руб.
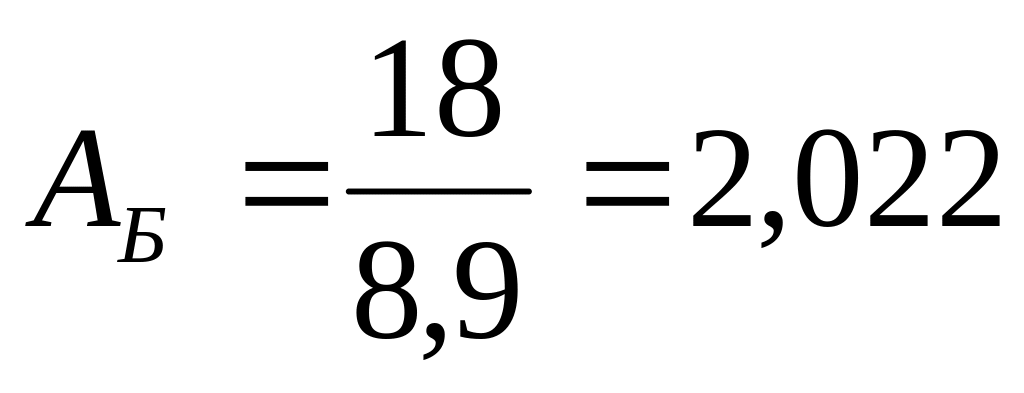млрд.руб.
Аналогично считаем показатели динамики за остальные периоды и представляем в таблице.
Таблица 1 - Цепные и базисные показатели ряда динамики
Пери оды |
Прибыль банка, млрд.руб. |
Абсолютный прирост, руб./чел. |
Темп роста, % |
Темп прироста, % |
Абсолютное значение 1% прироста, млрд.руб. |
||||
цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
||
1 |
203 |
- |
- |
100 |
100 |
- |
- |
- |
- |
2 |
176 |
-27 |
-27 |
86,7 |
86,7 |
-13,3 |
-13,3 |
2,030 |
2,030 |
3 |
221 |
45 |
18 |
125,6 |
108,9 |
25,6 |
8,9 |
1,758 |
2,022 |
4 |
214 |
-7 |
11 |
96,8 |
105,4 |
-3,2 |
5,4 |
2,188 |
2,037 |
5 |
280 |
66 |
77 |
130,8 |
137,9 |
30,8 |
37,9 |
2,143 |
2,032 |
6 |
199 |
-81 |
-4 |
71,1 |
98,0 |
-28,9 |
-2,0 |
2,803 |
2,000 |
7 |
334 |
135 |
131 |
167,8 |
164,5 |
67,8 |
64,5 |
1,991 |
2,031 |
8 |
463 |
129 |
260 |
138,6 |
228,1 |
38,6 |
128,1 |
3,342 |
2,030 |
9 |
180 |
-283 |
-23 |
38,9 |
88,7 |
-61,1 |
-11,3 |
4,632 |
2,035 |
10 |
450 |
270 |
247 |
250,0 |
221,7 |
150,0 |
121,7 |
1,800 |
2,030 |
Средний уровень прибыли за отчетный год рассчитываем о формуле средней арифметической:
млрд.руб.
Средний темп роста за весь представленный будет равен
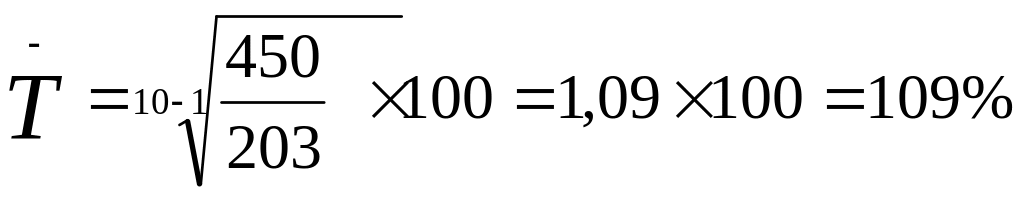
Видим, что средний размер прибыли за отчетный год (4 квартала) равен 356,75 млрд.руб. А средний темп роста за весь период(10 кварталов) составляет 109%.
Для
определения тенденции в развитии
определяют выровненные уровни ряда
(
),
задавая показатель времени t
так, чтобы
,
тогда
,
где
,
.
Расчеты параметров уравнения проведем с помощью таблицы.
Таблица 2 -Расчет параметров уравнения
Периоды |
Прибыль банка, млрд.руб., y |
t |
yt |
t2 |
1 |
203 |
-5 |
-1015 |
25 |
2 |
176 |
-4 |
-704 |
16 |
3 |
221 |
-3 |
-663 |
9 |
4 |
214 |
-2 |
-428 |
4 |
5 |
280 |
-1 |
-280 |
1 |
6 |
199 |
1 |
199 |
1 |
7 |
334 |
2 |
668 |
4 |
8 |
463 |
3 |
1389 |
9 |
9 |
180 |
4 |
720 |
16 |
10 |
450 |
5 |
2250 |
25 |
Итого |
2720 |
0 |
2136 |
110 |
Тогда
млрд.руб.
млрд.руб.
Уравнение прямой имеет вид:
Проставим новые уровни ряда в таблице 3.
Таблица 3 – Выровненные уровни ряда
Периоды |
Прибыль банка, млрд.руб., y |
yt |
1 |
203 |
175 |
2 |
176 |
194,4 |
3 |
221 |
213,8 |
4 |
214 |
233,2 |
5 |
280 |
252,6 |
6 |
199 |
291,4 |
7 |
334 |
310,8 |
8 |
463 |
330,2 |
9 |
180 |
349,6 |
10 |
450 |
369 |
Итого |
2720 |
2720 |
Чтобы
сделать прогноз на следующий период,
необходимо увеличить t
и подставить значение в
.
млрд.руб.
Таким образом, прогнозное значение прибыли на I квартал следующего года за отчетным равно 388,4 млрд.руб.